Complete Solutions to NCERT questions of chapter BEHAVIOUR OF PERFECT GAS & KINETIC THEORY of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | BEHAVIOUR OF PERFECT GAS & KINETIC THEORY |
| PRADEEP | NCERT questions |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
Estimate the fraction of molecular volume to the actual volume occupied by oxygen gas at STP. Take the diameter of an oxygen molecule to be `3 Å`.
View SolutionMolar volume is the volume occupied by 1 mole of any (Ideal) gas at standard temperature and pressure (STP , `0^(@) C`, 1 atmospheric pressure). Show that it is 22.4 litres. Take `R = 8.31 J mol^(-1) K^(-1)`.
View SolutionFig shows of `PV//T` versus P for `1.00 xx 10^(-3) kg` of oxygen gas at two different temperatures.
(a) What does the dotted plot signify ?
(b) Which is true : `T_(1) lt T_(2) or T_(2) lt T_(1) ?`
( c) What is the value of `PV//T` where the curves meet on the Y-axis ?
(d) If we obtained similar plot for `1.00 xx 10^(-3) kg` of hydrogen, would we get the same value of `PV//T` at the point where the curves meet on the y-axis ? If not, what mass of hydrogen yield the same value of `PV//T` (for low pressure high temperature region of the plot) ? (Molecular mass of `H = 2.02 u`, of `O = 32.0 u, R = 8.31 J "mol"^(-1) K^(-1)`
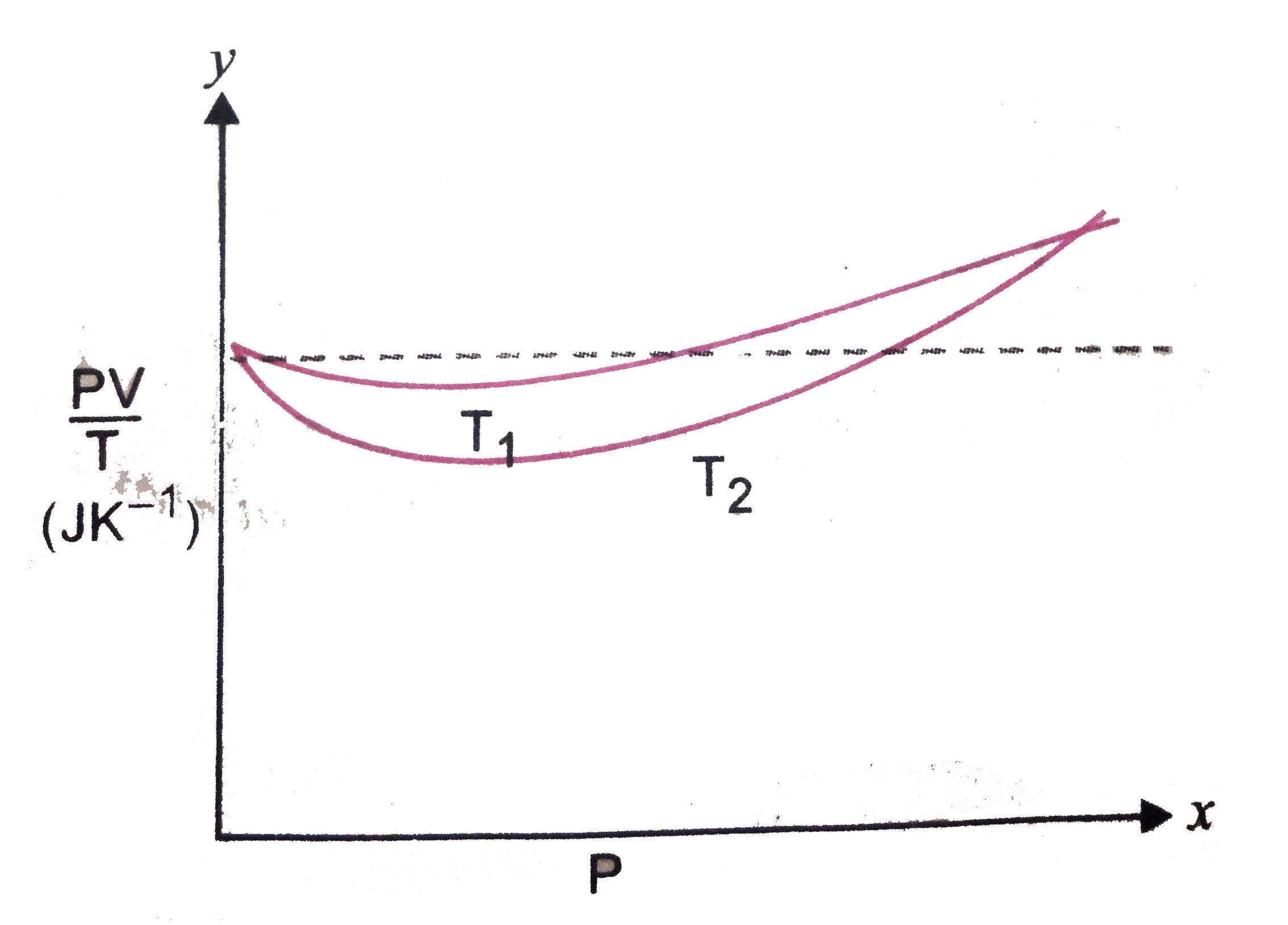
View SolutionAn oxygen cylinder of volume 30 litres has an initial gauge pressure of 15 atm. And a temperature of `27^(@)C`. After some oxygen is withdrawn from the cylinder, the gauge pressure drops to 11 atm. And its temperature drops to `17^(@)C`. Estimate the mass of oxygen taken out of the cylinder. `(R = 8.1 J "mole"^(-1) K^(-1)`, molecular mass of `O_(2) = 32 u)`.
View SolutionAn air bubble of volume `1.0 cm^(3)` rises from the bottom of a take 40 m deep at a temperature of `12^(@) C`. To what volume does it grow when it reaches the surface, which is at a temperature of `35^(@) C`. ? Given `1 atm = 1.01 xx 10^(5) Pa`.
View SolutionEstimate the total number of air molecules (inclusive of oxygen, nitrogen, water vapour and other constituents) in a room of capacity `25.0 m^(3)` at a temperature of `27^(@) C`. And 1 atm pressure. (Boltzmann constant `= 1.38 xx 10^(-23) JK^(-1))`.
View SolutionEstimate the average thermal energy of a helium atom at (i) room temperature `(27^(@)C)` (ii) the temperature on the surface of the sun (6000K), (iii) the temperature of 10 million kelvin (the typical core temperature in the case of a car)
View SolutionThree vessel of equal capacity have gases at the same temperature and pressure. The first vessel contains neon (monoatomic), the second contains chlorine (diatomic), and the third contains uranium hexafluoride (polyatomic). Do the vessels contains equal number of respectice molecules ? Is the root mean square speed of molecules the same in the three cases ? If not, which case is `v_(rms)` the largest?
View SolutionAt what temperature is the root mean square speed of an atom in an argon gas cylinder equal to the r.m.s. speed of a helium gas atom at `-20^(@) C` ? (Atomic mass of Ar = 39.9 u, of He = 4.0 u).
View SolutionEstimate the mean free path and collision frequency of a nitrogen molecule in a cylinder containing nitrogen at 2 atm. And temperature `17^(@)`. Take the radius of a nitrogen molecule to be roughly `1.0 Å`. Compare the collision time with the time molecule moves freely between two successive collisions. (Molecular mass of nitrogen = 28.0 u).
View SolutionA metre long narrow bore held horizontally (and close at one end) contains a `76` cm long mercury thread, which traps a `15` cm column of air. What happens if the tube is held vertically with the open end at the bottom?
View SolutionFrom a certain apparatus, the diffusion rate of hydrogen has an average value of `28.7 cm^(3) s^(-1)`. The diffusion of another gas under the same condition is measured to have an average rate of `7.2 cm^(3) s^(-1)`. Identify the gas.
View SolutionA gas in equilibrium has uniform density and pressure throughout its volume. This is strictly true only if there are no external influences. A gas column under gravity, for example, does not have uniform density (and pressure). As you might expect, its density decreases with height. the precise dependence is given by the so called law of atmosphere' : `n_(2) = n_(1) exp [-mg (h_(2)-h_(1))//k_(B)T]` where, `n_(1). n_(2)` refer to number density at height `h_(1)` and `h_(2)` respectively. use this relation to derive the equation for sedimentation equilibrium of a suspension in a liquid columns:
`n_(2) = n_(1)` exp `[-mg N_(A) (roh-roh^('))(h_(2)-h_(1))//(roh RT)]`
where, `roh` is the density of the suspended particle, and `roh'` that of surrounding medium. `[N_(A)` is Avogadro's number, and `R` is the universal gas constant`]`.
View Solution
NCERT questions questions and complete solutions for chapter BEHAVIOUR OF PERFECT GAS & KINETIC THEORY of PRADEEP PHYSICS (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 PHYSICS BEHAVIOUR OF PERFECT GAS & KINETIC THEORY
- Advance problem for competitions
- Assertion - Reason Type questions
- Conceptual Problems
- Curiosity Question
- Fill in the blanks
- Higher order thinking skills questions
- Integer type questions
- Long answer questions
- Multiple choice questions-I
- Multiple choice questions-II
- Multiple choice questions-III
- NCERT questions
- Problems for practice
- Sample problem
- Short answer questions
- Solved Examples
- Value Based Questions
- Very short Answer questions