Complete Solutions to Exercise-1 (Part-1) of chapter CHEMICAL EQUILIBRIUM of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | CHEMICAL EQUILIBRIUM |
| RESONANCE | Exercise-1 (Part-1) |
| Number Of Questions | 38 |
| Academic Year | 2023-24 |
In a reaction `A+BhArrC+D` the rate constant of forward reaction & backward reaction is `K_(1) and K_(2)` respectively then the equilibrium constant `(K_(C))` for reaction is expressed as
View SolutionWhat is the active mass of `5.6` litres of `O_(2)` at S.T.P.?
View SolutionWrite the expressions for equilbrium constant `K_(c)` and `K_(P)` and classify in Homogeneous and Hetereogeneous equilbrium:
(i) `N_(2)O_(4)(g)hArr2NO_(2)(g)`
(ii) `3Fe(S)+4H_(2)O(g)hArrFe_(3)O_(4)(S)+4H_(2)(g)`
(iii) `NH_(4)HS(S)hArrNH_(3)(g)+H_(2)S(g)`
(iv) ` CH_(3)COOH(f)+C_(2)H_(5)OH(f)hArrCH_(3)COOC_(2)H_(5)(f)+H_(2)O(f)`
(V) `MgCO_(3)(S)hArrMgO(S)+CO_(2))g)`
(vi) `2H_(2)S(g)hArr2H_(2)S(g)hArr2H_(2)(g)+S_(2)(g)`
(vii) `SO_(2)(g)+NO_(2)(g)+NO_(2)(g)hArrSO_(3)(g)+NO(g)`
(viii) ` NH_(4)NO_(2)(S)hArrN_(2)(g)+2H_(2)O(f)`
View SolutionA mixture of `SO_(3), SO_(2)` and `O_(2)` gases is maintained in a `10 L` flask at a temperature at which the equilibrium constant for the reaction is `100`:
`2SO_(2)(g)+O_(2)(g)hArr2SO_(3)(g)`
a. If the number of moles of `SO_(2)` and `SO_(3)` in the flask are equal. How many moles of `O_(2)` are present?
b. If the number of moles of `SO_(3)` in flask is twice the number of moles of `SO_(2)`, how many moles of oxygen are present?
View SolutionThe equilibrium constant of the reaction
`A_(2)(g)+B_(2)(g) hArr 2AB(g)`
at `100^(@)C` is `50`. If a `1L` flask containing `1` mol of `A_(2)` is connected to a `2 L` flask containing `2` mol of `B_(2)`, how many moles of AB will be formed at `373 K`?
View Solutionconsider the given reaction, 3A(g) + B(g) hArr 2C(g) at a given temperature if a mixture of 2 mol each of A, B and C exist at equilibrium and `K_c =9` then volume of the flask will be
View Solution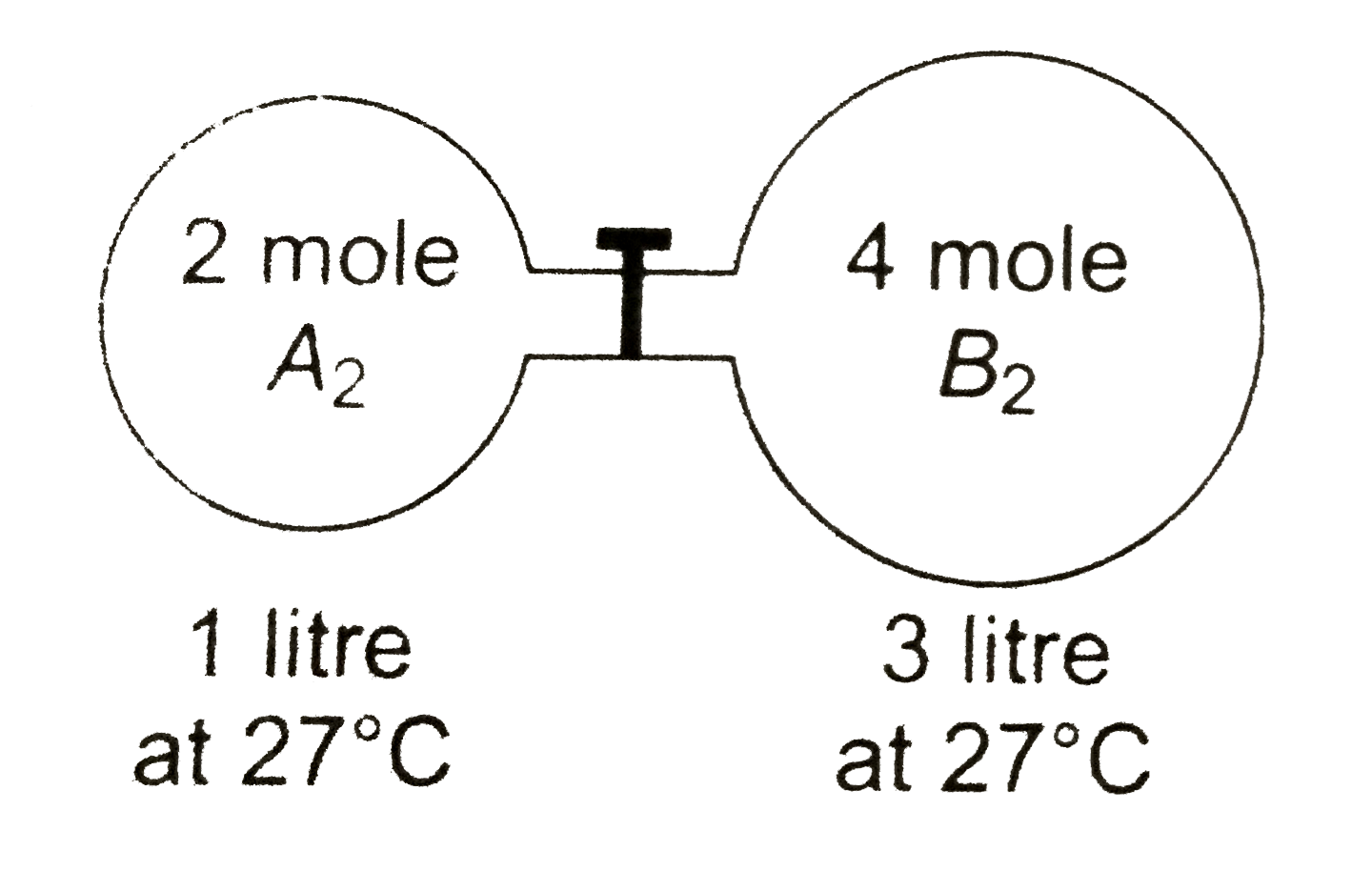
The gas `A_(2)` in the left flask allowed to react with gas `B_(2)` present in right flask as `A_(2)(g)+B_(2)(g)hArr2AB(g),K_(c)=4` at `27^(@)C.` What is the concentration of AB when equilibrium is established ?
View Solutionn mole each of `H_(2)O(g),H_(2)(g) "and" O_(2)(g)` are mixed at a suitable high temperature to attain the equilibrium `2H_(2)O(g)hArr2H_(2)(g)+O_(2)(g)`. If `y` and mole of `H_(2)O(g)` are the dissociated and the total pressure maintained is `P`, calculate the `K_(P)`.
View SolutionThe partial pressures of `N_(2)O_(4) "and" NO_(2) "at" 40^(@)C` for the following equilibrium `N_(2)O_(4)(g)hArr2NO_(2)(g)` are `0.1 "atm and" 0.3` atm respectively. Find `K_(P)` for the reaction.
View Solution`1 "mole of" N_(2) ` and 3 `"moles of " H_(2)` are placed in `1L` vessel. Find the concentration of `NH_(3)` at equilibrium, if the equilibrium constant `(K_(c))` at `400K "is" (4)/(27)`
View SolutionCalculate the expression for `K_(C) "and" K_(P)` if initially a moles of `N_(2) "and" B "moles of" H_(2)` is taken for the following reaction. `N_(2)(g)+3H_(2)(g)hArr2NH_(3)(g) (Deltanlt0)` (P,T,V given)
View Solution`1` mole of a gas `A` is taken in a vessel of volume `1L`. It dissociates according to the reaction
`A(g)hArrB(g)+C(g) "at" 27^(@)C`. Forward and backward reaction rate constants for the reaction are `1.5xx10^(-2) "and" 3xx10^(-2)` respectively. Find the concentrations of `A,B "and" C` at equilibrium.
View Solution`0.15 mol` of `CO` taken in a `2.5 L` flask is maintained at `750 K` alongwith a catalyst so that the following reaction can take place `CO(g)+2H_(2)(g) hArr CH_(3)OH(g)`. Hydrogen is introduced unit the total pressure of the system is 8.5 atm at equilibrium and 0.08 mol of methanol is formed. Calculate
a. `K_(p)` and `K_(c )`
b. The final pressure if the same amount of `CO` and `H_(2)` as brfore is used but no catalyst so that the reaction does not take place.
View SolutionA mixture of `1.57` mol of `N_(2), 1.92` mol of `H_(2)` and `8.13` mol of `NH_(3)` is introduced into a `20 L` reaction vessel at `500 K`. At this temperature, the equilibrium constant, `K_(c)` for the reaction `N_(2)(g) + 3H_(2)(g) hArr 2NH_(3)(g) ` is `1.7 xx 10^(2)`. Is the reaction mixture at equilibrium? If not, what is the direction of the net reaction?
View SolutionAt `460^(@)C, K_(C)=81` for the reaction, `SO_(2)(g)+NO_(2)(g)hArrNO(g)+SO_(3)(g)`
A mixture of these gases has the following concentrations of the reactants and products:
`[SO_(2)]=0.04M [NO_(2)]=0.04m`
`[NO]-0.30m [SO]=0.3m`
Is the system at equilibrium? If not, in which direction must the reaction proceed to reach equilibrium. What will be the molar concentrations of the four gases at equilibrium?
View SolutionFor a reversible reaction, if the concentration of the reactants are doubled, then the equilibrium constant will
View SolutionThe equilibrium constant for the reactions
`N_(2)+O_(2)hArr2NO"and "NO+1/2O_(2)hArrNO_(2)"are"K_(1)"and"K_(2)` respectively, that will be the equilibrium constant for the reaction
View SolutionCalculate the equilibrium constant for the reaction
`H_(2)(g)+CO_(2)(g) hArr H_(2)O(g)+CO(g)` at `1395K`
If the equilibrium constants at `1395 K` for the following are:
`2H_(2)O(g) hArr 2H_(2)+O_(2)(g), K_(1)=2.1xx10^(-13)`
`2CO_(2)(g) hArr 2CO(g)+O_(2)(g), K_(2)=1.4xx10^(-12)`
View SolutionThe homogeneous reversible reaction, `C_(2)H_(5)OH+COOHhArrCH_(3)COOC_(2)H_(5)+H_(2)O` is studied at various initial concentrations of the reactants at constant temperature. Calculate `K` in each case.
`{:(,"Moles of acid", "Moles of alcohol","Moles of ester"),(,"Per litre (initial)","Per litre(initial)","Per litre at equilibrium"),((i),1,1,0.637),((ii),1,4,0.93):}`
View SolutionThe ester ethyl acetate is formed by the reaction of ethanol and acetic acid and the equilibrium is represented as
`CH_3COOH (l) + C_2H_5OH(l) hArr CH_3COOC_2H_5(l) +H_2O (l)`
Write the concentration ratio , Q for this reaction. Note that water is not in excess and is not a solvent in this reactions .
View Solution`N_(2)O_(4)` is 25% dissociated at `37^(@)C` and one atmosphere pressure. Calculate (i) Kp and (ii) the percentage dissociation at 0.1 atm and `37^(@)C` .
View SolutionAt temperature T, a compound `AB_2(g)` dissociates according to the reaction,
`2AB_2(g) hArr 2AB(g) +B_2(g)` with a degree of dissociation, 'x' which is small as compared to unity. The expression for `K_p` in terms of 'x' and total pressure P is
View SolutionVapour density of the equilibrium mixture of `NO_(2)` and `N_(2)O_(4)` is found to be `40` for the equilibrium
`N_(2)O_(4) hArr 2NO_(2)`
Calculate
View SolutionWhen sulphur in the form of `S_(8)` is heated at `900 K`, the initial pressure of `1` atm falls by `10%` at equilibrium. This is because of conversion of some `S_(8)` to `S_(2)`. Find the value of equilibrium constant for this reaction.
View SolutionIn a container `H_(2)O(g),CO(g) "and" H_(2)(g)` are present in the molar ration of `1:2:3` respectively at temperature of `300K`, Find the pressure in the container at which solid carbon (graphile) will star forming in the container given that:
`C(S)+H_(2)O(G)hArrCO(g)+H_(2)(g) K_(p)=3` atm
View Solution`K_(p) "is" atm^(2)` for the reaction: `LiCI.3NH_(3)(s)hArrLiCI.NH_(3)(s)+2NH_(3)(g) "at" 40^(@)C`. How many moles of ammonia must be added at this temperature to a `5` litre flask containing `0.1` mole of LiCI. `NH_(3)` in order to completely convert the solid to `LiCI.3NH_(3)`?
View SolutionEquilibrium constant for the following equilibrium is given at `0^(@)C` . `Na_(2)HPO_(4)` . `12H_(2)O(s) hArrNa_(2)HPO_(4)` . `7H_(2)O(s) + 5H_(2)O(g)` `K_(p) = 31.25xx10^(-13)`. At equilibrium what will be partial pressure of water vapour:
View SolutionEquilibrium constant for the following equilibrium is given at `0^(@)C` . `Na_(2)HPO_(4)` . `12H_(2)O(s) hArrNa_(2)HPO_(4)` . `7H_(2)O(s) + 5H_(2)O(g)` `K_(p) = 31.25xx10^(-13)`. At equilibrium what will be partial pressure of water vapour:
View SolutionThe dissociation pressure of silver oxide at `445^(@)C "is" 207` atm. Calculate `DeltaG^(@)` for the formation of `1` mole `Ag_(2)O(S)` from metal and oxygen at this temperature. (`"log" 207=2.315`)
View SolutionGiven below are the values of `DeltaH^(ɵ)` and `DeltaS^(ɵ)` for the reaction given below at `27^(@)C`.
`SO_(2)(g)+1/2O_(2)(g) rarr SO_(3)(g)`
`DeltaH^(ɵ)=-98.32 kJ mol^(-1), DeltaS^(ɵ)=-95 J mol^(-1)`
Find `K_(p)` for the reaction
View SolutionFrom the following data
i. `H_(2)(g)+CO_(2)(g) hArr H_(2)O(g)+CO(g), K_(2000 K)=4.40`
ii. `2H_(2)O(g) hArr 2H_(2)(g)+O_(2)(g), K_(2000 K)^(I)=5.31xx10^(-10)`
iii. `2CO(g)+O_(2)(g) hArr 2CO_(2)(g), K_(1000 K)=2.24xx10^(22)`
Show whether reaction (iii) is exothermic or endothermic.
View SolutionTell whether reaction will get affected by increase of pressure? Also mention, whether change will cause the reaction to go into
the right or left direction?
`C_(2)H_(4(g))+H_(2(g))hArrC_(2)H_(6(g))`
View SolutionUsing "Le" Chateller's principle, predict the effect of
(i) decreasing the temperature and
(ii) increasing the pressure on each of the following equilibria:
(A) `N_(2)(g)+3H_(2)(g)hArr2NH_(3)(g)+"Heat"`
(B) `N_(2)(g)+O_(2)(g)hArr2NO(g)+"Heat"`
(C) `H_(2)O(g)+"Heat"hArrH_(2)(g)+(1)/(2)O_(2)(g)`
(D) `2CO(g)+O_(2)(g)hArr2CO_(2)(g)+"Heat"`
View SolutionThe decomposition of solid ammonium carbamate, `(NH_(4))(NH_(2)CO_(2))`, to gaseous ammonia and carbon dioxide is an endothermic reaction.
`9NH_(4))(NH_(2)CO_(2)))(s)hArr2NH_(3)(g)+CO_(2)(g)`
(a) When solid `(NH_(4))(NH_(2)CO_(2))` is introduced into and evacuated flask at `25^(@)C`, the total pressure of gas at equilibrium is `0.3` atm. What is the value of `K_(p) "at" 25^(@)C`?
View SolutionFollowing equilibrium is established at temperature T.
`A(g)hArrB(g)+C(g`)
at eq. `1M 2 M 2M`.
If volume of the vessel is doubled then find the equilibrium concentration of each species. (Given that : `sqrt40=6.324)`
View SolutionTwo solid compounds A and B dissociate into gaseous products at `20^(@)C` as
a. `A(s) hArr A'(s)+H_(2)S(g)`
b. `B(s) hArr B'(g)+H_(2)S(g)`
At `20^(@)C` pressure over excess solid A is `50` mm and that over excess solid B is `68` mm. Find:
a. The dissociation constant of A and B
b. Relative number of moles of A' and B' in the vapour phase over a mixture of the solids A and B.
c. Show that the total pressure of gas over the solid mixture would be `84.4` mm.
View SolutionIn a vessel, two equilibrium are simultanceously established at the same temperature as follows:
`N_(2)(g)+3H_(2)(g)hArr2 NH_(3)(g)`.... (1)
`N_(2)g)+2H_(2)(g)hARrN_(2)H_(4)(g)` ....(2)
Initially the vessel contains `N_(2) "and" H_(2)` in the molar ratio of `9:13`. The equilibrium pressure is `7P_(0)`, in wich pressure due to ammonia is `P_(o)` and due to hydrogen is `2P_(0)`. Find the values of equilibrium constats `(K_(p)'S)` for both the reactions
View SolutionWhen `NO` and `NO_(2)` are mixed, the following equilibria are readily obtained,
`2NO_(2) hArr N_(2)O_(4), K_(p)=6.8 atm^(-1)`
`NO+NO_(2) hArr N_(2)O_(3)`
In an experiment when `NO` and `NO_(2)` are mixed in the ratio of `1:2`, the final total pressure was `5.05` atm and the partial pressure of `N_(2)O_(4)` was `1.7` atm. Calculate
a. the equilibrium partial pressure of `NO`.
b. `K_(p)` for `NO+NO_(2) hArr N_(2)O_(3)`.
View Solution
Exercise-1 (Part-1) questions and complete solutions for chapter CHEMICAL EQUILIBRIUM of RESONANCE ENGLISH of Class 11
All Exercises from RESONANCE Class 11 CHEMISTRY CHEMICAL EQUILIBRIUM
- (MSPs)
- Advanced Level Problems (Part-1)
- Advanced Level Problems (Part-2)(Section-1)
- Advanced Level Problems (Part-2)(Section-2)
- Advanced Level Problems (Part-2)(Section-3)
- Advanced Level Problems (Part-3)(Stage-1)
- Advanced Level Problems (Part-3)(Stage-2)
- Advanced Level Problems (Part-3)(Stage-5)
- Board Level Exercise
- Exercise-1 (Part-1)
- Exercise-1 (Part-2)
- Exercise-2 (Part-1)
- Exercise-2 (Part-2)
- Exercise-2 (Part-3)
- Exercise-2 (Part-4)
- Exercise-3 (Part-1)
- Exercise-3 (Part-2)
- INORGANIC CHEMISTRY(Metallurgy)
- ORGANIC CHEMISTRY(Alkyl Halide, Alcohol,Phenol,Ether)
- PHYSICAL CHMISTRY (CHMICAL EQUILIBRIUM)
- Solved examples