Complete Solutions to Exercise-1 (Part-2) of chapter CHEMICAL EQUILIBRIUM of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | CHEMICAL EQUILIBRIUM |
| RESONANCE | Exercise-1 (Part-2) |
| Number Of Questions | 87 |
| Academic Year | 2023-24 |
A reversible reaction is one which :
View SolutionIf a chemical reaction is at equilibrium, it means that:
View SolutionMolar concentration of 96 g of `O_(2)` contained in a 2 L vessel is:
View SolutionRate of reaction curve for equilibrium can be like: `[r_(f)=` forward rate, `r_(b) =` backward rate]
View SolutionThe active mass of `64 g` of `HI` in a `2-L` flask would be
View SolutionThe active mass of `64 g` of `HI` in a `2-L` flask would be
View Solution
Initially the reactions in the container `a "&" b` are at equilibrium when the products & reactants are put together in a container `C` then at the equilibrium the total number of different compounds are-
View SolutionActive mass of a `6%` solution of a compound is `2` then calculate
molar mass of compound.
View SolutionIn a reversible reaction `Aunderset(K_2)overset(K_1)hArrB` the initial concentration of A and B are a and b in moles per litre and the equilibrium concentrations are (a-x) and (b+x) respectively, Express x in terms of `K_1, K_2, a and b`.
View SolutionThe reaction `A + B hArr C + D` is studied in a one litre vessel at `250^(@)C` . The initial concentration of A was 3n and that of B was n. When equilibrium was attained, equilibrium concentration of C was found to the equal to the equilibrium concentration of B. What is the concentration of D at equilibrium ?
View SolutionThe figure shows the change in concentration of species A and B as a function of time.
The equilibrium constant `K_(c)`for the reaction` A(g)hArr2B(g)` is :

View SolutionUsing moler concentrations, what is the unit of `K_(c)` for the reaction ?
`CH_(3)OH(g)hArrCO(g)+2H_(2)(g)`
View Solution`K_(c) = 9` for the reaction, `A + B hArrC + D`. If A and B are taken in equal amounts, then amount of C in equilibrium is:
View SolutionThe equilibrium `N_(2) (g) + O_(2) (g)hArr 2NO (g)` is established in a reaction vessel of `2.5` L capacity. The amounts of `N_(2)` and `O_(2)` taken at the start were respectively 2 moles and 4 moles. Half a mole of nitrogen has been used up at equilibrium. The molar concentration of nitric oxide is:
View SolutionAn equilibrium mixture for the reaction
`2H_(2)S(g) hArr 2H_(2)(g) + S_(2)(g)`
had 1 mole of `H_(2)S, 0.2` mole of `H_(2)` and 0.8 mole of `S_(2)` in a 2 litre
flask. The value of `K_(c)` in mol `L^(-1)` is
View SolutionWhat is the unit of `K_(p)` for the reaction ?
`CS_(2)(g)+4H_(2)(g)hArrCH_(4)(g)+2H_(2)S(g)`
View Solution`N_2 and H_2` are taken in 1:3 molar ratio in a closed vessel to attained the following equilibrium , `N_2(g)+3H_2(g) hArr 2NH_3(g)`
Find `K_p` for reaction at total pressure of 2P if `P_(N_2)` at equilibrium is `P/3`:
View SolutionThe equilibrium constant, `K_(p)` for the reaction
`2SO_(2)(g)+O_(2)(g)hArr2SO_(3)(g)`
is `44.0atm^(-1) "at" 1000 K`. What would be the partial pressure of `O_(2)` if at equilibrium the amound of `SO_(2)` and `SO_(3)` is the same?
View SolutionFor the reaction `A_(2)(g) + 2B_(2)hArr2C_(2)(g)` the partial pressure of
`A_(2)` and `B_(2)` at equilibrium are `0.80` atm and `0.40` atm respectively.
The pressure of the system is `2.80` atm.
The equilibrium constant `K_(p)` will be
View Solution`PCl_(5)hArrPCl_(3)+Cl_(2)` in the reversible reaction the moles of `PCl_(5).PCl_(3)` and `Cl_(2)` are a,b and c respectively and total pressure is `P` then value of `K_(p)` will be
View SolutionAt 1000 K , a sample of pure `NO_(2)` gases decomposes as :
`2NO_(2)(g)hArr2NO(g)+O_(2)(g)`
The equilibrium constant `K_(P)` is 156.25 atm .Analysis showns that the partial pressure of `O_(2)` is 0.25 atm at equilibrium .The parital pressure o f`NO_(2)` at equilibrium is :
View Solution10 lt. box contain `O_3 and O_2` at equilibrium at 2000 K.The `DeltaG^**=-534.52 kJ` at 8 atm equilibrium pressure The following equilibrium is present in the container
`2O_3(g)hArr3O_2(g)`.The partial pressure of `O_3` will be (In 10=2.3, R=8.3 J`"mole"^(-1)K^(-1)`):
View SolutionAt `527^(@)C`, the reaction given below has`K_(c)=4`
`NH_(3)(g)hArr(1)/(2)N_(2)(g)+(3)/(2)H_(2)(g)`
what is the `K_(p)` for the reaction ?
`N_(2)(g)+3H_(2)(g)hArr2NH_(3)(g)`
View SolutionThe value of `K_(p)` fot the reaction `2H_(2)O(g) + 2Cl_(2)(g)hArr4HCl(g) + O_(2)(g)` is `0.03` and at
`427^(@)C`, when the partial pressure are expressed in atmosphere
then the value of `K_(c)` for the same reaction is:
View Solutionlog `K_p/K_c`+log RT=0 is a relationship for the reaction :
View SolutionFor the following gases equilibrium, `N_(2)O_(4) (g)hArr2NO_(2) (g)` , `K_(p)` is found to be equal to `K_(c)`. This is attained when:
View Solutionconsider the following reversible gaseous reaction (at 298 K):
`(A) N_(2)O_(4)hArr` `2NO_2` (B) `2SO_(2) + O_(2)hArr2SO_(3)`
(C) `2HI hArrH_(2) + I_(2)` (D) `X + Y hArr4Z `
Highest and lowest value of `(K_(p))/(K_(c))` will be shown by the equilibrium
View Solution2 moles each of `SO_(3)`, CO, `SO_(2)` and `CO_(2)` is taken in a 1 L vessel. If `K_(C)` for `SO_(3) + COhArrSO_(2) + CO_(2)` is `1//9` then:
View SolutionIn a reaction mixture containing `H_(2),N_(2)` and `NH_(3)` at partial pressure of 2 atm, 1 atm and 3 atm respectively, the value of `K_(p)` at `725K` is `4.28xx10^(-5)atm^(-2)` . In which direction the net reaction will go ?
`N_(2)(g)+3H_(2)(g)hArr 2NH_(3)(g)`
View SolutionFor the equilibrium `CH_(3)-CH_(2)-CH_(2)-CH_(3)(g)hArrCH_(3)-overset(CH_(3))overset(|)underset(H)underset(|)(C)-CH_(3)(g)` equilibrium constant is found to be `1.732` at `298K`. Now if in a vessel at `298K`, a mixture of these two gases be taken as represented by the point `P` in the figure, predict what will hapen

View SolutionThe reaction quotient (Q) for the reaction, `N_2(g) +3H_2(g) hArr2NH_3(g)` is given by `Q=([NH_3]^2)/([N_2][H_2]^3)` The reaction will proceed towards rigt side, if
View SolutionFor the reaction `:` `" "2A+B hArr 3C` at `298 K, K_(c)=49`
A `3L` vessel contains 2,1 and 3 molesof `A, B` and `C` respectively.
The reaction at the same temperature
View SolutionWhen two reactants A and B are mixed to give products C and D, the reaction quotient Q at the initial stages of the reaction
View SolutionAt a certain temperature , the following reactions have the equilibrium constants as shown below:
`S(s)+O_(2)(g)hArrSO_(2)(g),K_(c)=5xx10^(52)`
`2S(s)+3O_(2)(g)hArr2SO_(3)(g),K_(c)=10^(29)`
what is the equilibrium constant `K_(c)`for the reaction at tahea same temperature?
`2SO_(2)(g)+O_(2)(g)hArr2SO_(3)(g)`
View SolutionThe equilibrium constant of the reaction `SO_(2)(g) + 1//2O_(2)(g)hArrSO_(3)(g)` is `4xx10^(-3)atm^(-1//2)`. The equilibrium constant of the reaction
`2SO_(3)(g)hArr2SO_(2)(g) + O_(2)(g)` would be:
View SolutionEquilibrium constant for the reactions,
`2 NO+O_(2)hArr2 NO_(2) "is" K_(c_(1)`,
`NO_(2)+SO_(2)hArrSO_(3)+NO "is" L_(C_(2)` and
`2 SO_(3)hArr2 SO_(2)+O_(2) "is" K_(c_(3)` then correct reaction is:
View SolutionFor a container contining `A(g),B(g),C(g) "&" D(g)` with rigid walls, an experiment is carried upon. This experiment involves increase in temperature of container in stepsof `1^(@)C` and system is allowed to attain equilibrium, followed by calculation of `K_(1) "&" K_(2)` at each step, where `K_(1) "&" K_(2)` are equilibrium constants for reaction (1) & (2) respectively.
`A(g)+2B(g)hArrC(g)+D(g)` ....(1)
`C(g)+D(g)hArrA(g)+2B(g)` .....(2)
Select the graph showing correct relationship-
View SolutionThe equilibrium constant for `N_(2)(g)+O_(2)(g)hArr2NO "is" K_(1)`
and that for `NO(g)hArr(1)/(2)N_(2)(g)+(1)/(2)O_(2)(g)` is `K_(2). K_(1) "and" K_(2)`
will be related as
View SolutionWhen alcohol `(C_(2)H_(5)OH(l)) "and acetic acid" (CH_(3)COOH(l))` are mixed together in equimolar ratio at `27^(@)C,33%` of each is converted into ester. Then the `K_(c)` for the equilibrium
`C_(2)H_(5)OH(l)+CH_(3)COOH(l)hArrCH_(3)COOC_(2)H_(5)(l)+H_(2)O(l)`is:
View SolutionOne litre of 2 M acetic acid and one litre of 3 M ethyl alcohol are mixed to form ester according to the given equation: `CH_(3)COOH+C_(2)H_(5)OH hArr CH_(3)COOC_(2)H_(5)+H_(2)O` If each solution is diluted by adding equal volume (1 litre) of water by how many times the initial forward rate has changed?
View SolutionWhen `alpha-D` glucose is dissolved in water, it undergoes a partial converion to `beta-D` glucose to exhibit mutarotation. This conversion stops when `63.6%` of glucose is in `beta` form. Assuming that equilibrium has been attained, calculate `K_(c)` for mutarotation.
View SolutionFor the dissociation reaction `N_(2)O_(4) (g)hArr 2NO_(2)(g)`, the degree of dissociation `(alpha)`interms of `K_(p)` and total equilibrium pressure P is:
View SolutionThe degree of dissociation of `SO_(3)` is `alpha` at equilibrium pressure `P_(0)`.
`K_(P)` for `2SO_(3)(g)hArr2SO_(2)(g)+O_(2)(g)`is
View SolutionIn the dissociation of `N_(2)O_(4)` into `NO_(2), (1+ alpha)` values with the vapour densities ratio `((D)/(d))` is given by: [`alpha` degree of dissociation, D-vapour density before dissociation, d-vapour density after dissociation]
View Solution`N_2O_4rarr2NO_2`
In the above equation, `alpha` varies with `(D)/(d)` according to:
View SolutionFor the reaction `N_2O_4 hArr 2NO_2(g)`, if percentage dissociation of `N_2O_4` are 20%, 45%, 65%, 80% then the sequence of observed vapour densities wil be :
View SolutionAt a certain temperature `T`, a compound `AB_(4)(g)` dissociates as
`2AB_(4)(g)hArrA_(2)(g)+4B_(2)(g)`
with a degree of dissociation `alpha`, which compared to unity. The expressio of `K_(P)` in terms of `alpha` and total pressure `P` is:
View SolutionThe degree of dissociation of `PCl_(5)(g)` for the equilibrium `PCl_(5)(g)hArrPCl_(3)(g)+Cl_(2)(g)` is approximately releated to the pressure at equilibrium (P) by the relation `[altlt1]`
View SolutionAt `727^(@)C` and `1.2 atm` of total equilibrium pressure, `SO_(3)` is partially dissociated into `SO_(2)` and `O_(2)` as:
`SO_(3)(g)hArrSO_(2)(g)+(1)/(2)O_(2)(g)`
The density of equilibrium mixture is `0.9 g//L`. The degree of dissociation is:, `[Use R=0.08 atm L mol^(-1) K^(-1)]`
View SolutionConsider the following hypothetical equilibrium
`2B(g)hArrB_(2)(g)`
If `d` is observed vapour density and `D` is theoretical vapour density, then degree of association `(alpha)` will be
View SolutionThe vapour density of fully dissociated `NH_(4)Cl` would be
View SolutionThe degree of dissociation is `0.5 at 800K and 2` atm for the gaseous reaction
`PCl_(5)hArrPCl_(3)+Cl_(2)`
Assuming ideal behaviour of all the gases.
Calculate the density of equilibrium mixture at `800K "and" 2` atm.
View Solution`SO_(3)(g)hArrSO_(2)(g)+(1)/(2)O_(2)(g)`
If observed vapour density of mixture at equilibrium is `35` then find out value of `alpha`
View SolutionWhat is the minimum mass of `CaCO_3(s)`, below which it decomposes completely, required to establish equilibrium in a 6.50 litre container for the reaction : `[K^@=0.05` mole/litre]
`CaCO_3(s)hArrCaO(s)+CO_2(g)`
View SolutionIf 50% of `CO_(2)` converts to CO at the following equilibrium:
`(1)/(2)C(s)+(1)/(2)CO_(2)(g) iff CO(g)`
and the equilibrium pressure is 12 atm. Calculate `K_(P)`.
View SolutionSolid ammonium carbamate dissociate to give ammonia and carbon dioxide as follows
`NH_(2)COONH_(4)(s)hArr2NH_(3)(g)+CO_(2)(g)`
which of the following graph correctly represents the equilibrium.
View SolutionFor `NH_(4)HS(s)hArrNH_(3)(g)+H_(2)S(g)` reaction started only with `NH_(4)HS(s)`, the observed pressure for reaction mixture in equilibrium is `1.2` atm at `106^(@)C`. What is the value of `K_(p)` for the reaction?
View SolutionConsider the decomposition of solid `NH_(4)HS` in a flask containing `NH_(3)(g)` at a pressure of `2` atm. What will be the partial pressure of `NH_(3)(g) "and" H_(2)S(g)` after the equilibrium has been attained?
`K_(p)` for the reaction is `3`.
View SolutionWhat is the relative humidity of air at `1` bar pressure and `313K` temperature if partial pressure of water is `19.355` mmHg. For any data use the table given below:

View SolutionFor the equilibrium `CuSO_(4)xx5H_(2)O(s)hArrCuSO_(4)xx3H_(2)O(s) + 2H_(2)O(g)`
`K_(p) = 2.25xx10^(-4)atm^(2)` and vapour pressure of water is `22.8` torr at 298 K. `CuSO_(4)` . `5H_(2)O(s)` is efflorescent (i.e., losses water) when relative humidity is :
View Solution(a) `CuSO_(4).5H_(2)O(s)hArrCuSO_(4).3H_(2)O(s)+2H_(2)O(g) K_(p)=4xx10^(-4)atm^(2)`
(b) `Na_(2)SO_(4).10H_(2)O(s)hArrNa_(2)SO_(4).5H_(2)O(s)+5H_(2)O(g) K_(p)=2.43xx10^(-8) atm^(5)`
(c) `Na_(2)S_(2)O_(3).5H_(2)O(s)hArrNa_(2)S_(2)O_(3).2H_(2)O(s)+3H_(2)O(g) K_(p)=6.4xx10^(-5) atm^(3)`
What is order of vapour pressure and relative humidity respectively.
View SolutionFor the equilibrium `CuSO_(2).5H_(2)O(s)hArrCuSO_(4).3H_(2)O(s)+2H_(2)O(g)`
`K_(p)=2.25xx10^(-4)atm^(2)` and vapour pressure of water is `22.8 "Torr at" 298K`.
`CuSO_(4).5H_(2)O(s)` is efforescent (i.e., loses water) when relative humidity is:
View Solution`CuSO_(4).5H_(2)O(s)hArrCuSO_(4). 3H_(2)O(s)+2H_(2)O(g), K_(p)=4xx10^(-4)atm^(2)` If the vapour pressure of water is 38 toor then percentage of relatative humidity is :(Assume all data at constant temperture)
View SolutionThe correct relationship between free energy change in a reaction and the corresponding equilibrium constant, `K_(c)` is
View SolutionFor the reaction, `H_(2)(g)+I_(2)(g)hArr 2HI(g), K_(c)^(@)=66.9` at `350^(@)C` and `K_(c)^(@)=50.0` at `448^(@)C`. The reaction has
View SolutionThe equilibrium constants for the reaction `Br_(2)hArr 2Br`
at 500 K and 700 K are `1xx10^(-10)` and `1xx10^(-5)` respectively. The reaction is:
View SolutionAn exothermic reaction is represented by the graph :
View SolutionAn endothermic reaction is represented by the graph:
View SolutionThe value of `DeltaG^(@)` for a reaction in aqueous phase having `K_(c)=1,` would be :
View SolutionThe effect of temperature on equilibrium constant is expressed as`(T_(2)gtT_(1))`
log`K_(2)//K_(1)=(-DeltaH)/(2.303)[(1)/(T_(2))-(1)/(T_(1))]`. For endothermic, false statement is
View SolutionFor the reaction
`CO(g)+H_(2)O(g) hArr CO_(2)(g)+H_(2)(g)`
at a given temperature, the equilibrium amount of `CO_(2)(g)` can be increased by
View SolutionGiven the following reaction at equilibrium `N_(2)(g) + 3H_(2)(g)hArr2NH_(3)(g)`. Some inert gas at constant pressure is added to the system. Predict the following facts:
View SolutionThe equilibrium `SO_(2)Cl_(2)(g) hArr SO_(2)(g)+Cl_(2)(g)` is attained at `25^(@)C` in a closed container and an inert gas, helium, is introduced. Which of the following statement is`//`are correct?
View SolutionDensities of diamond and graphite are `(3.5g)/(mL)` and `(2.3g)/(mL)`.
C (diamond) equilibrium C (graphite)
`Delta_(7)H=-1.9(kJ)/("mole")`
Favourable conditions for formation of diamond are:
View SolutionIntroduction of inert gas (at the same temperature) will affect the equilibrium if :
View SolutionThe equilibrium `SO_(2)Cl_(2)(g) hArr SO_(2)(g)+Cl_(2)(g)` is attained at `25^(@)C` in a closed container and an inert gas, helium, is introduced. Which of the following statement is`//`are correct?
View SolutionAn equilibrium mixture in a vessel of capacity `100` litre contain `1 "mol" N_(2).2"mol"O_(2) "and" 3 "mol" NO`. Number of moles of `O_(2)` to be added so that at new equilibrium the conc. Of `NO` is found to be `0.04` mol//lt.
View SolutionFor an equilibrium `H_(2)O(s)hArrH_(2)O(l),` which of the following statements is ture ?
View SolutionA reaction in equilibrium is respresnt by the following equation `2A_((s)) + 3B_((g))hArr3C_((g)) + D_((g)) + O_(2(g))` if the pressure on the system is reduced to half of its original value
View SolutionFor the reaction
`CO(g)+H_(2)O(g) hArr CO_(2)(g)+H_(2)(g)`
at a given temperature, the equilibrium amount of `CO_(2)(g)` can be increased by
View SolutionThe two equilibrium `AB hArr A^(+) + B^(-) and AB+B^(-)hArrAB_(2)^(-)` are simultaneously maintained in a solutio with equilibrium constant `K_(1) and K_(2)` respectively. The ratio of `[A^(+)] ` to `[AB_(2)^(-)]` in the solution is
View SolutionIn the preceeding problem, if`[A^(+)]"and"[AB_(2)^(-)] "are " y " and " x` respectively, under equilibrium produced by adding the substance `AB` to the solvents, then `K_(1)/K_(2) "is equal to"`
View SolutionThe following two reactions:
i. `PCl_(5)(g) hArr PCl_(3)(g)+Cl_(2)(g)`
(ii) `COCl_(2)(g) hArr CO(g)+Cl_(2)(g)`
are simultaneously in equilibrium in a container at constant volume. A few moles of `CO(g)` are later introduced into the vessel. After some time, the new equilibrium concentration of
View Solution`C(s)+CO_(2)(g)hArr2CO(g) K_(p)=1atm`
`CaCO_(3)(s)hArrCaO(s)+CO_(2)(s) K_(p)=4xx10^(-2)`
Solid `C,CaO "and" CaCO_(3) "are mixed and allowed to attain equilibrium. Calculate final pressure of" CO`.
View Solution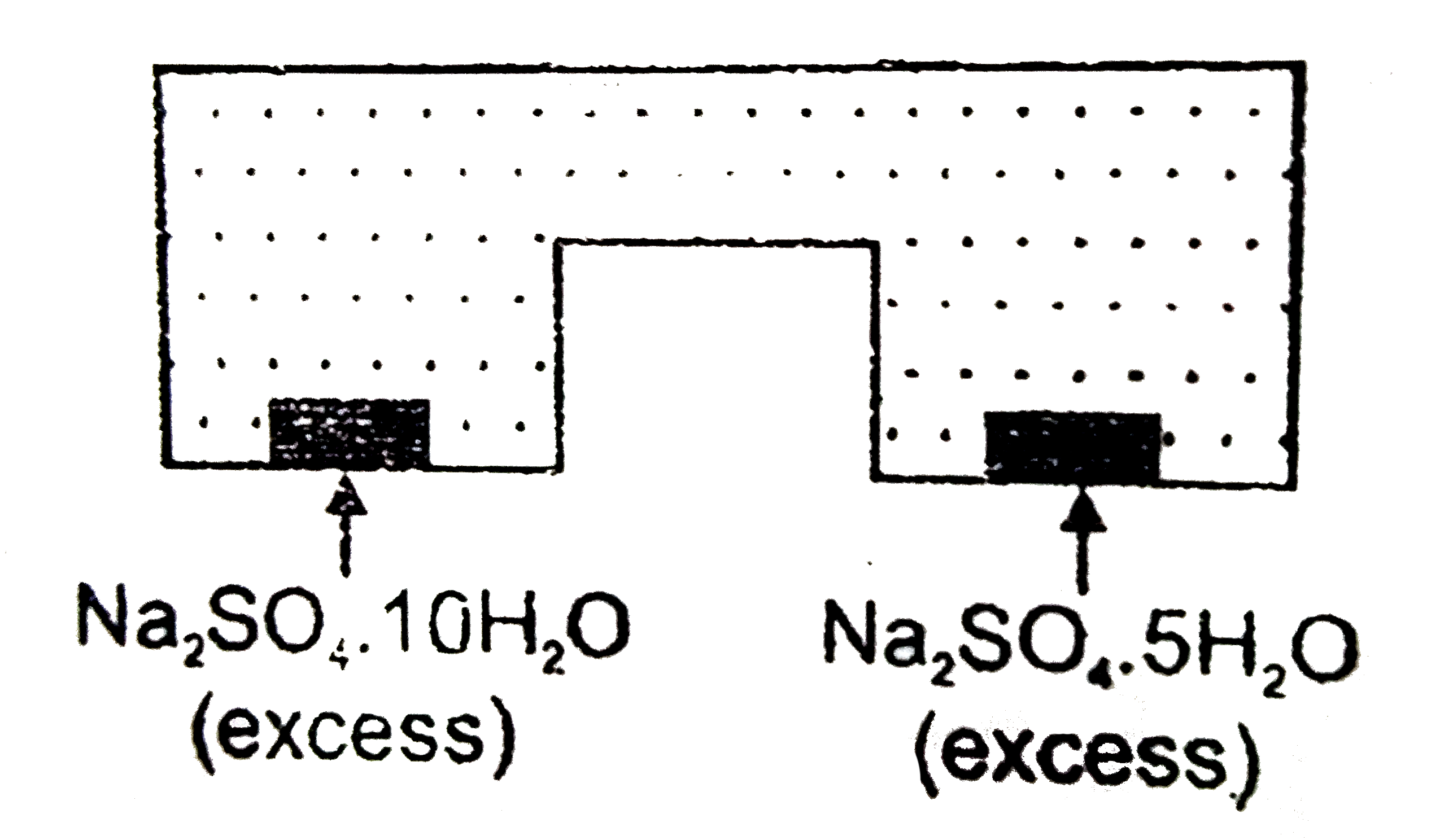
`Na_(2)SO_(4).10H_(2)O(s)hArrNa_(2)SO_(4).5H_(2)O(g) K_(P)=2.43xx10^(-8)` atm^(5) incorrect statement is-
View Solution`A(s)hArrB(g)+C(g) K_(p_(1))=36 atm^(2)`
`E(s)hArrB(g)+D(g) K_(p_(2))=64atm^(2)`
Both solids `A "&" E` were taken in a container of constant volume at a give temperature. Total pressure in the container after equilibrium is
View SolutionIn a closed container following equilibrium will be attained-
`A(s)+B(g)hArrAB(g)`
`B(g)+C(g)hArrBC(g)`
On adding He gas (inert) to the above system at constant pressure & temperature
View Solution
Exercise-1 (Part-2) questions and complete solutions for chapter CHEMICAL EQUILIBRIUM of RESONANCE ENGLISH of Class 11
All Exercises from RESONANCE Class 11 CHEMISTRY CHEMICAL EQUILIBRIUM
- (MSPs)
- Advanced Level Problems (Part-1)
- Advanced Level Problems (Part-2)(Section-1)
- Advanced Level Problems (Part-2)(Section-2)
- Advanced Level Problems (Part-2)(Section-3)
- Advanced Level Problems (Part-3)(Stage-1)
- Advanced Level Problems (Part-3)(Stage-2)
- Advanced Level Problems (Part-3)(Stage-5)
- Board Level Exercise
- Exercise-1 (Part-1)
- Exercise-1 (Part-2)
- Exercise-2 (Part-1)
- Exercise-2 (Part-2)
- Exercise-2 (Part-3)
- Exercise-2 (Part-4)
- Exercise-3 (Part-1)
- Exercise-3 (Part-2)
- INORGANIC CHEMISTRY(Metallurgy)
- ORGANIC CHEMISTRY(Alkyl Halide, Alcohol,Phenol,Ether)
- PHYSICAL CHMISTRY (CHMICAL EQUILIBRIUM)
- Solved examples