Complete Solutions to Advanced Level Problems of chapter SURFACE TENSION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SURFACE TENSION |
| RESONANCE | Advanced Level Problems |
| Number Of Questions | 17 |
| Academic Year | 2023-24 |
A long capillary tube of radius `r = 1 mm` open at both ends is filled with water and placed vertically. What will be the height (in `cm`) of the column of water left in the capillary walls is negligible. (surface tension of water is `72 "dyne"//"cm"` and `g = 1000 "cm"//"sec"^(2)`)
View SolutionA capillary tube is lowered into a vessel with a liquid whose vapour pressure may be neglected. The density of the liquid is `rho`. The vessel and the tubes are in a vacuum under the bell of air pump (fig). Find the pressure inside the liquid in the capilary tube at a height `h` above the level of the liquid in the vessel
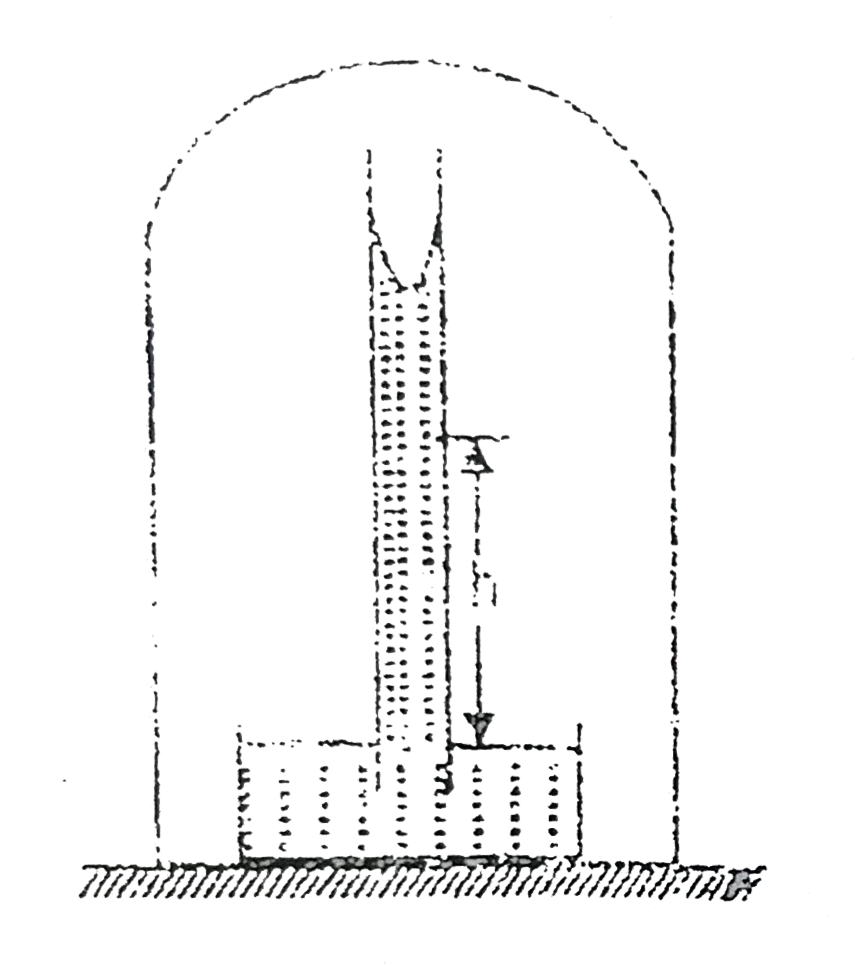
View SolutionIn a device designed by Academician Rebinder the surface tension is determnined from the pressure difference required to form a bubble of air at the end of a capillary immersed in the liquid being investigated (fig). Calculated the surface tension if the radius of the capillary is `r = 1 mm` and the difference in the pressures during bubble formation is `DeltaP = 14 mm` of water column. The end of the capillary is near the surface of the liquid.
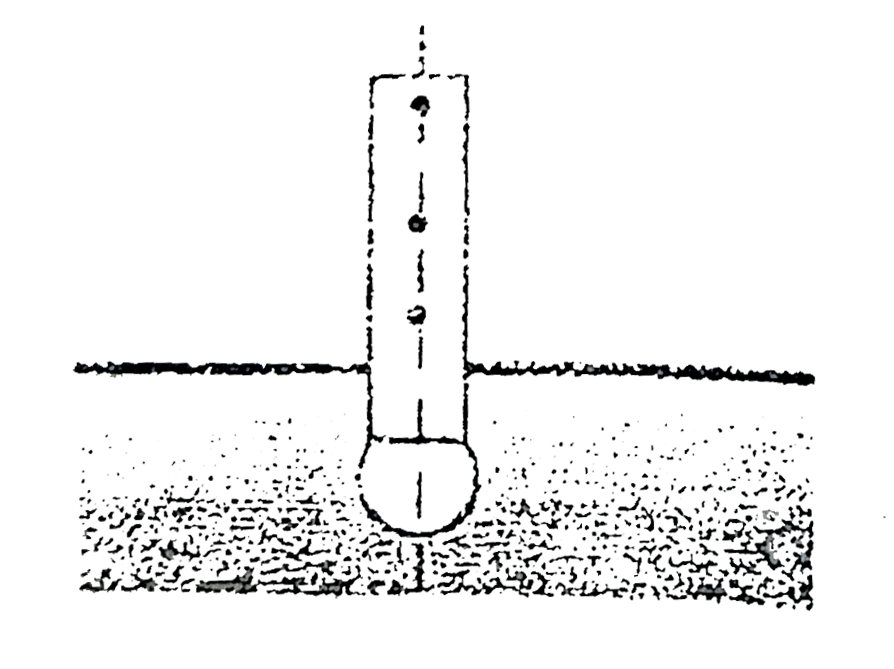
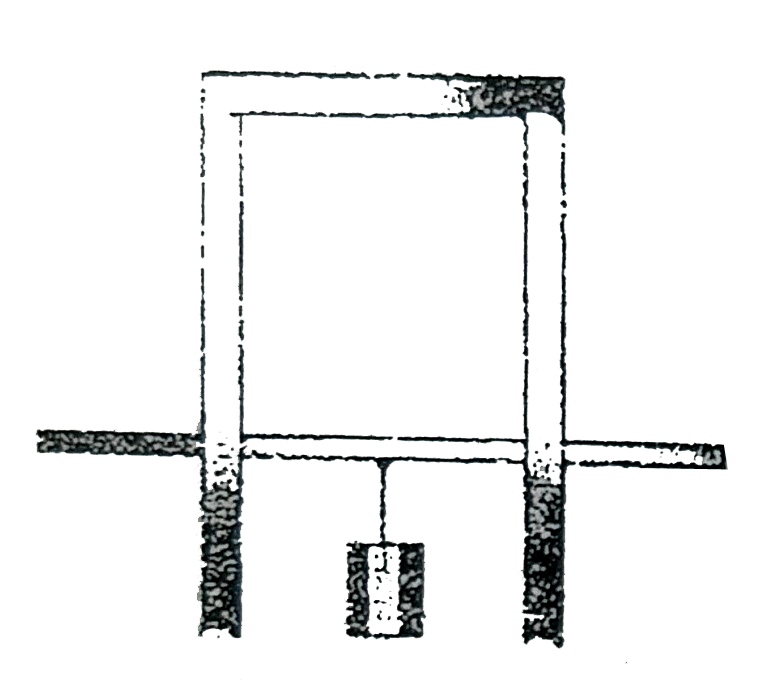
View SolutionA rectagular wire frame with one movable side is convered by a soap film (fig.). What force should be applied to the movable side to counterbalance it ? What work will be done if this side of the frame is moved a distance `S = 2 cm` ? The length of the movable side is `l = 6cm`. The surface tension of the soap film is `alpha = 40 "dyne"//cm`.
View SolutionA capillary of radius `r` is lowered into a wetting agent with surface tension `alpha` and density `d`. Determine the height `h_(0)` to which the liquid will rise in the capillary. Calculate the work done by surface tension and the potential enerfy acquired by the liquid in the capillary and compare the two. Explain the difference in the results obtained.
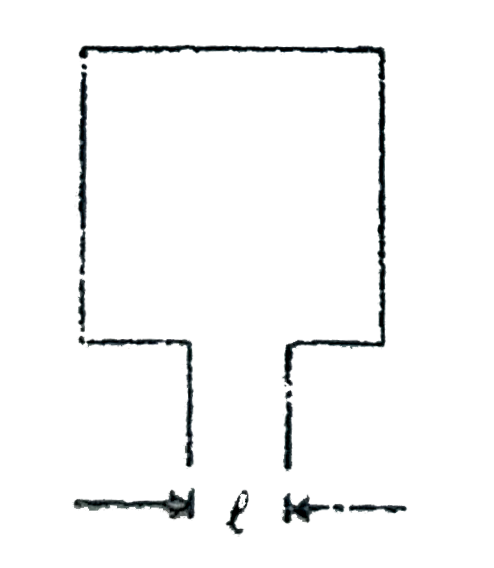
View SolutionA light open rigid paper frame as shown in (Fig.) floats on the surface of water. What will happen to the frame if some soap solution is dropped inside it ? What force will acts on the frame and in what direction will it act ?
View SolutionA `U-`tube is made up of capillaries of bores `1 mm` and `2 mm` respectively. The tube is held vertically and partically filled with a liquid of surface tension `49 "dyne"//"cm"` and zero contact angle. Calculate the density of the liquid of the difference in the levels of the meniscus is `1.25 cm`.
View SolutionA cylinder with a movable piston contains air under a pressure `p_(1)` and a soap bubble of radius 'r' . The pressure `p_(2)` to which the air should be compressed by slowly pushing the piston into the cylinder for the soap bubble to reduce its size by half will be (The surface tension is `sigma` and the temperature T is maintained constant).
View SolutionAssuming the surface tension of rain water to be `72 "dyne"//"cm"`, find the differnce of pressure inside and outside a rain drop of diameter `0.02 cm`. What would this pressure difference amount to , if the drop were to be decreased by evaporation to a diameter of `0.0002 cm` ?
View SolutionA loop of 6.28 cm long thread is put gently on a soap film in a wire loop. The film is pricked with a needle inside the soap film enclosed by the thread. If the surface tension of soap solution is 0.030 N/m, then the tension in the thread is ` x xx 10 ^(-4) N`. find x
View SolutionWhat is the excess pressure inside a bubble of soap solution of radius 500 mm, given that the surface tension of soap solution at the temperature `(20^(@)C)` is `2.50xx10^(-2)Nm^(-1)`? If an air bubble of the same dimension were formed at depth of 40.0 cm inside a container containing the soap solution (of relative density 1.20), what would be the pressure inside the bubble? (1 atmospheric pressure is `1.01xx10^(5)Pa`).
View SolutionThere is soap bubble of radius `2.4xx10^(-4)m` in air cylinder which is originally at the pressure of `10^(5)N//m^(2)` the air in the cylinder is now compressed isothermally unitl the radius of the bubble is halved. Calculate now the pressure of aire in the cylinder the surface tension of the soap film is `0.08Nm^(-1)`
View SolutionA capillary tube of radius `R` is immersed in water and water rises in it to a height h. Mass of water will rise in the capillary tube will be
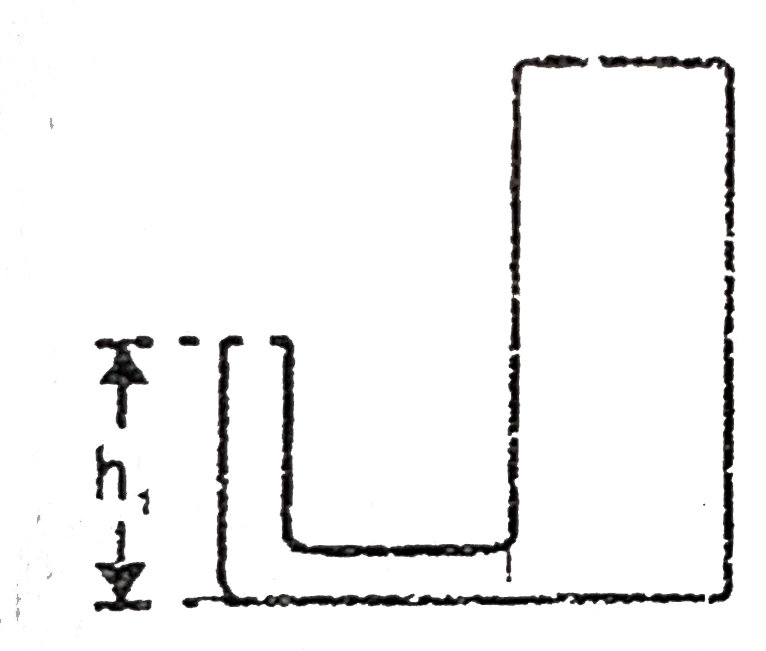
View SolutionA capillary tube of radius `'r'` and height `h_(1)` is connected to a broad tube as shown in fig. The broad tube is gradually filled with drops water falling at equal intervals. Plot the changes in the levels of the water in both tubes with time and changes in the difference between these levels. Calculate the maximum water level in the broad-tube and maximum difference in levels. The surface tension of water is `alpha`.
View SolutionIf the radius and surface tension of a spherical soap bubble are 'R' and 'T' respectively, Then show that the charge required to double its radius would be `8piR ,[epsilon_(0)R[7p_(0)R+12T]]^(1/2)`. Where `p_(0)` is the atmospheric pressure.
View SolutionA closely wound solenoid of 200 turns and area of cross-section `1.5xx10^(-4)m^(2)` carries a current of 2.0 A It is suspended through its centre and perpendicular to its length, allowing it to turn in a horizontal plane in a uniform magnetic field `5xx10^(-2)`T, making an angle of `30^(@)` with the axis of the solenoid. The torque on the solenoid will be
View SolutionThe limbs of a manometer consists of uniform capillary tubes of radii `1.44 xx 10^(-3)m` and `7.2 xx 10^(4 )m`. If the level of the liquid in the narrower tube stands 0.2 m above that in the broader tube, pressure difference between A and B is found to be `310lambda N//m^(2)`. Here `lambda` is an integer. Find `lambda` (density = `10^3 kg//m^3`, surface tension = `72 xx 10^(-3) N//m`). (take `g = 9.8 m//s^2`)
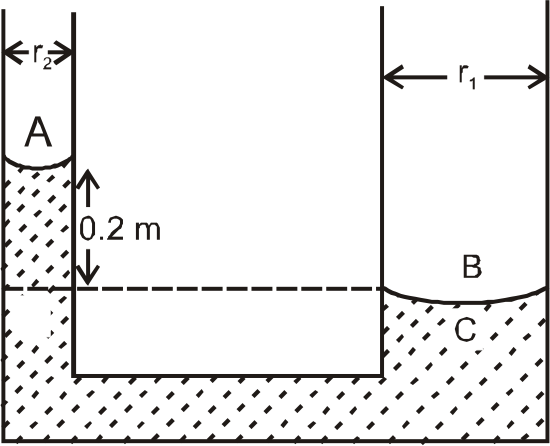
View Solution
Advanced Level Problems questions and complete solutions for chapter SURFACE TENSION of RESONANCE ENGLISH of Class 11