Complete Solutions to Examples of chapter SURFACE TENSION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SURFACE TENSION |
| RESONANCE | Examples |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
Figure shows the container of radius `R` filled with water. Consider an imaginary diametric line drividing the surface in two parts: Left half and right half. Find surface tansion force between the left half surface and the right half surface.

View SolutionConsider the water drop of radius `R`. Find surface tension force between the left half surface and right half surface ?

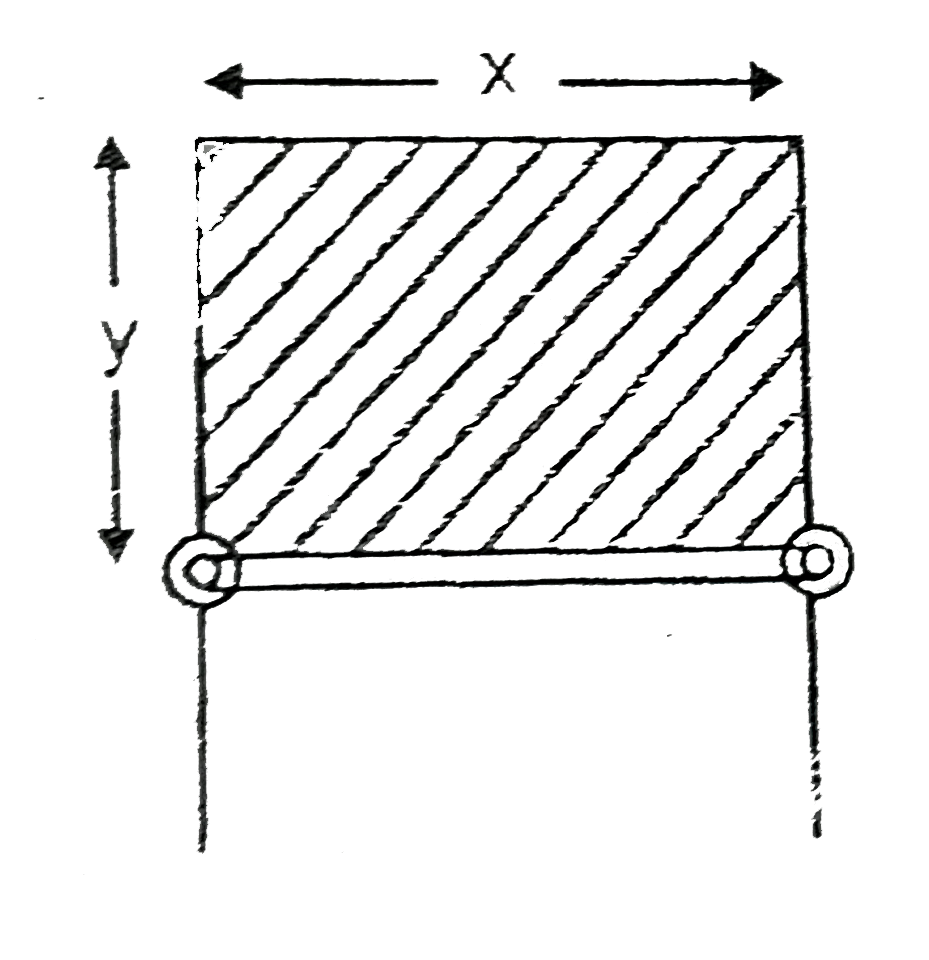
View SolutionBetween a frame and a light slider, a thin film of soap solution is made. Whose length is `x` and width is `y`. Find surface tension force on the slider. To keep the slider in equilibrium, how much weight should be suspended ?
View SolutionIf a liquid drop of water having radius R as shown in figure. The surface tension force between the left half surface and right half surface is (where T is surface tension of liquid`( ##AAK_MCP_15_NEET_PHY_E15_005_Q01##) `
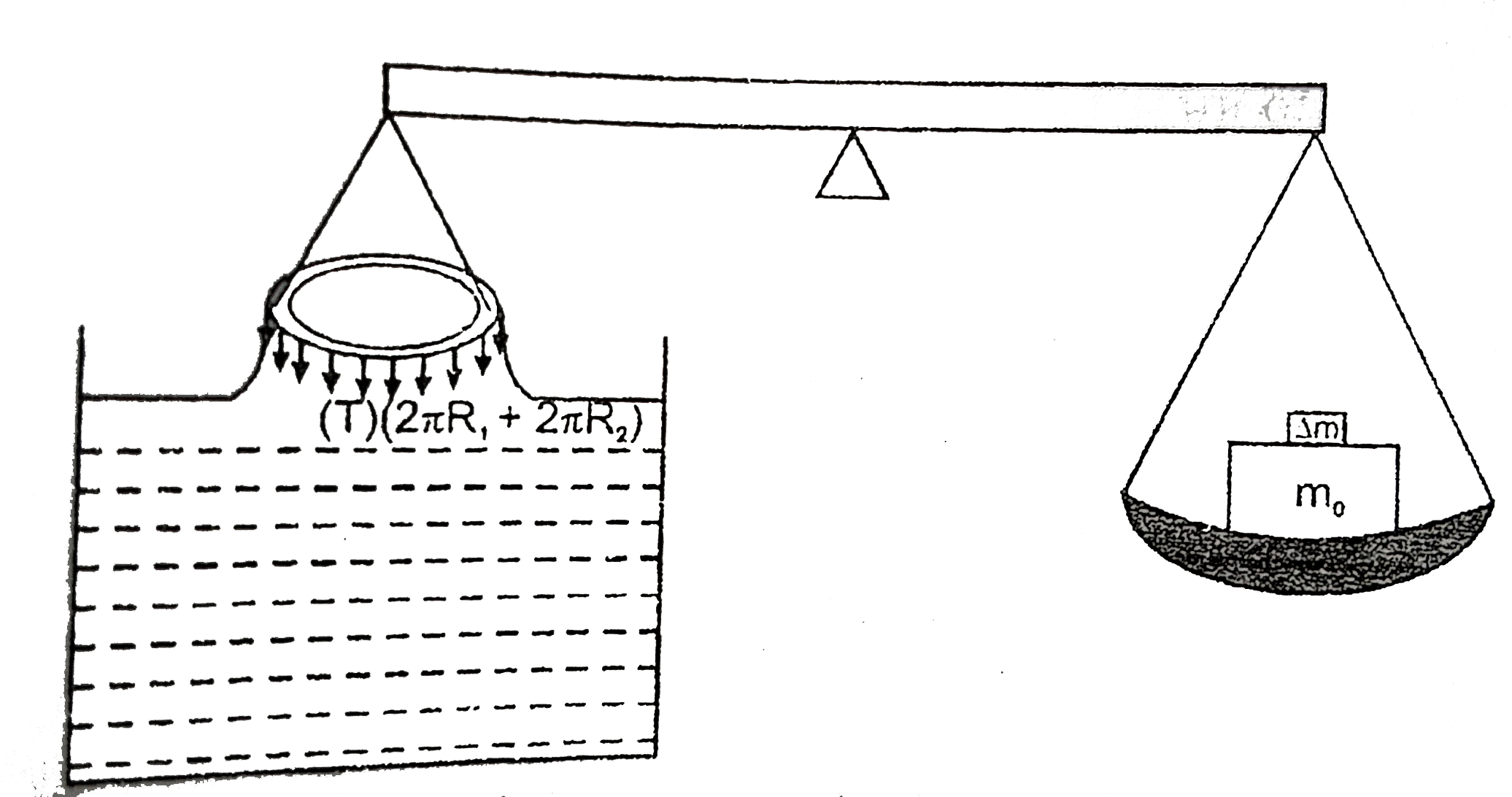
View SolutionA thin disc of radius `R`, just touching the liquid surface forms one arm of a balance. The palte is balanced by some weight on the other side of the balance. How much extra weight should be added on the other side, so that the disc can just come cut of water ?

View SolutionIn the previous question, in place of disc a ring is used whose inner radius is `R_(1)` and outer radius is `R_(2)` Now how much extra weight should be added on the other side, so that the ring can just come out of water ?
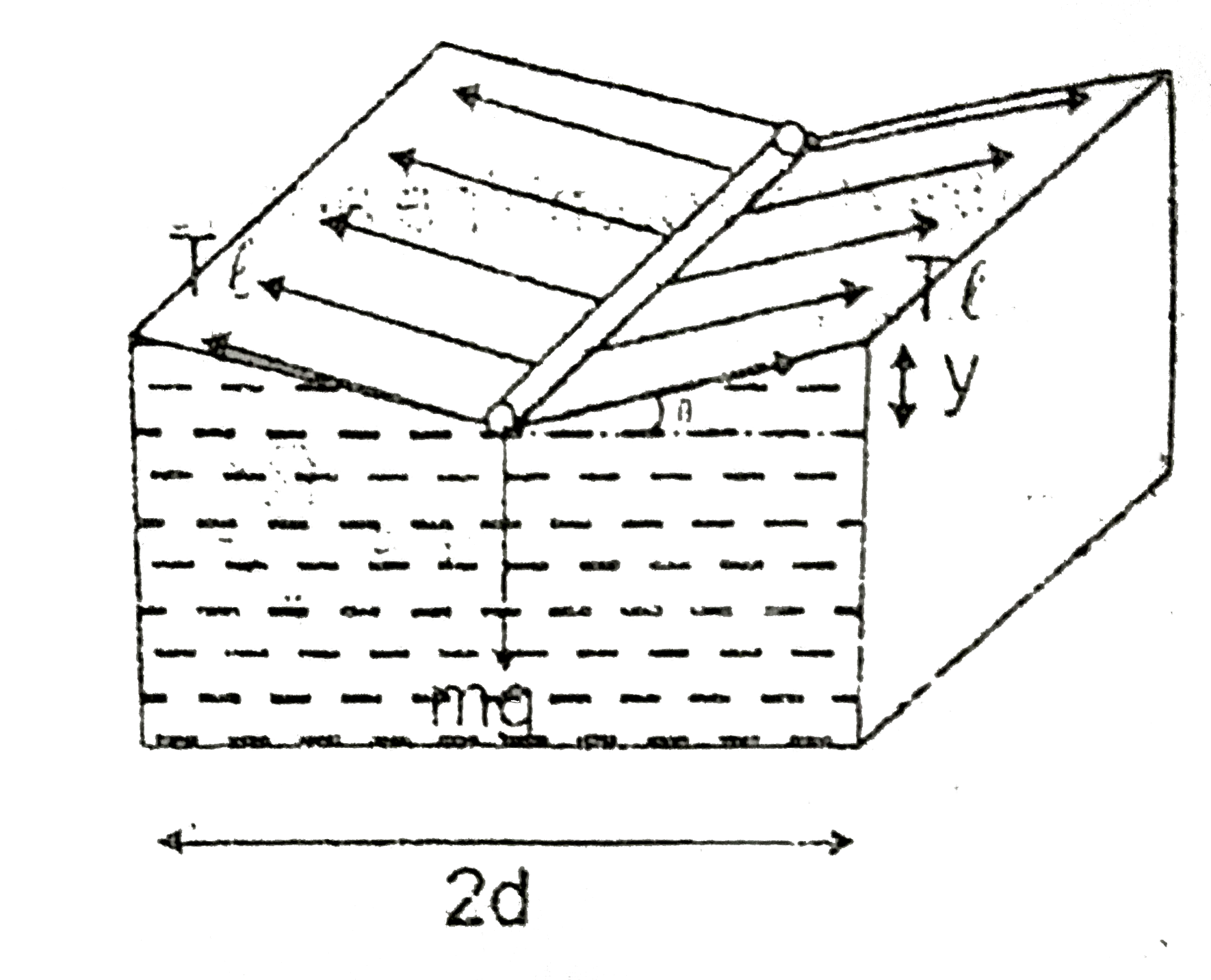
View SolutionA long thin straight uniform wire of negligible radius is supported on the surface of a liquid. The width of the container is `2d` and the wire is kept at its centre, parallel to its length (as shown in figure). The surface of the liquid is depressed by a veritcal distance `y(y lt lt d)` at the centre as shown in figure. If the wire has mass `lambda` per unit length, what is the surface tension of the liquid? igonre end effects.
View Solution`1000` small water drops, each of radius `r`, combine and form a big drop. In this process, find decrease in surface energy.
View SolutionIf a number of little droplets of water, each of radius `r`, coalesce to form a single drop of radius `R`, show that the rise in temperature will be given by `(3T)/J(1/r-1/R)` where `T` is the surface tension of water and `J` is the mechanical equivalent of heat.
View Solution
Water is filled in a capillary tube of radius `R`. If the surface of water is hemispherical `(theta = 0)`, then find pressure at a point `'A'` which is at `h` depth below the surface.
View Solution
Water is filled in a capillary tube of radius R. If the surface of water is hemispherical `(theta = 0)`, then find pressure at a point 'A' which is at h depth below the surface.
View SolutionA small air bubble (cavity of air) of radius `'h'`. Find the pressure inside the bubble.

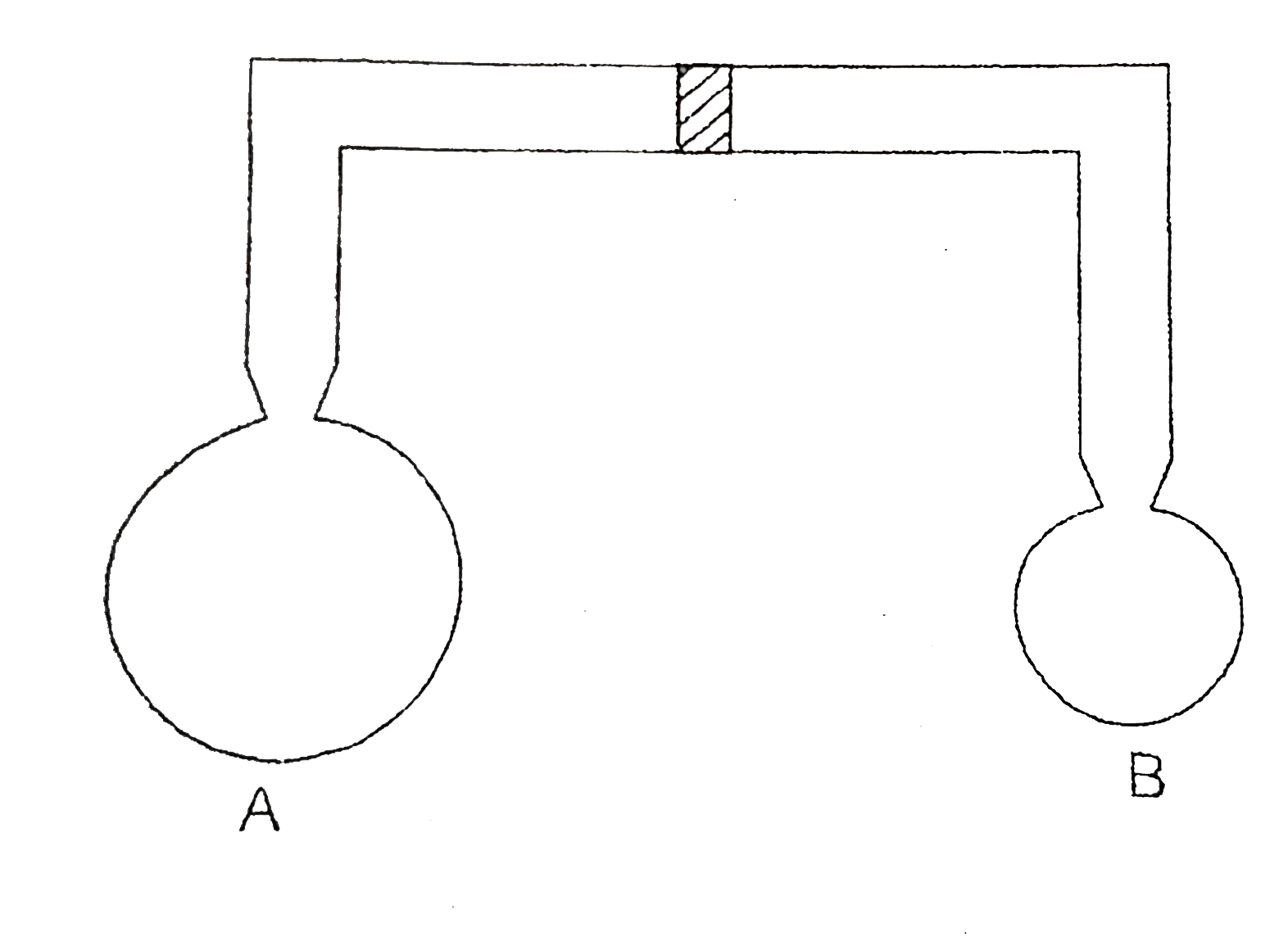
View SolutionTwo soap bubbles are formed on the end of the ends of the tubes as shown. If valve is opened, in which direction will the air flow ?
View SolutionTwo soap bubbles of radius `r_(1)` and `r_(2)` combine. Find radius of curvature of the common surface separating them.

View SolutionA soap bubble of radius `r` and surface tension constant `T` is given a charge, so that its surface charge density is `sigma`. Due to charge, the radius os the soap bubble becomes double then find `'sigma'`. (atmospheric pressure `= P_(0)`)
View SolutionA minute spherical air bubble is rising slowly through a column of mercury contained in a deep jar. If the radius of the bubble at a depth of `100 cm` is` 0.1mm`,Calculate its depth where its radius is `0.126mm`, given that the surface tension of mercury is `567 dyne//cm`. Assume that the atmosphere pressure is `76cm` of mercury.
View SolutionA capillary of internal radius `4 mm`, is dipped in water. To how much height, will the water rise in the capillary. (`T_(water) = 70 xx 10^(-3) N//m, g = 10 m//sec^(2), rho_(water) 10^(3) kg//m^(3)`, contact angle `theta rarr 0`)
View SolutionIf all the glass capillaries have same internal radius, then in which of the capillary, water will ride to move height ?

View Solution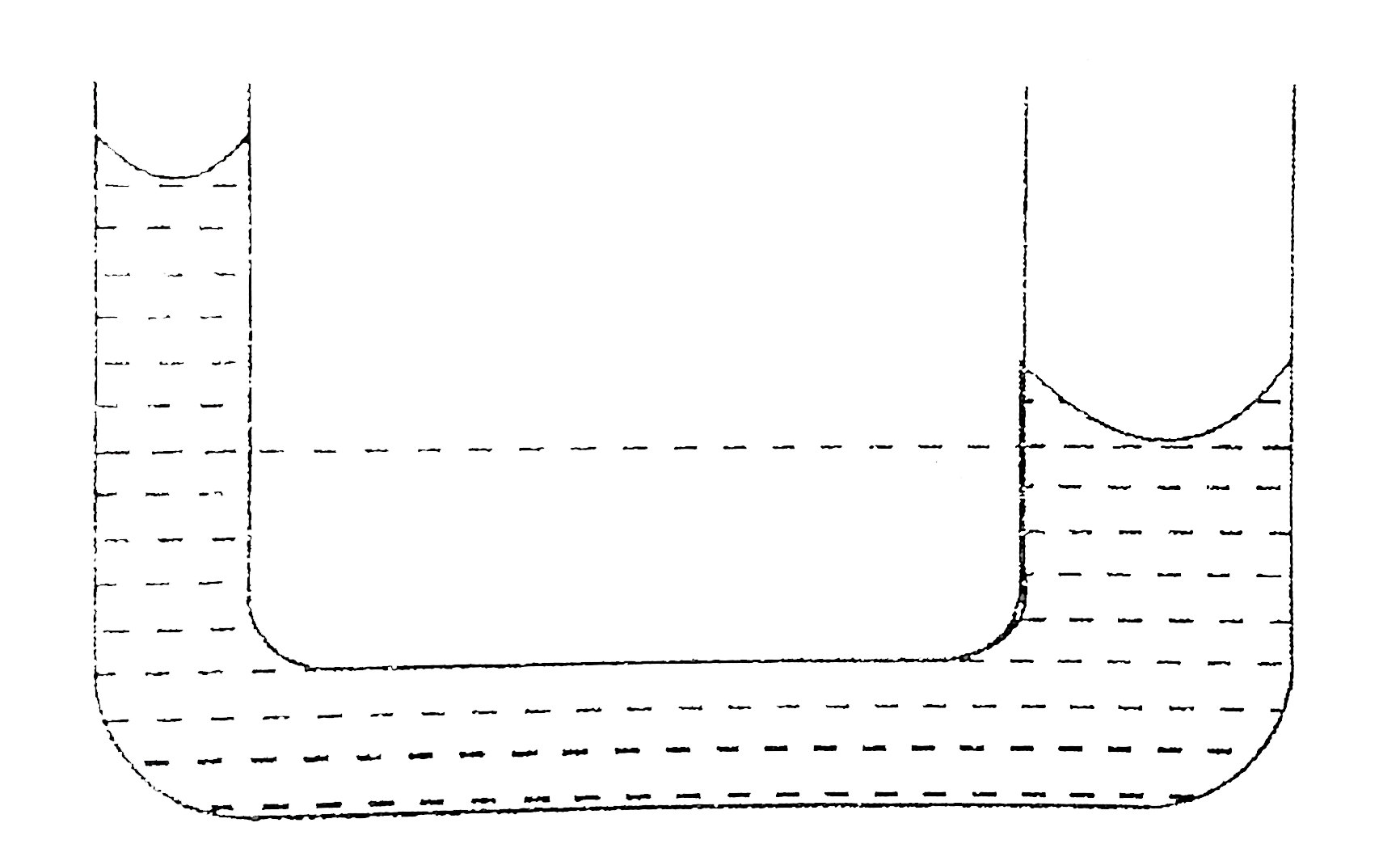
In the `U-`tube, radius of one arm is `R` and the other arm is `2R`. Find the difference in water level if contact angle is `theta = 60^(@)` and surface tension of water is `T`.
View SolutionThere is a small hole of diameter `0.1 mm` at the bottom of a large container. To what minimum height we can fill water in it. so that water doesn't come out of hole. `(T_(water) = 75 xx 10^(-3) N//m)rho_(water) = 10^(3) kg//m^(3), g = 10m//sec^(2)`
View SolutionA barometer contains two uniform capillries of radii `1.44 xx 10^(-3)m` and `7.2 xx 10^(-4)m`. If the height of the liquid in the narrow tube is `0.2 m` more than that in the wide tube, calculate the true pressure difference. Density of liquid `= 10^(3) kg//m^(3)`, surface tension `= 72 xx 10^(-3) N//m` and `g = m//s^(2)`.
View SolutionA liquid of specific gravity `1.5` is observed to rise `3.0cm` in a capollary tube of diameter 0.50mm and the liquid wets the surface of the tube. Calculate the excess pressure inside a spherical bubble of `1.0cm` diameter blown from the same liquid. Angle of contact`=0^(@)`
View SolutionA glass U-tube is such that the diameter of one limb is `3.0mm` and that of the other is 6.0mm. The tube is inverted vertically with the open ends below the surface of water in a beaker. What is the difference between the height to which water rises in the two limbs? Surface tension of water is `0.07Nm^(-1)`. Assume that the angle of contact between water and glass is `0^(@)`.
View SolutionTwo parallel plates which are sparated by a very small distance `d`, are dipped in water. To how much height will the water raise between the plates (Assume contact angle `theta rarr 0`)
View SolutionA thin capillary of inner radius `r_(1)` and outer radius `r_(2)` (The inner tube is solid) is dipped in water. To how much height will the water raise in the tube ? (Assume contact angle `theta rarr 0`)
View SolutionA drop of water of volume `0.05 cm^(3)` is pressed between two glass plates, as a consequence of which, it spreads and occupies an are of `40 cm^(2)`. If the surface tension of water is `70 "dyne"//cm`, find the normal force required to separate out the two glass plates is newton.
View SolutionA glass plate of length `10cm`, breath `1.54 cm`and thickness `0.20cm` weigh `8.2 gm` in air. It is held vertically with the long side horizontal and the lower half under water. Find the apperent weight of the plate. Surface tension of water `=73` dyne per cm, `g=980 cm//sec^(2)`.
View SolutionA glass tube is closed at one end. This end is weighted and the tube floats vertically in water, heavy end down. How far below the water surface is the end of the tube? Given: outer radius of the tube is `0.14 cm`, mass of weighted tube is `0.2 g`, surface tension of water `73 dyn//cm` and `g = 980 cms^(-12)`.
View Solution
Examples questions and complete solutions for chapter SURFACE TENSION of RESONANCE ENGLISH of Class 11