Complete Solutions to Exercise- 3 PART - I of chapter SOUND WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SOUND WAVES |
| RESONANCE | Exercise- 3 PART - I |
| Number Of Questions | 47 |
| Academic Year | 2023-24 |
An observer standing on a railway crossing receives frequencies 2.2 kHz and 1.8 kHz when the tran approaches and recedes from the observer. Find the velocity of the train (speed of sound in air is 300 m/s).
View SolutionAn open pipe is in resonance in 2nd harmonic with frequency `f_(1)`. Now one end of end of the tube is closed and frequency is increased to `f_(2)` such that the resonance again occurs in nth harmonic. Choose the correct option.
View SolutionTwo plane harmonic sound waves are expressed by the equations.
`y_(1)(x,t)=A cos (0.5 pi x-100 pit), y_(2)(x,t)=A cos(0.46 pix-92pi t)` (All parameters are in MKS) :
At x=0 how many times the amplitude of `y_(1) + y_(2)` is zero in one second :-
View SolutionTwo plane harmonic sound waves are expressed by the equations.
`y_(1)(x,t)=A cos (0.5 pi x-100 pit), y_(2)(x,t)=A cos(0.46 pix-92pi t)` (All parameters are in MKS) :
At x=0 how many times the amplitude of `y_(1) + y_(2)` is zero in one second :-
View SolutionTwo plane harmonic sound waves are expressed by the equations.
`y_(1)(x,t)=A cos (0.5 pi x-100 pit), y_(2)(x,t)=A cos(0.46 pix-92pi t)` (All parameters are in MKS) :
At x=0 how many times the amplitude of `y_(1) + y_(2)` is zero in one second :-
View SolutionTwo trains `A and B` moving with speeds `20m//s` and `30m//s` respectively in the same direction on the same straight track, with `B` ahead of `A`. The engines are at the front ends. The engine of train `A` blows a long whistle.
Assume that the sound of the whistle is composed of components varying in frequency from `f_(1) = 800 Hz` to `f_(2) = 1120 Hz`, as shown in the figure. The spread in the frequency (highest frequency - lowest frequency) is thus `320 Hz`. The speed of sound in still air is `340 m//s`.
The speed of sound of the whistle is
View SolutionTwo trains A and B are moving with speeds 20 m/s and 30 m/s, respectively in the same direction on the same straight track with B ahead of A. The engines are at the front ends. The engine of train A blows a long whistle. Assume that the sound of the whistle is composed of components varying in frequency from `f_(1)=800Hz` to `f_(2)=1120Hz`, as shown in the figure. the spread in the frequency (highest frequency-lowest frequency) is thus 320Hz. the speed of sound in still air is 340 m/s.
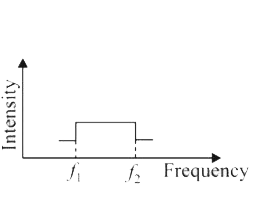
Q. The distribution of the sound intensity of the whistle as observed by the passengers in train A is best represented by :
View SolutionTwo trains `A` and `B` are moving with speeds `20 m//s` respectively in the same direction on the same stright track, with `B` ahead of `A`. The engines are at the front ends. The engines of train `A` blows a long whistle.
Assume that the sound of the whistle is composed of components varying in frequency from `f_(1) = 800 Hz` to `f_(2) = 1120 Hz`, as shown in figure. The speed in the frequency (highest frequency - lowest frequency) is thus `320 Hz`. The speed of sound in still air is `340 m//s`.
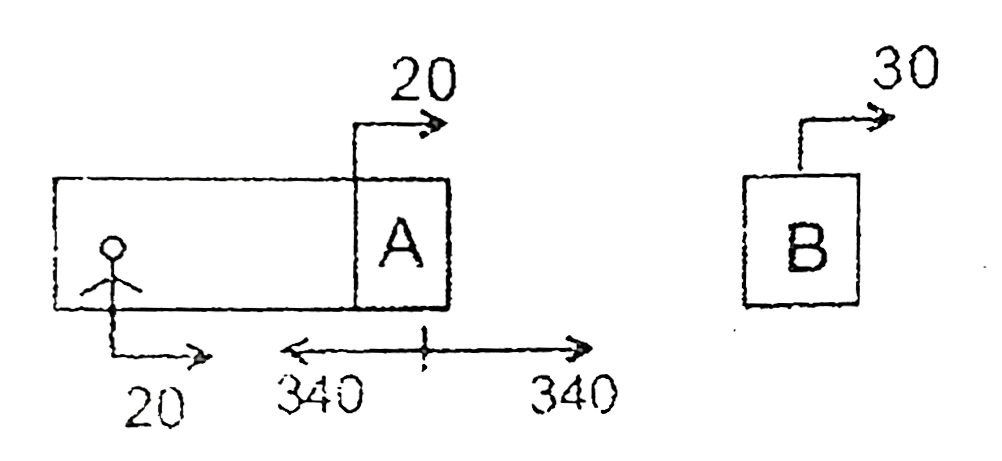
The spread of frequency as observed by the passengers in train `B` is
View SolutionA vibrating string of certain length l under a tension T resonates with a mode corresponding to the first overtone (third harmonic) of an air column of length 75 cm inside a tube closed at one end. The string also generates 4 beats per second when excited along with a tuning fork of frequency n. Now when the tension of the string is slightly increased, the number of beats reduces to 2 per second. Assuming the velocity of sound in air to be 340 m/s, the frequency n of the tuning fork in Hz is
View SolutionA student performed the experiment to measure the speed of sound in air using resonance air-column method. Two resonances in the air-column were obtained by lowering the water level. The resonance with the shorter air-column is the first resonance and that with the longer air-column is the second resonance. Then,
A. the intensity of the sound heard at the first resonance was more than at the second resonance
B. the prongs of the tuning fork were kept in a horizontal plane above the resonance tube
C. the ampitude of vibration of the end of the prongs is typically around `1 cm`
D. the length of the air-column at the first resonance was somewhat than `1//4` th of the wavelength of the sound in air.
View SolutionA stationary source is emitting sound at a fixed frequency `f_(o)`, which is reflected by two cars approaching the source. The difference between the frequencies of sound reflected from the cars is 1.2 % of `f_(o)`. What is the difference in the speeds of the cars (in km per hour) to the nearest integer? Thee cars are moving at constant speeds much smaller than the speed of sound which is 330 `ms^(-1)`
View Solutionhollow pipe of length 0.8 m is closed at one end. At its open end a 0.5 m long uniform strings is vibrating in its second harmonic and it resonates with the fundamental frequency of the pipe. If the tension in the wire is 50 N and the speed of sound is `320ms^(-1)`, the mass of the string is:
View SolutionA police car with a siren of frequency 8 kHz is moving with uniform velocity 36 km/h towards a tall building which reflects the sound waves. The speed of sound in air is 320 m/s. The frequency of the siren heard by the car driver is
View SolutionA person blows into the open-end of a long pipe. As a result, a high-pressure pulse of air travels down the pipe. When this pulse reaches the other end of the pipe
View SolutionA student is performing the experiment of resonance column. The diameter of the column tube is `4 cm`. The frequency of the tuning fork is `512 Hz` The air temperature is `38.^(@) C` in which the speed of sound is `336 m//s`. The zero of the meter scale coincides with the top end of the resonance column tube. When the first resonance occurs, the reading of the water level in the column is.
(a) `14.0 cm`
(b) `15.2 cm`
( c) `6.4 cm` (d) `17.6 cm`.
View SolutionTwo vehicles, each moving with speed u on the same horizontal straight road, are approaching each other. Wind blows along the road with velocity w. One of these vehicles blows a whistle of frequency `f_(1)`. An observer in the other vehicle hears the frequency of the whistle to be `f_(2)`. The speed of sound in still air is V. The correct statement(s) is (are)
View SolutionA student is performing an experiment using a resonance column and a tuning fork of frequency `244s^(-1)`. He is told that the air in the tube has been replaced by another gas (assume that the column remain filled with the gas). If the minimum height at which resonance occurs is `(0.350+-0.005)m`, the gas in the tube is (Useful information: `sqrt(167RT)=640J^(1//2)"mole"^(-1//2):sqrt(140RT)=590J" mole"^(-1//2)`. the molar masses M in grams are given in the options. take the values of `sqrt((10)/(M))` for each gas as given there.)
View SolutionFour harmonic waves of equal frequency and equal intensity `I_(0)` have phase angles `0,(pi)/(3),(2pi)/(3) and pi`. When they are superposed, the intensity of the resulting wave is `nI_(0)`. The value of n is
View SolutionAn observer moves towards a stationary source of sound with a velocity one-fifth of the velocity of sound. What is the percentage increase in the apparent frequency?
View SolutionA whistle producing sound waves of frequencies 9500 Hz and above is approaching a stationary person with velocity v meters per sound. The velocity of sound in air is 300 m/s. If person can hear frequencies up to 10000 Hz, the maximum value of v up to which he can hear the whistle is
View SolutionA sound absorber attenuates the sound level by 20 dB. The intensity decreases by a factor of :
View SolutionThe speed of sound in oxygen `(O_(2))` at a certain temperature is `460 ms^(-1)`. The speed of sound in helium (He) at the same temperature will be (assumed both gases to be ideal)
View SolutionWhile measuring the speed of sound by performing a resonance column experiment, a student gets the first resonance condition at a column length of 18 cm during winter. Repeating the same experiment during summer, she measure the column length to be x cm for the second resonance. Then
View SolutionA motor cycle starts from rest and accelerates along a straight path at `2 m//s^(2)`. At the starting point of the motor cycle there is a stationary electric sire. How far has the motor cycle gone when the driver hears the frequency of the siren at 94% of its value when the motor cycle was at rest ? (speed of sound `= 330 ms^(-1)`)
View SolutionA pipe of length 85 cm is closed from one end.Find the number of possible natural oscillations of air columm in the pipe whose frequencies lie bnelow 1250 Hz.The velocity of sound in air is 340 `m//s`.
View SolutionA train is moving on a straight track with speed `20 ms^(-1)`. It is blowing its whistle at the frequency of 1000 Hz. The percentage change in the frequency heard by a person standing near the track as the train passes him is (speed of sound `= 320 ms^(-1)`) close to :
View SolutionA whistle emitting a sound of frequency `440 Hz` is tied to a string of `1.5 m` length and roated with an angular velocity of `20 rad//s` in the horizontal plane. Calculate the range of frequencies heard by an observer stationed at a larger distance from the whistle .(Speed of sound =`330 m//s)` .
View SolutionWhen `1 m` long metallic wire is stressed, an extension of `0.02 m` is produced. An organ pipe `0.5 m` long and open at both ends, when sounded with this stressed metallic wire, produced `8` beats in its fundamental mode. By decreasing the stress in the wire, the number of beats are found to decrease. Find the Young's modulus of the wire. The density of metallic wire is `10^(4) kg//m^(3)` and velocity of sound in air is `292 m//s`.
View SolutionAt certain instant the shape of a simple train of ple wave is `y = 12sin "(pix)/(50)` (`x` and `y` are in `cm`.). The velocity of the wave propagation is `100 cm//s` in a positive direction away from the origin. Find the equation giving the shape of the wave `0.25s` later.
View SolutionA source of sound of frequency 256 Hz moves rapidly towards a wall with a velocity of `5 ms^(-1).` How many beats per second will be heard if sound travels at a speed of 330 m/s?
View SolutionA particle executes simple harmonic motion with an amplitude of 10 cm and time period 6s. At t=0 it is at position x=5 cm going towards positive x-direction. Write the equation for the displacement x at time t. Find the magnitude of the acceleration of the particle at t=4s.
View SolutionConsider the superposition of `N` harmonic waves of equal amplitude and frequency. If `N` is a very large number determine the resultant intensity in terms of the intensity `(I_(0))` of each component wave for the conditions when the component wave have identical phases.
View SolutionA radio station broadcasting at a frequency of `1500 kHz` gerertes a directional beam by using an array of `4` point ource antennas driver in phase with each other by the same transmitter. The antennas are arranged along an east west line so that each antenna is `50m` from the next one.
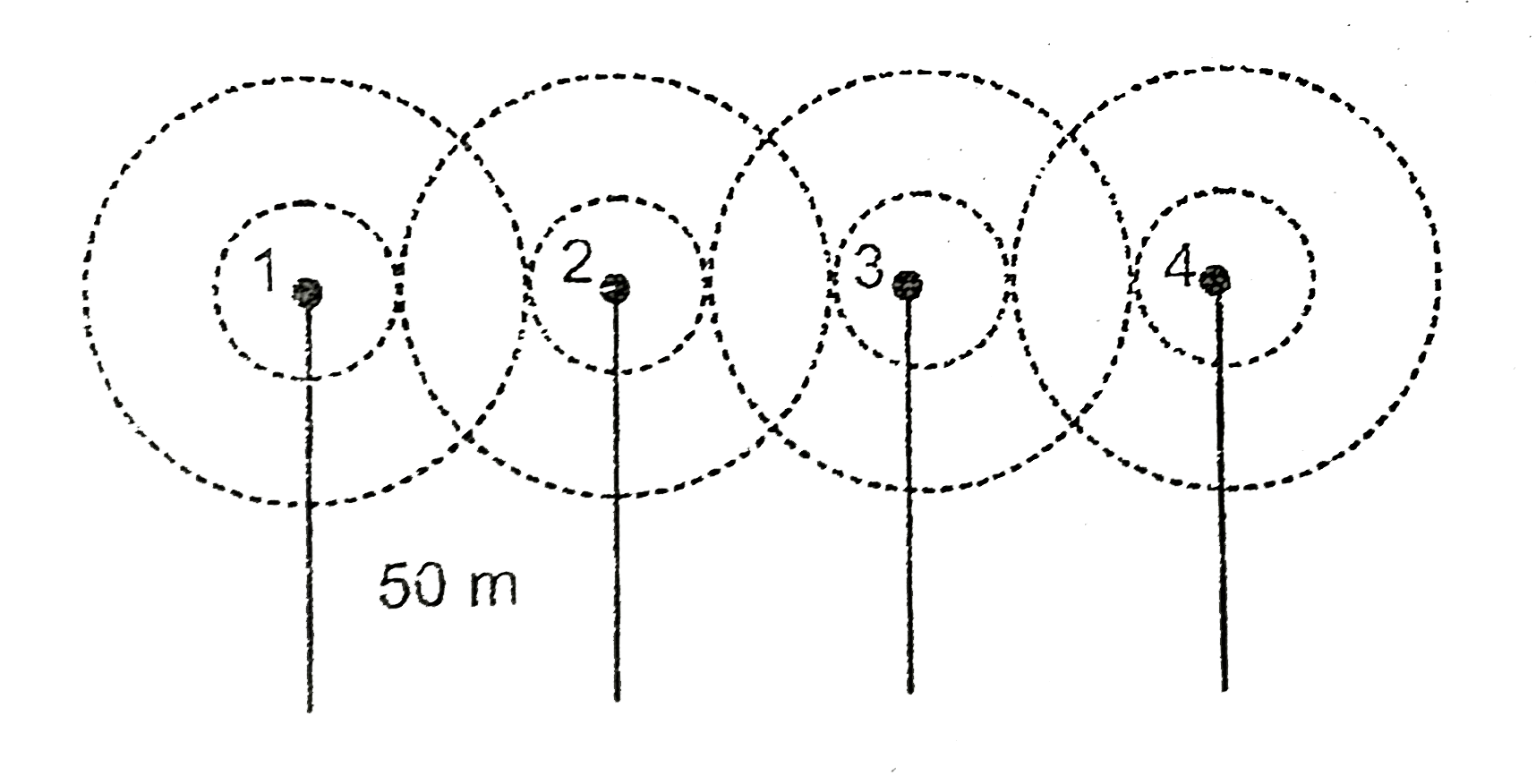
(a) In what direction will be radiated signal to greatest ?
(b) How mcuh signal radiates in east west direction.
View SolutionTwo organ pipes are identical except that one is filled with oxygen and other with a mixture of oxgen and nitrogen. The temperature and total pressure in each pipe are the same when two are sounded together a note of `440 Hz` is heard, which beats one every second. What is the percentage partial pressure of the nitrogen in the mixture ? Assume that the molecular weight of oxygen is `32` and of nitrogen `28`, and their principal specific heats are identical.
View SolutionA military band was marching on a street in the same direction as the normal traffic flow. A motorist was approching the band from behind in his car just at the moment when they were playing the musical note `A` (frequency `440 Hz`) in unison. The same band' performance was also simultaneously being broad live on the ratio from a stationary microphone which was situated on the sidewalk just ahead of the band. The motorist noticed that the combination of the direct sound coming from the band ahead of the band brodcast produced discernible beats. Timing the beats, he counted `4` beats in `3`seconds. He noted from the speedmeter that his car was travelling at `18` kilometers per hour.
Calculate the speed in meters per seconds at which the band was marching assuming that the speed of sound on that day was `330 ms^(-1)`. (It was a very cold day)
View SolutionA person hums in a well and finds strong resonance at frequencies `60 Hz, 100Hz` and `140 Hz`. What is the fundamental frequency of the well? Explain? How deep is the wall ? (velocity of sound `= 344 m//`).
View SolutionA tube `1.0 m` long is closed at one end. A stretched wire is placed near the open end. The wire is `0.3 m` long and a mass of `0.01 kg` . It is held fixed at both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration at its fundamental frequency by resonance. Find
(a) the frequency of oscillation of the air column and
(b) the tension in the wire.
Speed of sound in air = `330 m//s` .
View SolutionThe first overtone of an open orgen pipe beats with the first ouertone of a closed orgen pipe with a beat frequency of `2.2 H_(Z)` . The fundamental frequency of the closed organ pipe is `110 H_(Z)` . Find the lengths of the pipes . Speed of sound in air `u = 330 m//s` .
View SolutionA band playing music at a frequency v is moving towards a wall at a speed `v_(b)`. A motorist is following the band with a speed `v_(m)`.If v is the speed of sound, the expression for the beat frequency heard by the motorist is
View SolutionA `3 m` long organ pipe open at both ends is driven to third harmonic standing wave. If the amplitude of pressure oscillations is `1` per cent of mean atmospheric pressure `(p_(o) = 10^(5) Nm^(2))`. Find the amplitude of particle displacement and density oscillations. Speed of sound `upsilon = 332 m//s` and density of air `rho = 1.03 kg//m^(3)`.
View SolutionThe air column in a pipe closed at one end is made to vibrated in its second overtone by a tuning fork of frequency `440 H_(Z)` . The speed of sound in air is `330 m//s` . End corrections may be neglected. Let `p_(o)` denotes the mean pressure at any point in the pipe, end `Delta p_(o)` the maximum amplitude of pressure variation.
(a) Find the length `L` of the air column.
(b) What is the amplitude of varitation at the middle of the column ?
(c) What are the maximum and minimum pressures at the open end of the pipe?
(d) What are the maximum and minimum pressure at the closed end of the pipe ?
View SolutionA source of sonic oscillations with frequency `n=1700Hz` and a receiver are located on the same normal to a wall. Both the source and receiver are stationary, and the wall recedes from the source with velocity `u=6.0(m)/(s)`. Find the beat frequency registered by the receiver. The velocity of sound is `v=340(m)/(s)`.
View SolutionA man standing in front of a mountain beats a drum at regular intervals. The drumming rate is gradually increased and he finds that echo is not heard distinctly when the rate becomes `40` per minute. He then moves near to the mountain by `90` metres and finds that echo is again not heard distinctly when the drumming rate becomes `60` per minute. Calculate (a) the distance between the mountain and the initial position of the man and (b) the velocity of sound.
View SolutionA source is moving across a circle given by the equation `x^(2) + y^(2) = R^(2)` with constant speed `v_(S) = (330pi)/(6sqrt(3))m//s`. In clockwise sense. A detector is stationary at the point `(2R, 0) w.r.t.` the centre of the circle. The frequency emitted by the source is `f_(S)`.
(a) What are the co-ordinates of the source when the detector records the maximum and minimum frequencies. Take speed of sound `v = 330 m//s`.
View SolutionA sonar system fixed in a submariene operatres at a frequency 40KHz. An enemey submarine moves towards the sonar with a speed of `360kmh^(-1)`. What is the frequency of sound reflected by the submarine? Speed of sound in water `1450ms^(-1)?`
View SolutionA road passes at some distance from a standing man. A truck is coming on the road with some acceleration. The truck driver blows a whistle of frequency `500 Hz` when the line joining the truck and the man makes an angle `theta` with the road. The man hears a note having a note having a frequency of `600 Hz` when the truck is closest to him. Also the speed of truck has get doubled during this time. Find the value of `'theta'`.
View SolutionAt `t = 0`, a source of sonic oscillations `S` and on observer `O` start moving along `x` and `y` axes with `5 m//s` and `10 m//s`. The figure shows their positions at `t = 0`. If frequency of source is `1000 Hz`. Find the frequency of singals received after `5` second. `V_(sound) = 330 m//sec`.

View Solution
Exercise- 3 PART - I questions and complete solutions for chapter SOUND WAVES of RESONANCE ENGLISH of Class 11