Complete Solutions to Exercise- 1 PART - I of chapter SOUND WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SOUND WAVES |
| RESONANCE | Exercise- 1 PART - I |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
The audible frequency for a normal human being is `20 Hz` to `20 kHz`. Fuind the corresponding wavelengths if the speed of sound in air `320 m//s`.
(b) Find the phase difference between two position separated by `20 cm` at a particular instant.
View SolutionA sound wave of frequency `80 Hz` is travelling with speed `320 m//s`.
(a) Find the change in phase at a given position in `400 ms`
(b) Find the phase difference between two positions seperated by `20 cm` at a particular instant.
View SolutionA travelling sound wave is described by the equation `y = 2sin(4t - 5x)` where `y` is measured in centimeter. `t` in seconds and `x` in meters.
(a) Find the ratio of amplitude and wavelength of wave.
(b) Find the ratio of maximum velocity of particular to wave velocity.
View SolutionThe pressure at a point varies from `99980 Pa` to `100020 Pa` due to simple harmonic sound wave. The amplitude and wavelength of the wave are `5 xx 10^(-6) m` and `40 cm` respectively. Find the bulk modulus of air
View SolutionFind the minimum and maximum wavelengths of sound in water that is in the audible range for an average human ear. Speed of sound in water is `1450 m//s`.
View SolutionA man standing between two parallel hills, claps his hand and hears successive echoes at regular intervals of 1s. If velocity of sound is 340 m `s^(-1)`, then the distance between the hills is
View SolutionFind the speed of sound in a mixture of 1 mole of helium and 2 moles of oxygen at `27^(@)C`. If the temperature is raised by 1K from 300K, find the percentage change in the speed of sound in the gaseous mixture.
Take `R=8.31Jmo l e^(-1)K^(-1)`.
View SolutionA gas mixture has `24%` of Argon, `32%` of oxygen, and `44%` of `CO_(2)` by mass. Find the velocity of sound in the gas mixture at `27^(@)C`. Given `R = 8.4 S.I.` units.
Molecular weight of `Ar = 40, O_(2) = 32, CO_(2) = 44, gamma_(Ar) = 5//3 gamma_(O2) = 7//5, gamma_(CO_(2)) = 4//3`.
View SolutionTwo sound waves one in air and the other in fresh water are equal in intensity.
(a) Find the ratio of pressure amplitude of the wave in water to that of the wave in air.
(b) If the pressure amplitudes of the waves are equal then what will be the ratio of the intensities of the waves.
[`V_(sound) = 340 m//s` in air & density of air `= 1.25 kg//m^(3), V_(sound) = 1530 m//s` in water, density of water `= 1000 kg//m^(3)`]
View SolutionA point `A` is located at a distance `r = 1.5 m` from a point source of sound of frequency `600 H_(Z)`. The power of the source is `0.8 W`. Speed of sound in air is `340 m//s` and density of air is `1.29 kg//m^(3)`. Find at the point `A`, (a) the pressure oscillation amplitude`(Deltap)_(m)` (b) the displacement oscillation amplitude `A`.
View SolutionTwo point sound sources `A` and `B` each to power `25pi w` and frequency `850 Hz` are `1 m` apart. The sources are in phase
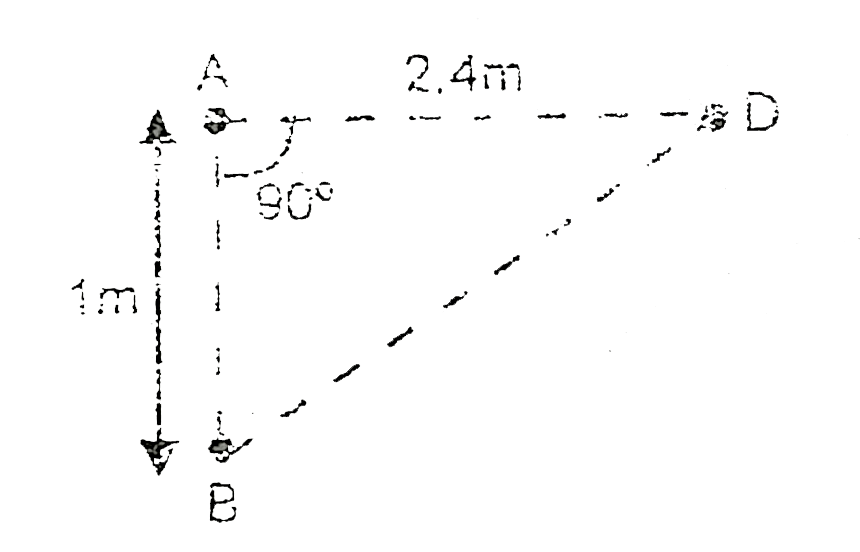
Determine the phase difference between the waves emitting from `A` and `B` received by detector `D` as shown in figure. Velocity of sound `= 340 m//s`.
View SolutionTwo identical loudspeakers are located at point `A` & `B, 2 m` apart. The loudspeakers are driven by the same amplifier (coherent and are in phase). A small detector is moved out from point `B` along a line frequency below which there will be no position
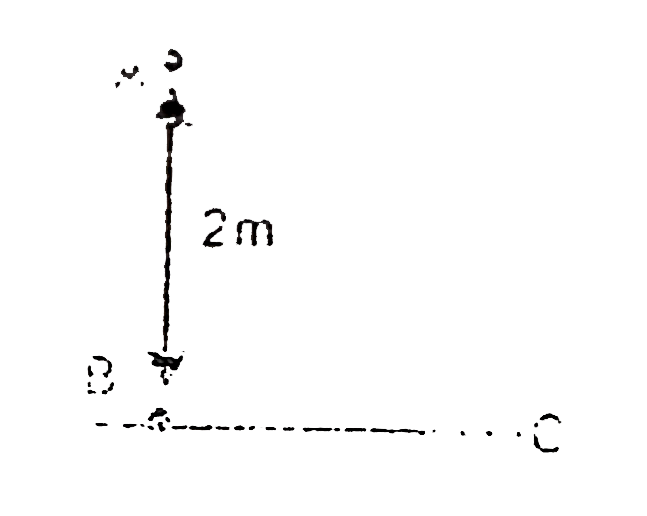
View SolutionA sound sources, detector and a movable wall are arranged as shown in figure. In this arrangement detectir us detacting the maximum intensity. If the speed of sound is `330 m//s` in air and frequency of source is `660 Hz`, then find the minimum distance by which the wall should be moved away from source, so that detector dtects minimmum intensity.

View SolutionTwo source of sound, `S_(1)` and `S_(2)`, emitting waves of equal wavelength `2 cm`, are placed with a separation of `3 cm` between them. A detector can be moved on a line parallel to `S_(1) S_(2)` and at a distance `24 cm` from it. Initially, the detecor is equidistant from the two sources. Assuming that the waves emitted by the sources are in phase, find the minimum distance through which the detector should be shifted to detect a minimum of sound.
View SolutionA sound source, detector and a cardboard are arranged as shown in figure. The wave is reflected from the cardboard at the line symmetry of source edetector. Initially the path difference between the reflected wave and the direct wave is one third of the wavelength of sound. Find the minimum distance by which the cardboard should be moved upwards so that both waves are in phase.
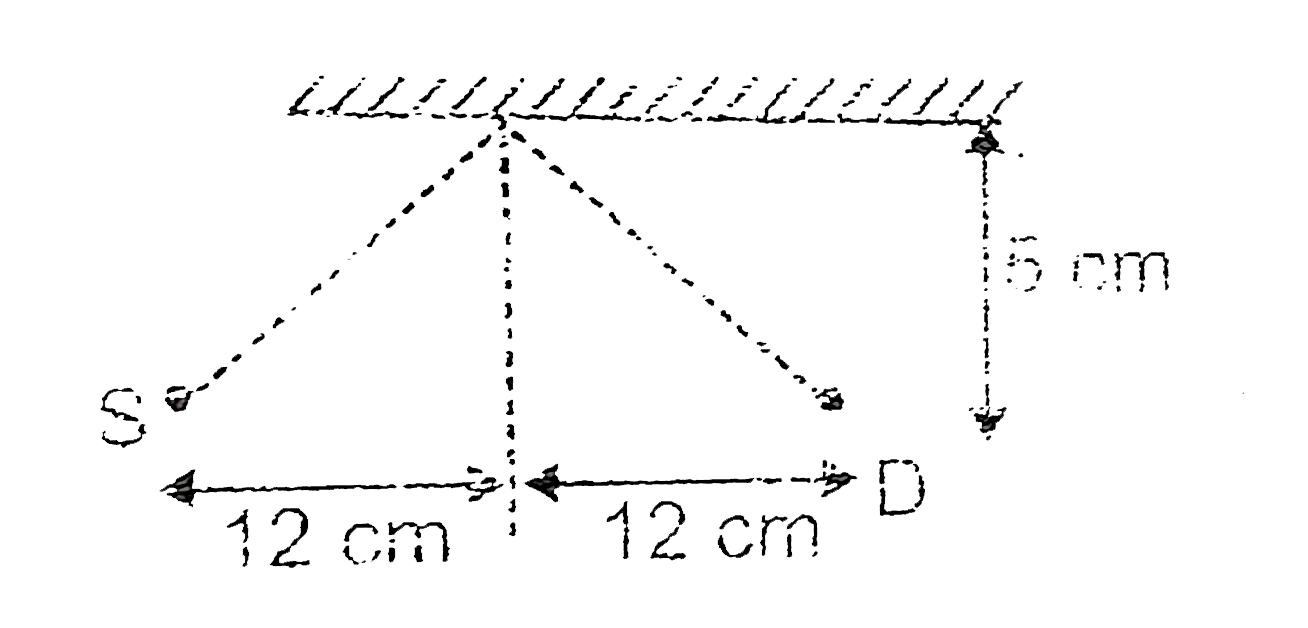
View SolutionA metallic rod of length 1 m is rigidly clamped at its midpoint. Longitudinal stationary waves are set up in the rod in such a way that there are two nodes on either side of the midpoint. The amplitude of an antinode is `2xx10^(-6)m`.
(i) Write the equation of motion at a point 2 cm from the midpoint __________ (ii) Write the equation of constituent waves in the rod _________ `(Y=2xx10^(11)N//m^(2) and rho=8xx10^(3)kg//m^(3))`.
View SolutionThe equation of a longitudinal standing wave due to superposition of the progressive waves producted by two sources of sound is `s = -20 sin 10 pix sin 100 pit` where `s` is the displacement from mean position measured in `mm, x` is in meters and is in seconds. The specific gravity of the medium is `10^(-3)`. Density of water `= 10^(3)kg//m^(3)`. Find :
(a) Wavelength, frequency and velocity of the progressive waves.
(b) Bulk modulus of the medium and the pressure amplitude.
(c) Minimum distance between pressure antinode and a displacement anotinode.
(d) Intensity at the displacement nodes.
View SolutionA closed organ pipe has length `L`. The air in it is vibrating in third overtone with maximum amplitude a . The amplitude at distance`(L)/(7)` from closed of the pipe is a) 0 b) a c) a/2 d) data insufficient
View SolutionThe speed of sound in an air column of `80 cm` closed at one end is `320 m//s`. Find the natural freqencies of air column between `20 Hz` and `2000 Hz`.
View SolutionIn an organ pipe the distance between the adjacent node is `4 cm`. Find the frequency of source if speed of sound in air is `336 m//s`.
View SolutionTwo pipes `P_(1)` and `P_(2)` are closed and open respectively. `P_(1)` has a length of `0.3 m`. Find the length of `P_(2)`, if third harmonic of `P_(1)` is same as first harmonic of `P_(2)`.
View SolutionTwo successive resonance frequencies in an open organ pipe are 1944 Hz and 2592 Hz. Find the length of the tube. The speed of sound in air is `324 m s^-1`.
View SolutionA closed organ pipe of length `l = 100 cm` is cut into two unequal pieces. The fundamental frequency of the new closed organ pipe place is found to be same as the frequency of first overtone of the open organ pipe place. Datermine the length of the two piece and the fundamental tone of the open pipe piece. Take velocity of sound `= 320 m//s`.
View SolutionFind the number of possible natural oscillations of air column in a pipe whose frequencies lie below `f_(0) = 1250 Hz`. The length of the pipe is `l = 85 cm`. The velocity of sound is `v = 340 m//s`. Consider two cases
the pipe is closed from one end .
View SolutionA source of sound with adjustable frequency produces 2 . beats per second with a tuning fork when its frequency is either 476 Hz or 480 Hz. What is the frequency of the tuning fork ?
View SolutionTwo indentical piano wires, kept under the same tension T have a fundamental frequency of 600Hz. The fractional increase in the tension of one of the wires which will lead to occurrence of 6 beats/s when both the wires oscillate together would be :
View SolutionA metal wire of diameter `1 mm` is held on two knife edges by a distance `50 cm`. The tension in the wire is `100 N`. The wire vibrating with its fundamental frequency and a vibrating tuning fork together produce `5 beats//s`. The tension in the wire is then reduced to `81 N`. When the two are excited, beats are heard at the same rate. Calculate
(a) frequency of a fork and
(b) the density of material of wire.
View SolutionA string `25 cm` long and having a mass of `2.5 g` is under tension. A pipe closed at one end is `40 cm` long . When the string is set vibrating in its first overtone and the air in the pipe in its fundamental frequency, `8` beats per second are heard . It is observed that decreasing the tencion in the string decrease the beat frequency. If the speed of sound in air is `320 m//s`, find the tension in the string.
View SolutionAn observer rides with a sound source of frequency `f` and moving with velocity `v` towards a large vertical wall. Considering the velocity of sound waves as `c`, find :
(i) The number of waves striking the surface of wall per second
(ii) The wavelength of the reflected wave
(iii) The frequency of reflected wave as observed by observer.
(iv) Beat frequency heard by the observer.
View SolutionA stationary source sends forth monochromatic sound. A wall approaches it with velocity 33 cm/s. The propagation velocity of sound in the medium is `c=330(m)/(s)`. How much, in per cent , does the wavelength of sound change on reflection from the wall?
View SolutionA source of sonic oscillations with frequency `n_(0)=600Hz` moves away and at right angles to a wall with velocity `u=30ms^(-1)`. A stationary receiver is located on the line of motion of the source in the succession wall`to`source`to`receiver. If velocity of sound propagation is `v=330ms^(-1)`, calculate
View SolutionA sound wave of frequency `f` propagating through air with a velocity `c`, is reflected from a surface which is moving away from the source with a constant speed `v`. Find the frequency of the reflected wave, measured by the observer at the position of the source.
View Solutiontwo trains move towards each other sith the same speed. The speed of sound is 340 m/s. If the height of the tone of the whistle of one of them heard on the other changes 9/8 times, then the speed of each train should be
View SolutionA tuning fork `P` of unknows frequency gives `7` beats in `2` seconds with another tuning fork `Q`. When `Q` runs towards a wall with a speed of `5 m//s` it gives `5` beats per second with its echo. On loading `P` with wax, it gives `5` beats per second with `Q` . What is the frequency of `P`? Assume speed of sound = `332 m//s` .
View Solution
Exercise- 1 PART - I questions and complete solutions for chapter SOUND WAVES of RESONANCE ENGLISH of Class 11