Complete Solutions to Exercise- 2 PART - II of chapter FLUID MECHANICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FLUID MECHANICS |
| RESONANCE | Exercise- 2 PART - II |
| Number Of Questions | 6 |
| Academic Year | 2023-24 |
A closed tube in the form of an equilateral triangle of side `l` contains equal volumes of three liquids which do not mix and is placed vertically with its lowest side horizonta. Find 'x' in the figure if the densities of the liquids are in `A.P`.
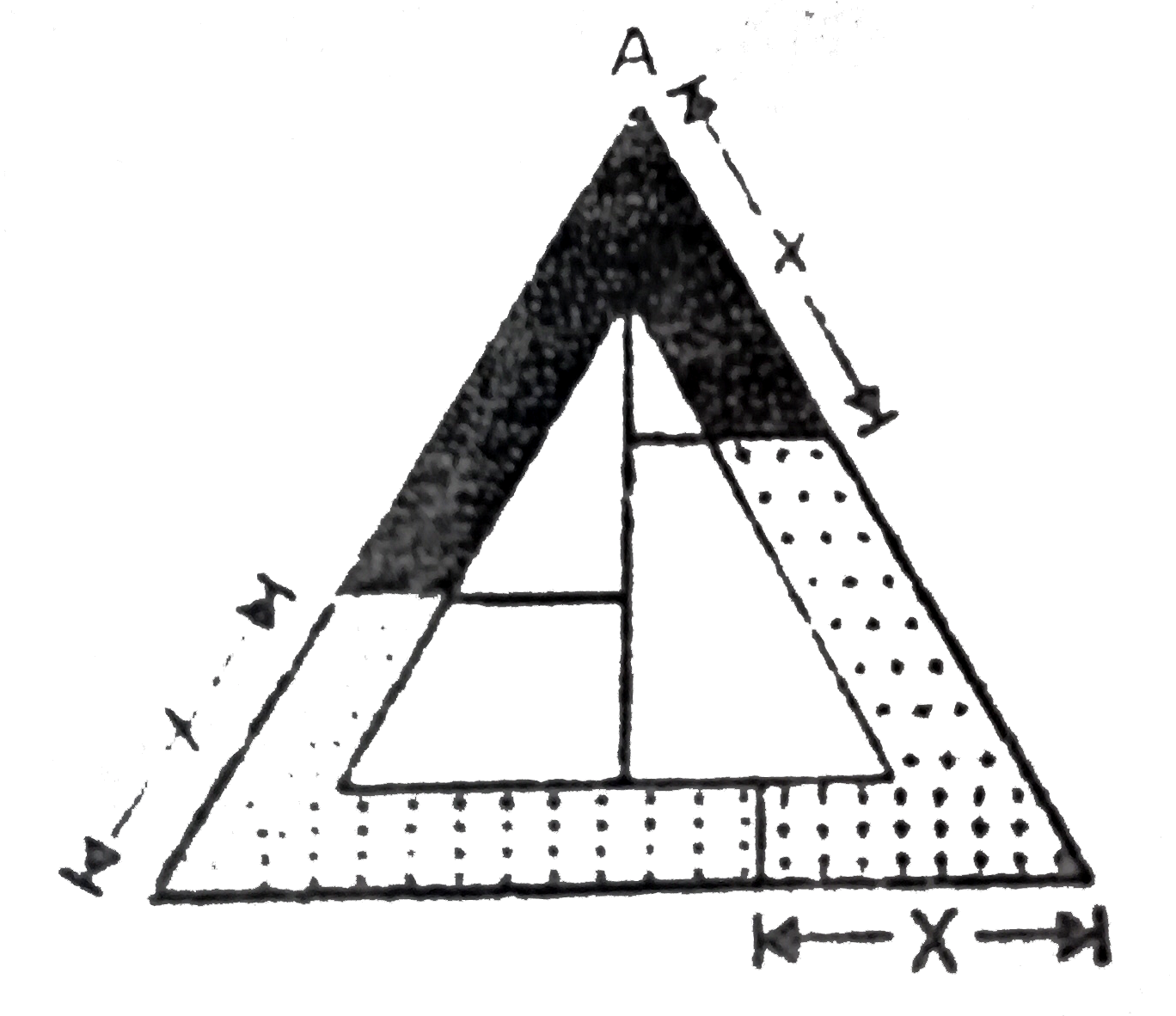
View SolutionAn open tank `10 m` long and `2 m` deep is filled up to `1.5 m` height of oil of specific gravity `0.82`. The tank is uniformly accelerated along its length from rest to a speed of `20 m//s` horizontally. The shortest time in which the speed may be attained without spilling any oil is
View SolutionFigure shows a cubical block of side 10 cm and relative density 1.5 suspended by a wire of cross sectional area `10^(-6) m^(2)`. The breaking stress of the wire is `7 xx 10^(6) N//m^(2)`. The block is placed in a beaker of base area `200 cm^(2)` and initially i.e. at t = 0, the top surface of water & the block coincide. There is a pump at the bottom corner which ejects `2 cm^(3)` of water per sec. Find the time at which the wire will break.
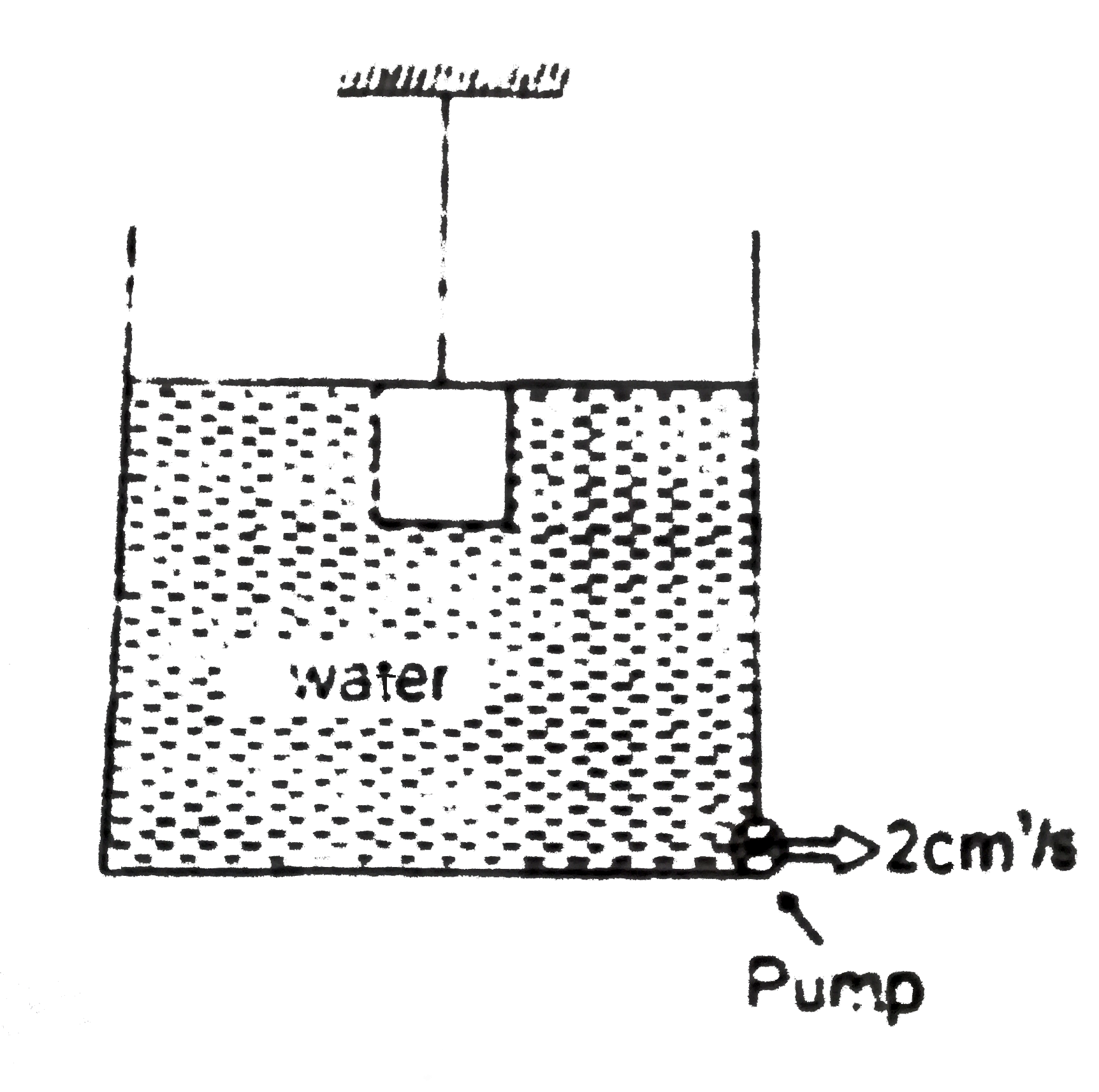
View SolutionA tank containing gasoline is sealed and the gasoline is under pressure `P_(0)` as shown in the figure. The stored gasoline hs a density of `660 kg m^(-3)`. A sniper fires a rifle bullet into the gasoline tank, making a small hole `53 m` below the surface of gasoline. The total height of gasoline is `73 m` from the base. The jet of gasoline shooting out of the hole strikes the ground at a distance of `80 m` from the tank initially. If the pressure above the gasonline surface is `(1.39)alpha xx 10^(5)N//m^(2)` than `alpha` is- (The local atmospheric pressure is `10^(5)Nm^(-2)`)
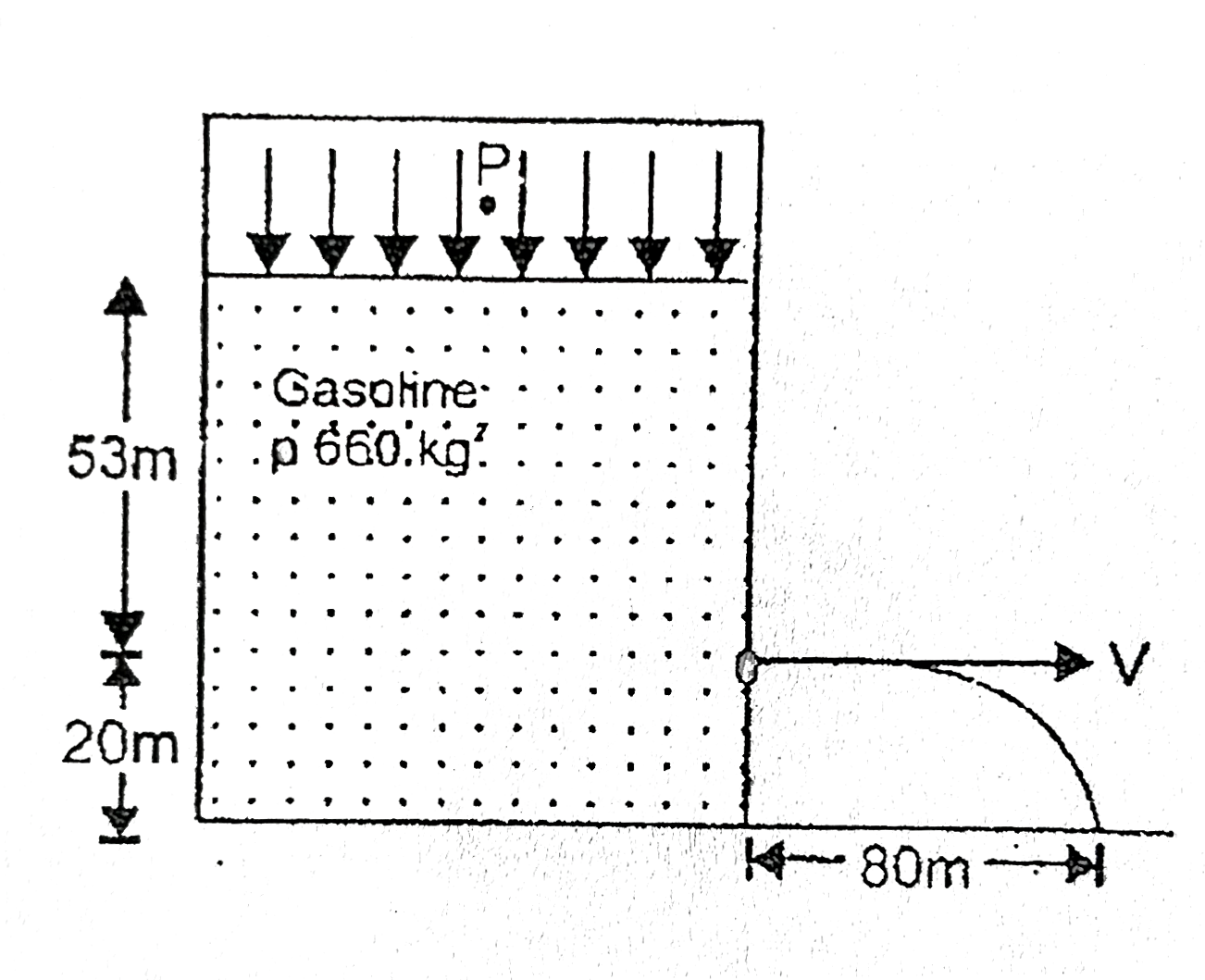
View SolutionA large open top container of negligible mass and uniform cross sectional area `A` a has a small hole of cross sectional area `A//100` in its side wall near the bottom. The container is kept on a smooth horizontal floor and contains a liquid of density `rho` and mass `M_(0)`. Assuming that the liquid starts flowing out horizontally through the hole at `t=0`, calculate a the acceleration of the container and b its velocity when `75%` of the liquid has drained out.
View SolutionA non-viscous liquid of constant density `1000 kg//m^(3)` flows in a streamline notion along a tube of variable cross-section. The tube is kept inclined in the vertical plane as shown in the figure. The area of cross-section of the tube at two points `P` and `Q` at heights of 2m and 5m are respectively `4xx10^(3)m^(2)` and `8xx10^(-3)m^(2)`. The velocity of the liquid at point P is `1m//s`. Find the work done per unit volume by the pressure and the gravity forces as the fluid flows from point P to Q. Take `g=9.8m//s^(2)`.
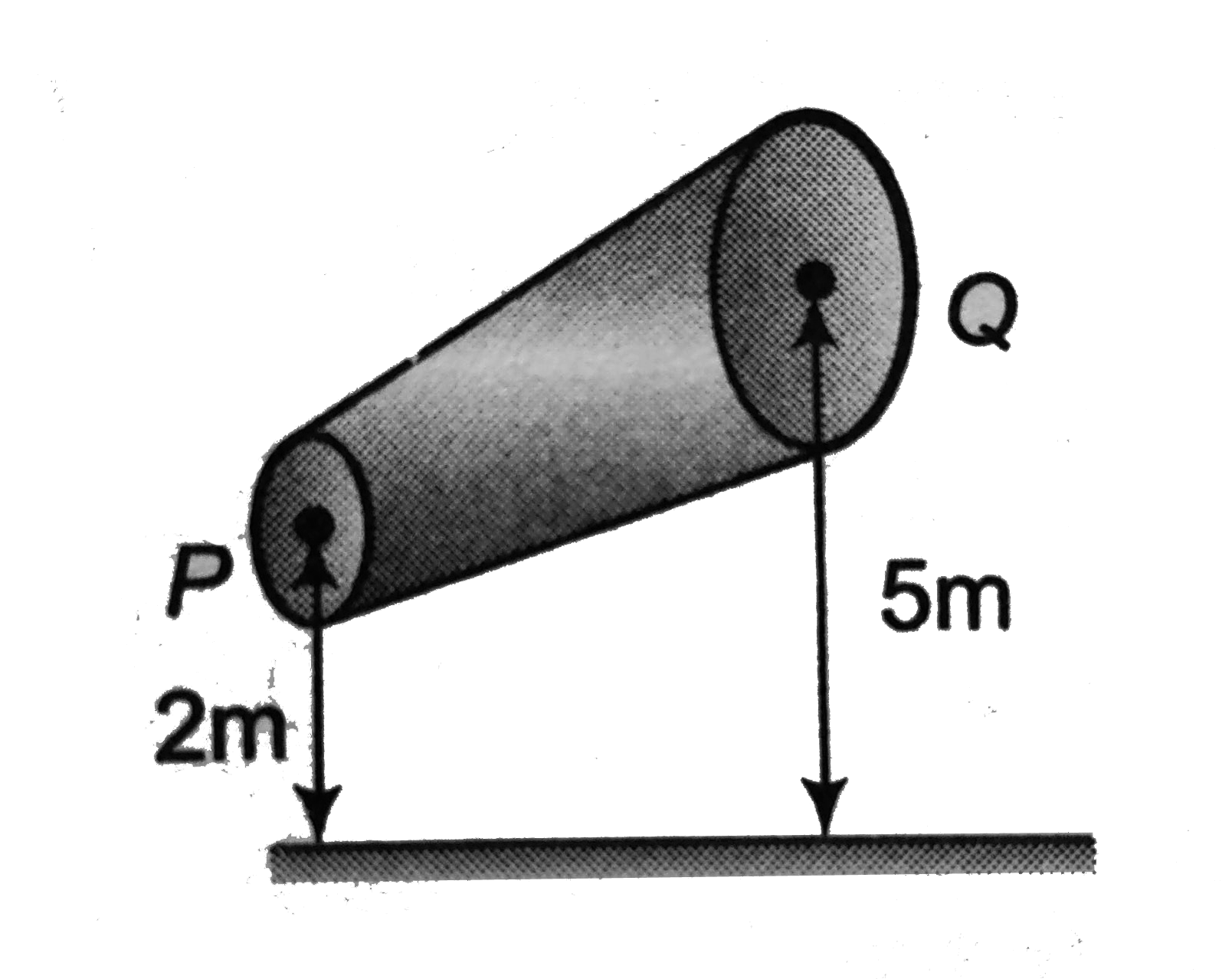
View Solution
Exercise- 2 PART - II questions and complete solutions for chapter FLUID MECHANICS of RESONANCE ENGLISH of Class 11
All Exercises from RESONANCE Class 11 PHYSICS FLUID MECHANICS
- Advanced Level Problems
- Board Level Exercise
- Examples
- Exercise
- Exercise- 1 PART - I Section (B)
- Exercise- 1 PART - I Section (A)
- Exercise- 1 PART - I Section (C)
- Exercise- 1 PART - II Section (A)
- Exercise- 1 PART - II Section (B)
- Exercise- 1 PART - II Section (C)
- Exercise- 2 PART - I
- Exercise- 2 PART - II
- Exercise- 2 PART - III
- Exercise- 2 PART - IV
- Exercise- 3 PART - I
- Exercise- 3 PART - II