Complete Solutions to गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न of chapter समतल रेखा में गति of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | समतल रेखा में गति |
| SANJEEV PUBLICATION | गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न |
| Number Of Questions | 26 |
| Academic Year | 2023-24 |
क्षैतिज घर्षण विहीन टेबिल के केंद्र पर स्थित खूंटी से l लंबाई की डोरी का एक सिरा बांधा गया है तथा दूसरे सिरे पर m द्रव्यमान का एक कण बांधा उसे v वेग से वृत्तीय गति करवाई जाती है कण पर केंद्र की ओर लगने वाला बल होगा (T डोरी में तनाव को दर्शाता है)
View Solutionएक कण 25 सेमी. त्रिज्या के वृत्त में 2 चक्कर /सेकण्ड की चाल से गति कर रहा है । कण का त्वरण `m//s^(2)` में होगा
View Solutionएक कर्ण 5 cm त्रिज्या के वृत्ताकार पथ में एक स्थिर चाल और 0.2 `pi` सेकण्ड के आवर्तकाल से घूर्णन कर रहा है। कण का त्वरण है
View SolutionR त्रिज्या के किसी ऊर्ध्वाधर पाश (लूप) में m द्रव्यमान के किसी पिण्ड को किस निम्नतम वेग से प्रवेश करना चाहिए कि वह पाश को पूर्ण कर सके
View Solution1.0 m लम्बी रस्सी का एक सिरा 0.5 kg द्रव्यमान की एक वस्तु में बंधा है यह 4 rad/s की कोणीय आवृत्ति से ऊर्ध्वीय वृत्त में घूम रहा है । जब वस्तु गति करते हुए निम्नतम बिंदु पर हो तो रस्सी का तनाव होगा (`g=10m//s^(2)` लेने पर)
View Solutionविरामावस्था में स्थित 50 सेमी. त्रिज्या की कोई एकसमान वृत्ताकार डिस्क अपनेक तल मे लम्बवत और केंद्र से गुजरने वाले अक्ष के पारतः घूमने के लिए स्वतंत्र है । इस डिस्क पर कोई बल आघूर्ण कार्य करता है जो इनमं 2.0 ras `s^(-2)` का नियम कोणीय त्वरण उत्पन्न कर देता है । 2.0 s के पश्चात `ms^(-2)` में इसका नेट त्वरण होगा लगभग
View Solution10 g द्रव्यमान का कोई कण 6.4 सेमी. लम्बी त्रिज्या के वृत्त के अनुदिश किसी नियम स्पर्श रेखीय त्वरण से गति करता है । यदि गति आरंभ करने के पश्चात दो परिक्रमाएं पूरी करने पर कण की गतिज ऊर्जा `8xx10^(-4)J` हो जाती है तो इस त्वरण का परिमाण क्या है
View Solutionचित्रानुसार R=2.5m त्रिजया के वृत्तीय पथ पर दक्षिणावर्त गति करते हुए किसी कण के कुल त्वरण को किसी क्षण `a=15m//s^(2)` से निरूपित किया जाता है । कण की चाल होगी-

View Solutionएक प्रक्षेप्य की अधिकतम ऊंचाई तथा क्षैतिज परास आपस में बराबर हैं तो प्रक्षेप्य का प्रक्षेपण कोण है
View Solutionसभी दिशाओं में v वेग से कई गोलियां दागी जाती हैं। पृथ्वी तल पर वह आधिकतम क्षेत्रफल क्या होगा जिस पर ये गोलियां फैल जायेगी।
View Solutionवह प्रक्षेपण कोण जिसके लिए प्रक्षेप्य की क्षैतिज परास तथा अधिकतम ऊंचाई बराबर होगी है
View Solutionएक m द्रव्यमान के कण को प्रारंभिक गति `u_(0)` से क्षैतिज से `alpha` कोण पर प्रक्षेपित किया जाता है। यह कण प्रक्षेप्य पथ के उच्चतम बिंदु पर एकसमान द्रव्यमान के कण के साथ पूर्णतः अप्रत्यास्थ संघट्ट करता है, जो कि भूतत से ऊर्ध्वाधर दिशा में समान प्रारंभिक गति `u_(0)` से फेंका गया था। संयुक्त निकाय संघट्ट के तत्काल बाद क्षैतिज से निम्न कोण बनाएगा।
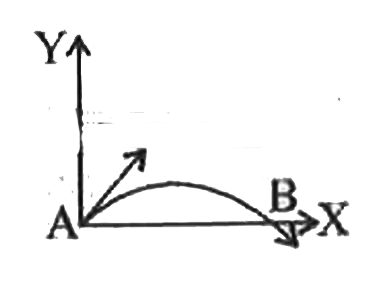
View Solutionकिसी प्रक्षेप्य का प्रारंभिक बिंदु A पर वेग `(2hati+3hatj)m//s` है तो इसका बिंदु B पर वेग (m/s में ) होगा
View Solutionएक वेग `barv=K(yhati+xhatj)` जहां K एक स्थिरांक है । इसके पथ का सामान्य समीकरण है
View Solutionएक प्रक्षेप्य को पृथ्वी की सतह से `5ms^(-1)` के वेग से तथा क्षैतिज दिशा से `theta` कोण पर छोड़ा जाता है। किसी अन्य से `3ms^(-1)` के वेग तथा इसी कोण `(theta)` पर छोड़े गये एक प्रक्षेप्य का प्रक्षेप पथ पृथ्वी से छोड़ गये एक प्रक्षेप्य पथ के सर्वसम (सर्वथा समान) है। यदि पृथ्वी पर `g=9.8ms^(-2)` है तो इस ग्रह पर गुरूत्वीय त्वरण का मान `ms^(-2)` में होगा
View Solutionयदि किसी समय पर किसी कण के x तथा y निर्देशांक क्रमशः `x=5t-2t^(2)` तथा `y=410t` है। (जहां x तथा y मीटर में और t सेकण्ड में है) तो `t=2s` पर उस कण का त्वरण होगा
View Solutionएक प्रसारी गोले की तात्क्षणिक त्रिज्या R एवं द्रव्यमान M अचर होते हैं। प्रसार के दौरान इसका तात्क्षणिक घनत्व `p` पूरे आयतन में एकसमान रहता है एवं आंशिक घनत्व की दर `(q/(rho) (dp)/(dt))` अचर है। इस प्रसारी गोले के पृष्ठ पर एक बिंदु पर वेग v निम्न के समानुपाती होगा
View Solutionएक त्रिविमीय निर्देशांक निकाय में गतिशील एक कण के स्थिति निर्देशांक निम्न हैं
`x=a cos omega t`
`y=a sin omegat`
तथा `z=a omegat`
इस कण की गति का मान होगा
View Solution`t=0` पर क्षैतिज से `60^(@)` के कोण पर `10ms^(-1)` के वेग से एक पिण्ड को प्रक्षेपित करते है। `t=1s` पर प्रक्षेप पथ की वक्रता त्रिज्या R है। वायु प्रतिरोध को नगण्य मानकर तथा गुरूत्वीय त्वरण `g=10ms^(-2)` लेकर R का मान है
View Solutionएक 60 m लंबी यात्री गाड़ी 80 km/hr की गति से चल रही है। 120 m लम्बाई की एक और मालगाड़ी 30 km/hr से चल रही है। ऐसे समयों का अनुपात जो यात्री गाड़ी को मालगाड़ी को पार करने में लगेंगे जब (i) गाड़ियां एक ही दिशा में जा रही हैं और (ii) गाड़ियां विरोधी दिशाओं में जा रही हैं होगा
View Solutionएक कण एक वृत्ताकार पथ पर `10ms^(-1)` की नियत गति से चल रहा है। जब यह कण वृत्त के केंद्र के परितः`60^(@)` चलता है तो इसके वेग में हुए परिवर्तन का परिमाण होगा
View Solution`r_(A)` और `r_(B)` त्रिज्याओं के संकेंद्री वृत्तों पर दो कण AB क्रमशः `v_(A)` और `v_(B)` वेगों से एकसमान वृत्तीय गति कर रहे हैं। इनके घूर्णन का आवर्तकाल समान है। A और B की कोणीय चालों का अनुपात होगा
View Solutionजब क्षैतिज से `60^(@)` कोण पर रखे किसी लंबे चिकने आनत तल की तली से किसी पिण्ड पर शॉट लगाया जाता है तो वह तल के अनुदिश `x_(1)` दूरी चल सकता है। परंतु जब झुकाव को घटाकर `30^(@)` कर दिया जाता है तथा इसी पिण्ड पर समान वेग से शॉट लगाया जाता है तब वह `x_(2)` दूरी चल सकता है । तब `x_(1):x_(2)` होगा
View Solutionएक गेंद को भूमि पर क्षैतिज तल से `45^(@)` के कोण पर प्रक्षेपित किया जाता है। गेंद `120m` की अधिकतम ऊंचाई पर पहुंच कर भूमि पर वापस लौट आती है । भूमि से पहली बार टकराने के उपरांत गेंद की गतिज ऊर्जा आधी हो जाती है। टकरानी के तुरंत बाद गेंद का वेग क्षैतिज तल से `30^(@)` का कोण बनाता है। टकराने के बाद गेंद................. मीटर की अधिकतम ऊंचाई पर पहुंचती है।
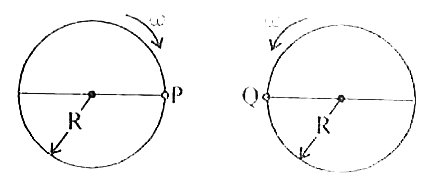
View Solutionसमान त्रिज्या R वाली दो एकसमान डिस्क अपनी धुरी पर एकसमान व स्थिर कोणीय चाल `omega` से विपरीत दिशा में घुम रही हैं। डिस्क एक ही क्षैतिज अनुसार आमने-सामने समय t=0 पर बिंदु P और Q चित्र में दर्शाये अनुसार आमने-सामने हैं। बिंदु P और बिंदु Q की आपेक्षिक चाल `V_(r)` को एक आवर्तकाल (T) में देखें। तब `V_(r)` का समय के साथ परिवर्तन का किस ग्राफ में सर्वोत्तम वर्णन है
View Solutionकिसी 240 m ऊंची चोटी के एक किनारेक से दो पत्थरों को एक साथ ऊपर की ओर फेंका गया है इनकी प्रारंभिक चाल क्रमशः 10 m/s तथा 40 m/s है, तो निम्नांकित में से कौन सा ग्राफ (आलेख) पहले पत्थर के सापेक्ष दूसरे पत्थर को स्थिति के समयन विचरण (परिवर्तन) को सर्वाधिक सही दर्शाता है।
मान लीजिए एक पत्थर जमीन से टकराने के पश्चात ऊपर की ओर नहीं उछलते हैं तथा वायु का प्रतिरोध नगण्य है दिया है `g=10m//s^(2)` (यहां ग्रापु केवल व्यव्सथा आरेख है और स्केल के अनुसार नहीं है)
View Solution
गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न questions and complete solutions for chapter समतल रेखा में गति of SANJEEV PUBLICATION of Class 11
All Exercises from SANJEEV PUBLICATION Class 11 PHYSICS समतल रेखा में गति
- अन्य महत्तवपूर्ण प्रश्न (अतिलघूत्तरात्मक प्रश्न)
- अन्य महत्तवपूर्ण प्रश्न (आंकिक प्रश्न)
- अन्य महत्तवपूर्ण प्रश्न (निबंधात्मक प्रश्न)
- अन्य महत्तवपूर्ण प्रश्न (बहुचयनात्मक प्रश्न)
- अन्य महत्तवपूर्ण प्रश्न (रिक्त स्थानों की पूर्ति कीजिएः)
- अन्य महत्तवपूर्ण प्रश्न (लघूत्तरात्मक प्रश्न)
- अन्य महत्तवपूर्ण प्रश्न (सत्य असत्य)
- अन्य महत्तवपूर्ण प्रश्न (सही मिलान कीजिए।)
- उदाहरण
- गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न
- पाठ्यपुस्तक के प्रश्न