Complete Solutions to Example of chapter MOTION IN ONE DIMENSION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN ONE DIMENSION |
| SL ARORA | Example |
| Number Of Questions | 62 |
| Academic Year | 2023-24 |
A car travels from A to B at 20 `kmh^(-1)` and form B to A at 40 `kmh^(-1)`. Calculate the average speed and average velocity of the car.
View SolutionA car travels first half distance between two places with a speed of 60 `kmh^(-1)`. What should be its speed for rest half of the distance so that its average speed becomes `90 kmh ^(-1)`?
View SolutionA body covers one-third of its journey with speed 'u' , next third with speed 'v' and the last third with speed 'w'. Calculate the average speed of the body during the entire journey.
View SolutionA particle traversed on third of the distance with a velocity `v_(0)`, the remaining part of the distance was covered with velocity `v_(1)` for half the time and with a velocity `v_(2)` for the remaining half of time. Assuming motion to be rectilinear, find the the mean velocity of the particle averaged over the whole time of motion.
View SolutionA man walks on a straight road from his home to a market ` 2.5 km` away with a speed of `5 km //h`. Finding the market closed, he instantly turns and walks back with a speed of `7.5 km//h`. What is the (a) magnitude of average velocity and (b) average speed of the man, over the interval of time (i) `0` to 30 min `. (ii) 0 to 50 min (iii) 0 to 40 min ?
View SolutionA car (A) is moving at `60 km h^(-1)` on a straight road, is ahead of car (B) moving in the same direction at `10 ms^(-1)`. Find the velocity of (A) relative to (B) and vice versa.
View SolutionA jet airplance travelling at the speed of ` 500 km ^(-1)` ejects its products of combustion at the speed of ` 1500 km h^(-1)` relative to the jet plane. What is the speed of the burnt gases with respect to observer on the ground ?
View SolutionA police van moving on a highway with a speed of `30 km h^(-1)` Fires a bullet at a thief's car speeding away in a same direction with a speed of `192 km h^(-1)`. If the muzzle speed of the buller is `150 m s^(-1)`, with what speed does the bullet hit thief's car? .
 .
.
View SolutionA long belt is moving horizontally with a speed of `5 km h^(-1)`. A child runs on this belt to and fro with a speed of `9 km//h` (w.r.t. bett) between his father and mother located `50 m` apart on the belt. For an observer on a stationalry plateform outsied, what is the
(a) speed of the chils runningin the derection of motion of the belt, (b) speed of thechaild runing opposite to thedirection of the belt, and (c ) time taken by the child in cases (a) and (b) ? Which of theanswers change, if motion is viewed by one of the parents ?gt
View SolutionTwo parallel rail tracks run north-south Train `A` moves north with a speed of `54 km h^(-1)` and train `B` moves south with a speed of `90 km h^(-1)`. What is the
a. relative velocity of `B` with respect to `A`?
b. relative of a monkey running on the roof of the train `A` against its motion (with its velocity of `18 km h^(1)` with respect to the train `A` ) as observed by a man standing on the ground?
View SolutionTwo trains 120 m and 80 m in length are running in opposite directions with velocities `42 km h^(-1)` and `30 kmh^(-1)`. In what time they will completely cross each other?
View SolutionTwo cars are moving in the same direction with the same speed `30 km//hr`. They are separated by a distance of `5 km`, the speed of a car moving in the opposite direction of it meets these two cars at an interval of `4` minutes, will be.
View SolutionTwo towns `A` and `B` are connected by a regular bus service with a bus leaving in either direction every `T` min. `A` man cycling with a speed of `20 km h^(-1)` in the direction `A` to `B` notices that a bus goes past him every `18 min` in the direction of his motion, and every `6 min` in the opposite direction. What is the period `T` of the bus service and with what speed (assumed constant )do the buses ply on the road?
View SolutionA boat covers certain distance between two spots on a river taking 4 hours going downstream and 6 hours going upstream. What time will be taken by the boat to cover same direction in still water?
View SolutionThe speed of a motor launch with respect to water in a stream is `8 ms^(-1)` while water current's speed is `3 m s^(-1)`. When the launch began travelling upstream, a float was dropped from it. After travelling a distance of `4.8 km` upstream, the launch turned back and caught up with the float. What is the total time which elapsed during the process?
View SolutionA race car accelerates on a straight road from rest to a speed of `180 kmh^(-1)` in 25s. Assuming uniform acceleration of the car throughout, find the distance covered in this time.
View SolutionA car moving along a straight highway with speed of `16 kmh^(-1)` is brought to a stop within a distance of 200 m. What is the retardation of the car (assumed uniform), and how long does it take for the car to stop?
View SolutionAn electron travelling with a speed of `5xx10^(3) ms^(-1)` passes through an electric field with an acceleration of `10^(12)ms^(-2)`. (i) How long will it take for the electron to double its speed ?(ii) What will be the distance covered by the electron in this time?
View SolutionA driver takes 0.20 s to apply the brakes after he sees a need for it. This is called the reaction time of the driver. If he ils driving a car at a speed of 54 km/h and the brakes cause a deceleration of `6.0 m/s^2`, find the distance travelled by the car after he sees the need to put the brakes on.
View SolutionA bullet travellling with a velocity of 16 m/s penetrates a tree trunk and comes to rest in 0.4 m. Find the time taken during the retardation.
View SolutionTwo trains ` A and B` of length `400 m` each are moving on two parallel tracks with a uniform speed of ` 72 km h^(-1)`
in the same direction with ` A` ahead of `B` .The driver of B decides to overtake A
and accelerates by 1m/s².if after 50s ,the guard of B just passes the driver of A , what was the original distance between them ?
View SolutionOn a two lane road , car (A) is travelling with a speed of `36 km h^(-1)`. Tho car ` B and C` approach car (A) in opposite directions with a speed of ` 54 km h^(-1)` each . At a certain instant , when the distance (AB) is equal to (AC), both being ` 1 km, (B) decides to overtake ` A before C does , What minimum accelration of car (B) is required to avoid and accident.
View SolutionOn a foggy day two drivers spot each other when they are just 80 meters apart. They are travelling at `27kmh^(-1)` and `60kmh^(-1)` , respectively. Both of them applied brakes retarding their cars at the rate of `5ms^(-2)` Determine whether they avoid collision or not.
View SolutionA hunderd metre sprinter increases her speed from rest uniformly at the rate of `1ms^(-2)` upto three quarters of the total run and covers the last quarter with uniform speed. How much time does she take to cover the first half and the second half of the run?
View SolutionA car starts from rest and accelerates uniformly for `10 s`to a velocity of `80 ms ^(-1)`. It then runs at a constant velocity and is finally brought to rest in `64 m` with a constant retardation. The total distance covered by the car is `584 m` Find the value of acceleration, retardation, and total time taken.
View SolutionAn athlete runs a distance of 1500m in the following manner. (i) Starting from rest, he accelerates himself uniformly at `2ms^(-2)` till he covers a distance of 900m. (ii) He, then runs the remaining distance of 600m at the uniform speed developed. Calculate the time taken by the athlete to cover the two parts of the distance covered. Also find the time, when he is at the centre of the track.
View SolutionA body starting from rest accelerates uniformly at the rate of `10cms^(-2)` and retaeds uniformly at the rate of `20cms^(-2)` . Find the least time in which it can complete the journey of 5km if the maximum velocity attained by the body is `72kmh^(-1)` .
View SolutionA man is l=9 m behind the door of a train when it starts moving with acceleration a=`2 m//s^2`.The man runs at full speed. How far does he have to run and after what time does he get into the train ? What is his full speed ?
View SolutionA body moving with uniform acceleration, covers a distance of `20` m in the `7^(th)` second and `24 m` in the `9^(th)` second. How much shall it cover in `15^(th)` second?
View SolutionA body covers 12m in 2nd second and 20m in 4th second. How much distance will it cover in 4 seconds after the 5th second ?
View SolutionTwo busses A and B are at positions 50m and 100m from the origin at time t=0. They start moving in the same direction simultaneously wi8th uniform velocities of `10ms^(-1)` and `5ms^(-1)` . Determine the time and position at which A overtakes B.
View SolutionAn object is moving along +ve x-axis with a uniform acceleration of `4ms^(-2)` . At time t=0 , x=5m and `v=3ms^(-1)` .
(a) What will be the velocity and position of the object at time t=2s?
What will be the velocity and position of the object when it has a velocity of `5ms^(-1)`?
View SolutionA body is thrown vertically upwards with a velocity of `98ms^(-1)` Calculate (i) the maximum height reached (ii) the time taken to reach the highest point (iii) the velocity at a heighest of 196m from the point of projection (iv) the velocity with which it returneds to the ground and (v) the time taken to reach the ground.
View SolutionA ball throuwn vertically upwards with a speed of `19.6ms^(-1)` from the top of a tower returns to the earth in 6s. Find the height of the tower.
View SolutionA ball throuwn up is cautght by the thrower after 4s. How did it go and with what velocity was it thrown ? How far was it below the highest point 3s after it was thrown?
View SolutionA balloon is ascending at the rate of `9.8 m//s` and is 39.2 m above the ground when a package is dropped. (a) How long does the package take to reach the ground? (b) with what speed does it hit the ground ? `(g = 9.8 m//s^(2))`
View SolutionA food packet is released from a helicopter which is rising steadily at `2ms^(-1)` , After two second (i) What is the velocity of the packet ? (ii)How far is it below the helicopter?
Take `g=9.8ms^(-2)` .
View SolutionA parrachutist bails out from an aeropane and after dropping through a distance of `40 m` opens the parachute and decelerates at `2 ms^(-2)`. If he reaches the ground with a speed of `2 ms^(-1)`, how lowg he in the air ? At what height did he bail out from the plane ?
View SolutionTwo balls are thrown simultaneously, A vetically upwards with a speed of `20 ms^(-1)` from the ground, and B vetically downwards from height of 40 m with the same speed and along the same line of motion. At what points do the two balls collide? Take `g= 9.8 ms^(-2)`.
View SolutionA stone falls from a cliff and travels 24.5 m in the last second before it reaches the ground at the foot of the cliff. Find the height of the cliff.
View SolutionA stone is dropped from the top of a tower of height `h`. Aftre `1 s` another stone is droppped from the balcony `20 m` below the top. Both reach the bottom simultaneously. What is the value of `h` ? Take `g=10 ms^(-2)`.
View SolutionA stone is dropped into a well `45 m` deep. The sound of the splash of the splash is heard `3.13 s` after the stone is dropped. Find the speed of sound in air. Take `g = 10 m//s^2`.
View SolutionThe acceleration due to gravity on a planet is `1.96 ms^(-1)`. If it is safe to jump from a height of 2 m on the earth, what will be the corresponding safe height on the planet?
View SolutionA boy standing on a stationary lift ( open from above ) throws a ball upwards with the maximum initial speed he can, equal to ` 49 ms^(-1)`. How much time does the ball take to return to his hands ? If the lift starts moving up with a uniform speed of ` 5 ms^(-1)` and the boy again throws the ball up with the maximum speed he can , how hoes the ball take to return to his hands ?
View SolutionA player throwsa a ball upwards with an initial speed of `29.4 ms^(-1)`.
(i) What is the direction of acceleration during the upwared motion of the ball?
(ii) What are the velocity and acceleration of the ball at the highest point of its motion?
(iii) Choose the x=0 and t=0 to be the location and time of the ball at its highest point, vertically downward direction to be the positive direction of X-axis, and give the signs of positive, velocity and acceleration of the ball during its upward, and downward motion.
(iv) To what height does the ball rise and after how long does the ball return to the player's hand?( Take g`=9.8 ms^(-2)`, and neglect air resistance).
View SolutionA stone is dropped from rest from a point 0.4 m above a window 0.5m high. Find the time taken by the stone to pass against window.
View SolutionThe displacement x of a particle varies with time t as
`x=4t^(2)-15t+25`
Find the position, velocity and acceleration of the particle at t=0. When will the velocity of the particle become zero? Can we call the motion of the particle as one with uniform acceleration ?
View SolutionThe velocity of a paticle is given by the equation, `v=2t^(2)+5cms^(-1)`. Find (i) the change in velocity of the velocity of the particle during the time interval between `t_(1)=2s` and `t_(2)=4s` (ii) the average acceleration during the same interval and (iii) the instantaneous acceleration at `t_(2)=4s`.
View SolutionThe distance x of a particle moving in one dimensions, under the action of a constant force is related to time t by the equation, `t=sqrt(x)+3`, where x is in metres and t in seconds. Find the displacement of the particle when its velocity is zero.
View SolutionThe position-time (x-t) graphs for two children `A` and `B` returning from their school `O` to their homes `P` and `Q`, respectively, are shown in . Choose the
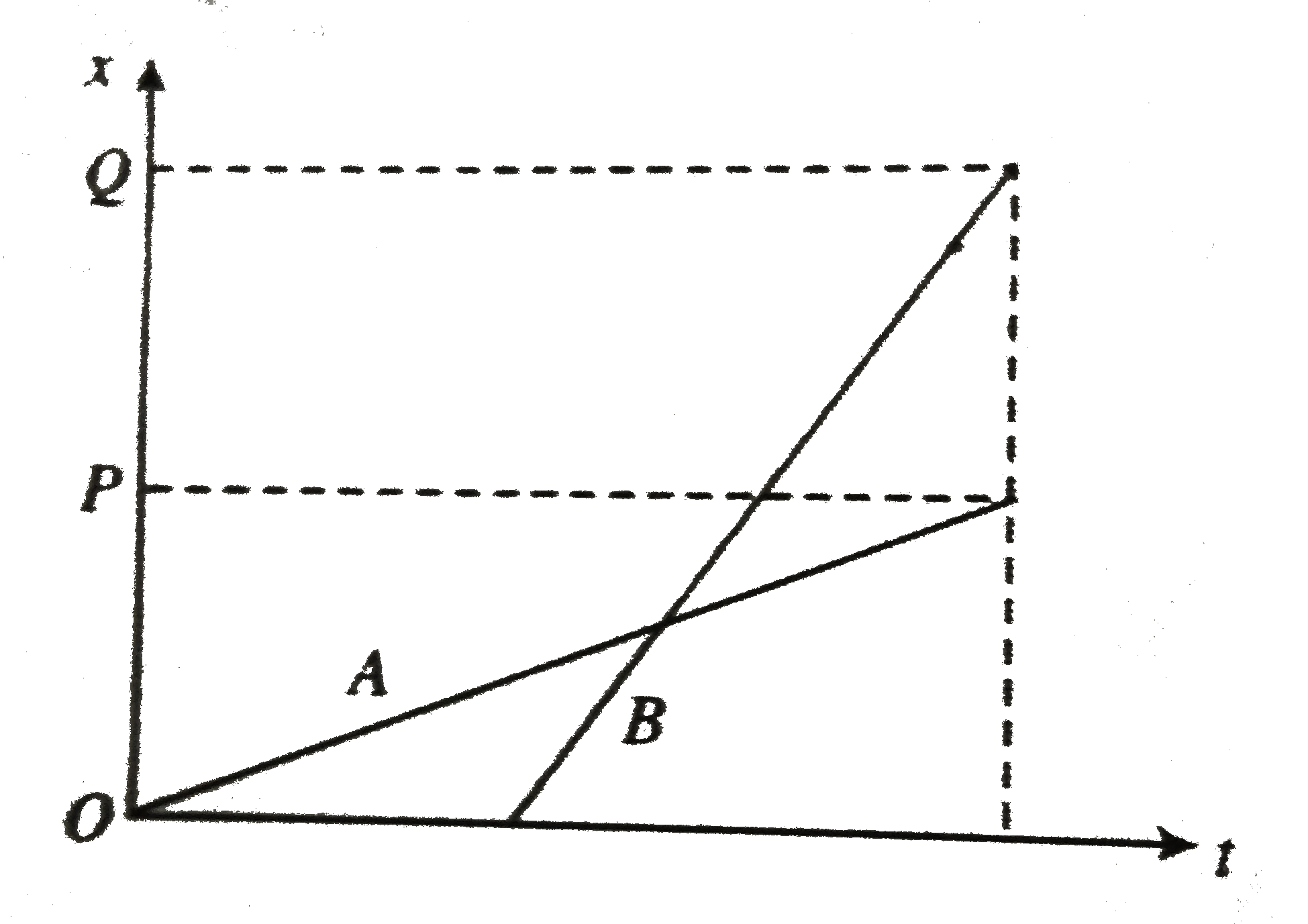 .
.
a.` (A//B)` Iives closer to school than `(B//A)`.
b. `(A//B)` starts from the school earlier than `(B//A)`.
c. `(A//B)` walks faster than `(B//A)`.
d. `A` and `B` reach home at the (same//differnt) time.
e. (A//B) overtakes on the road (once//twice).
View SolutionTwo straight lines drawn on the same velocity-time graph make angles ` 30^(@)` and `60^(@)` with time axis respectively, as shown in Fig. Which line represents greater acceleration ? What is the ratio of the two accelerations ?
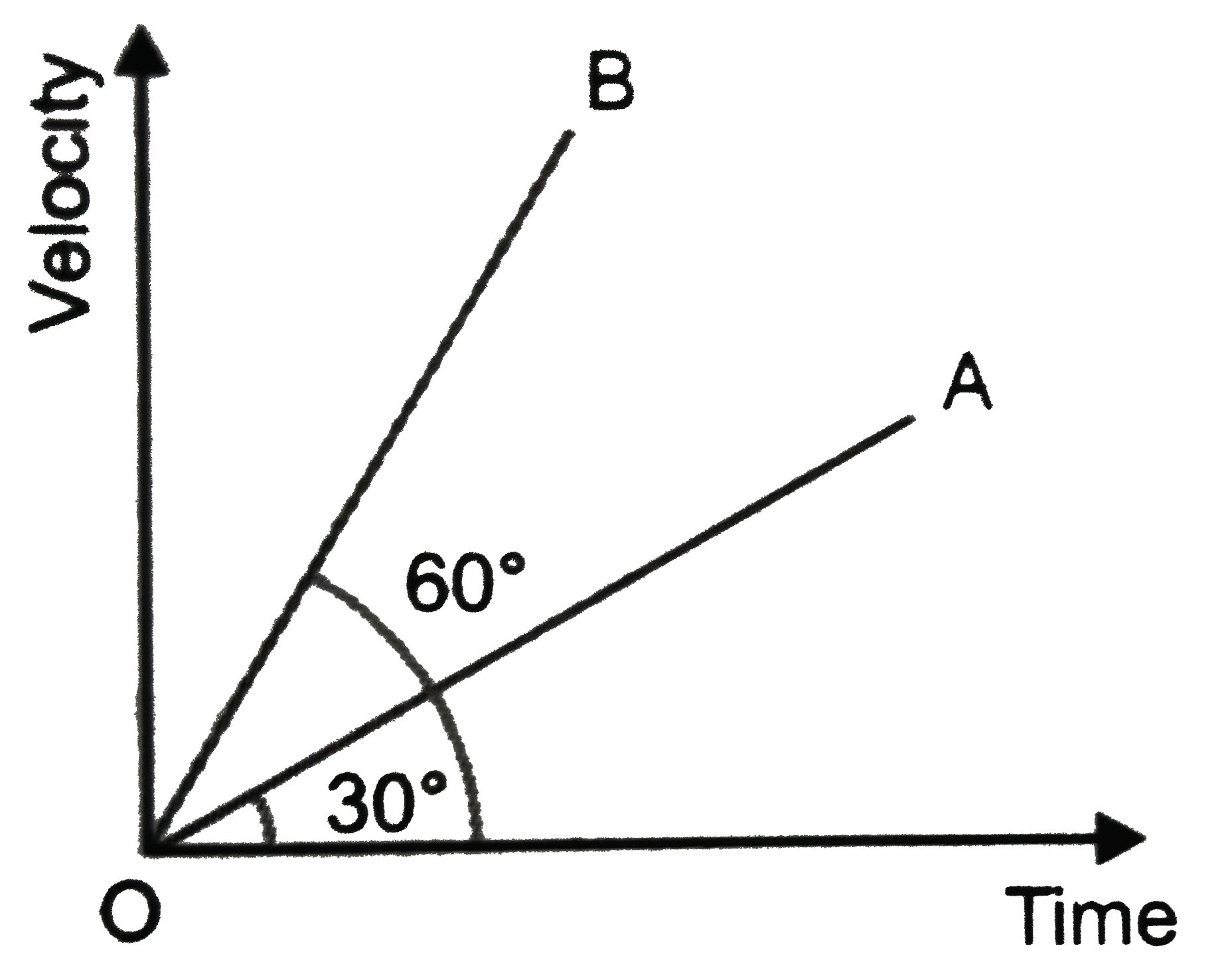 .
.
View SolutionA woman starts from her home at `9.00` a. m., walks with a speed of `5 km h^(-1)` on straight road up to her office `2.5 km`away, stays at the office up to `5.00 p. m.`, and returns home by an auto with a speed of `25 kmh^(-1)`. Plot the position-time graph of the woman taking home as origin.
View SolutionA drunkard walking in a narrow lane takes 5 steps forward and 3 steps backward, followed again by 5 steps forward and 3 steps backward, and so on. Each step is `1m` long and requires 1s. Plot the x-t graph of his motion. Determine graphically or otherwise how long the drunkard takes to fall in a pit 9 m away from the start.
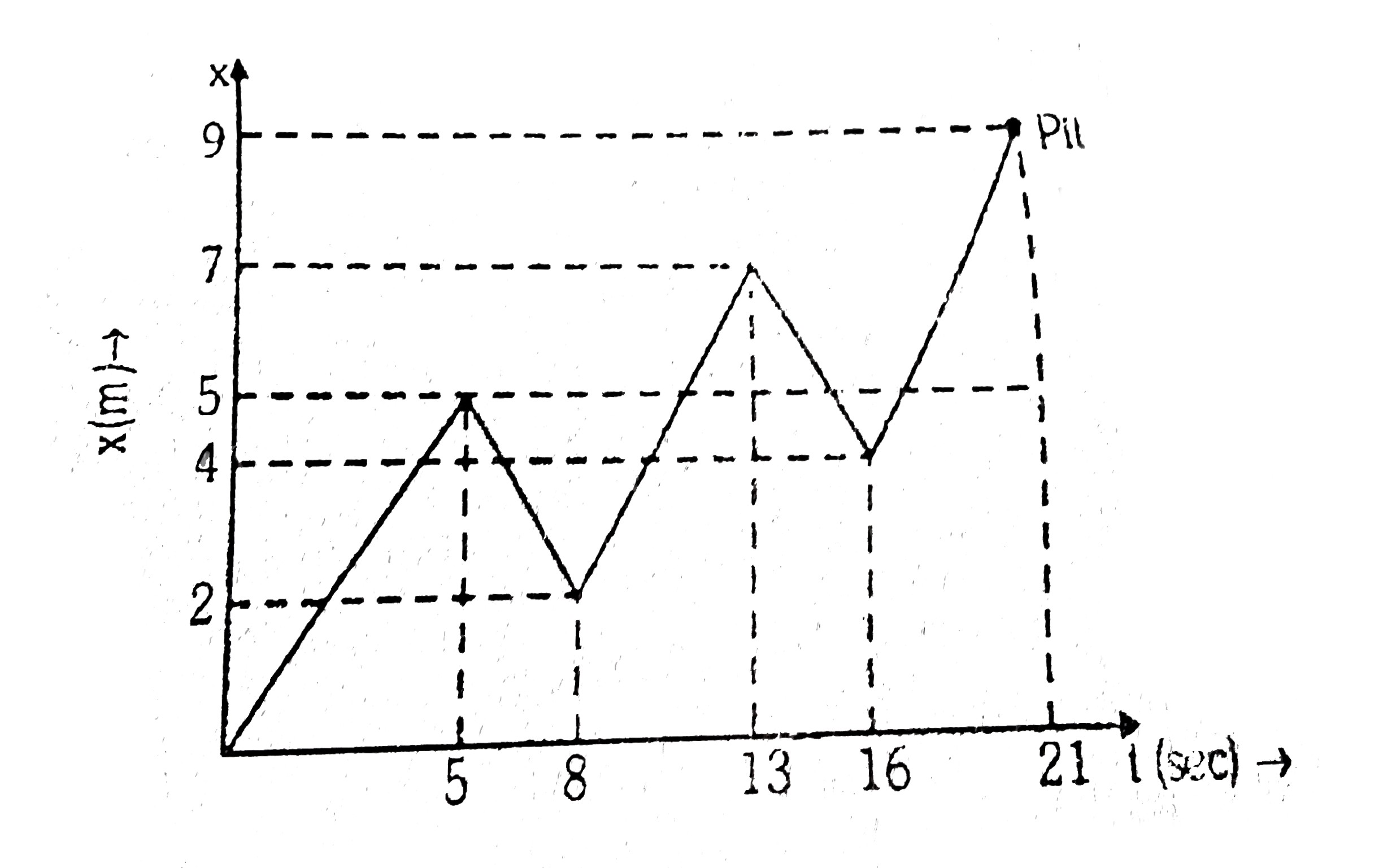
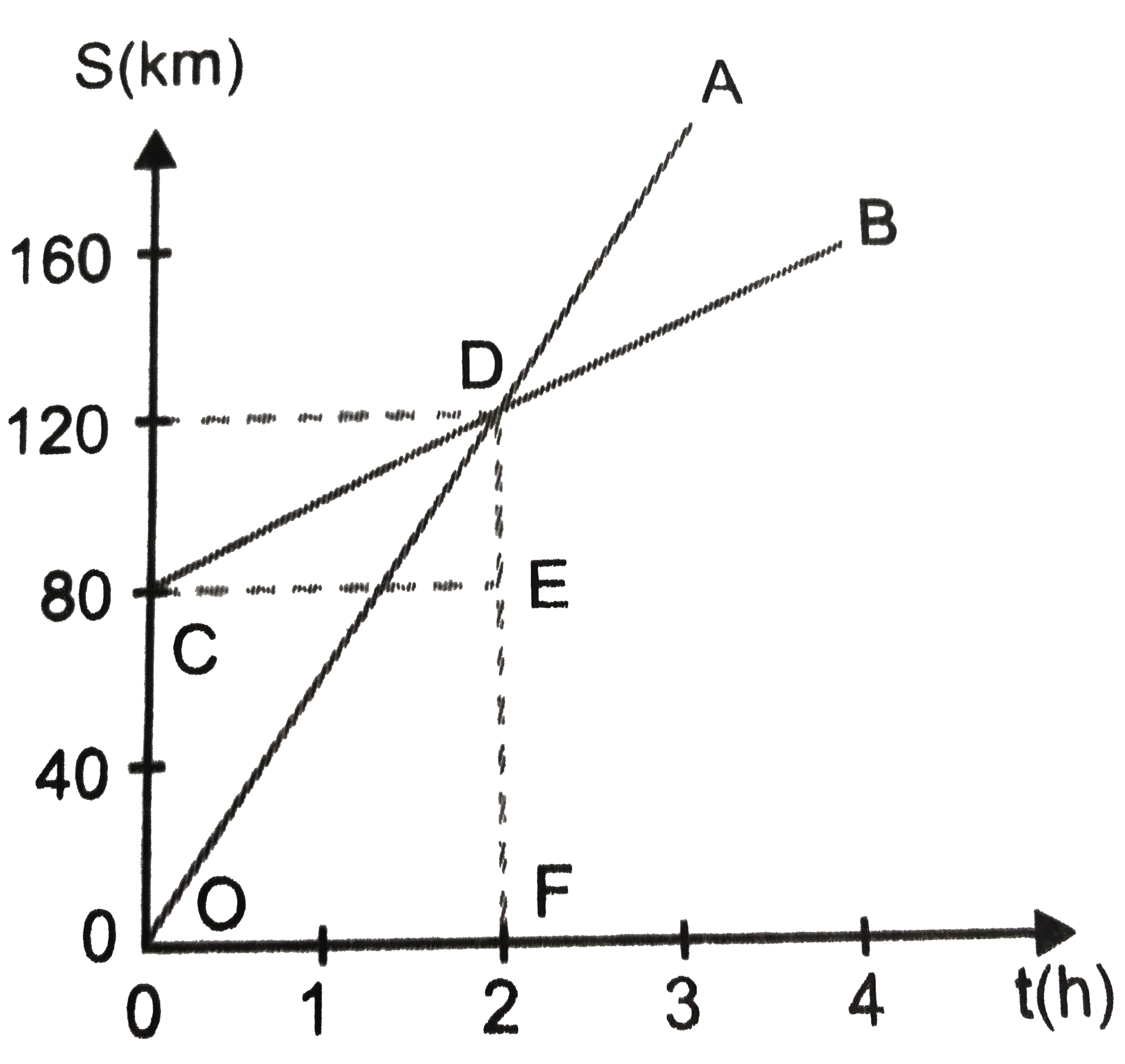
View SolutionFig. 2 (b). 12` shows thae distance (S) -time (t) graphs of two trains, which start moving simultaneously in the same direetion. From the graphs, find:
 .
.
(a) How much (B) is ahead of (A) when motion starts
(b) What is the speed of (B) ?
( c) What and where (A) will catch (B) ? `
(d) What is the differnce in speeds of (A) and (B) ? lt
View SolutionStarting from rest a car moves with uniform acceleration and attains a velocity of `72 kmh^(-1)` in 15 s. It then moves with uniform speed for 20s and is then brought to rest in 10 s undere uniform retardation. Find total distance travelled using velocity - time graph.
View SolutionA train starting from rest accelerates uniformly for 100s, runs at a constant speed for 5 minutes and then comes to a stop with uniform retardation in next 150 seconds. During this motion, it covers a distance of 4.25 km. Find its (i) constant speed (ii) acceleration and (iii) retardation
View SolutionA train moves from one station to another in two hours time. Its speed during the motion is shown in the graph Calculate
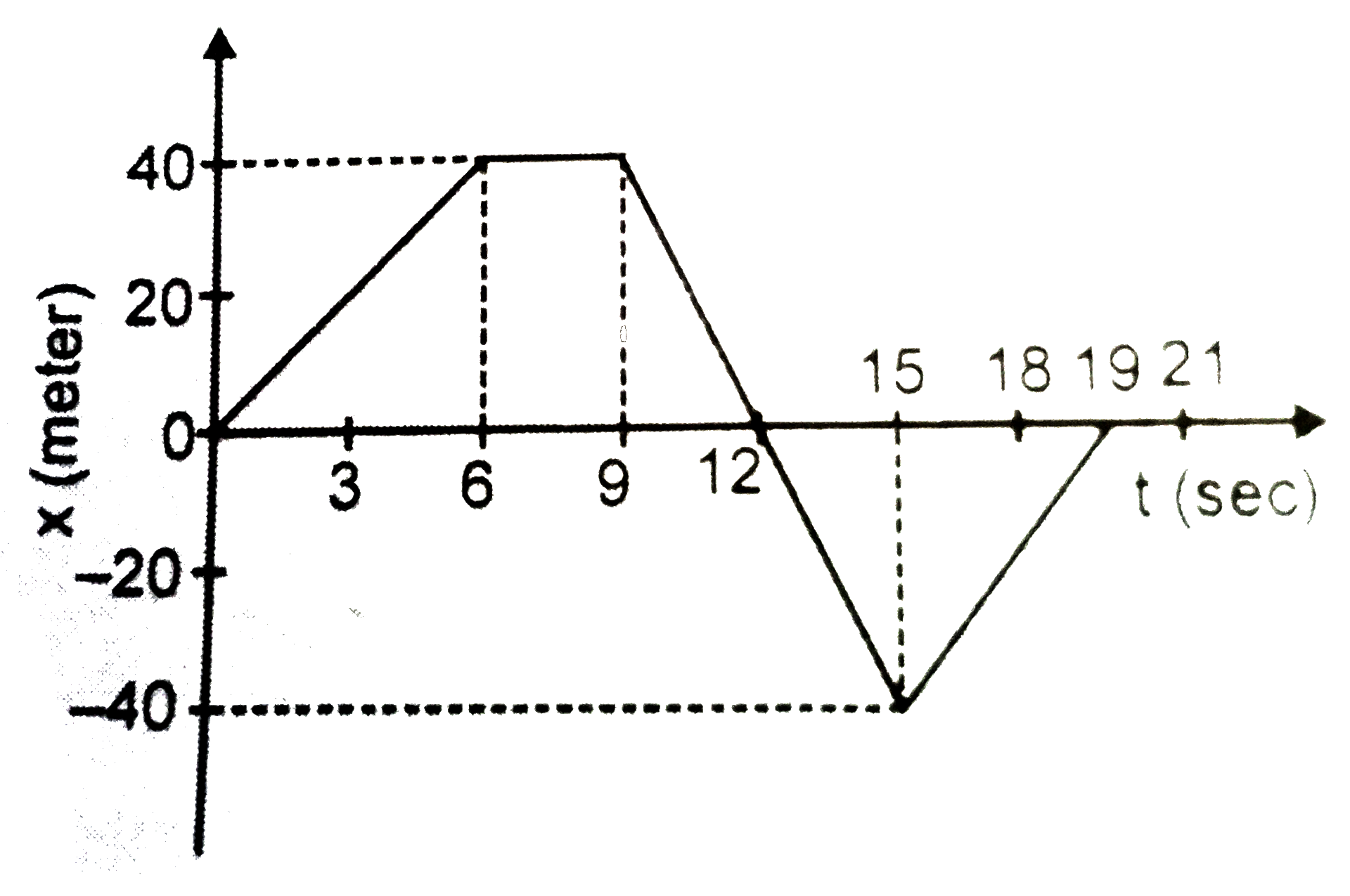
(i) Maximum acceleration during the journey.
(ii) Distance covered during the time interval from 0.75 hour to 1 hour
View SolutionA three wheeler starts from rest, accelerates uniformly with ` 1 ms^(-2)` on a straight road for ` 10 s` and then moves with uniform velocity . Plot a graph between the distance covered by the vehicle during the nth second ( n = 1,2,3, ……..) versus (n) What do you expect the plot to be during accelerated motion: a straight line or a parabola ?
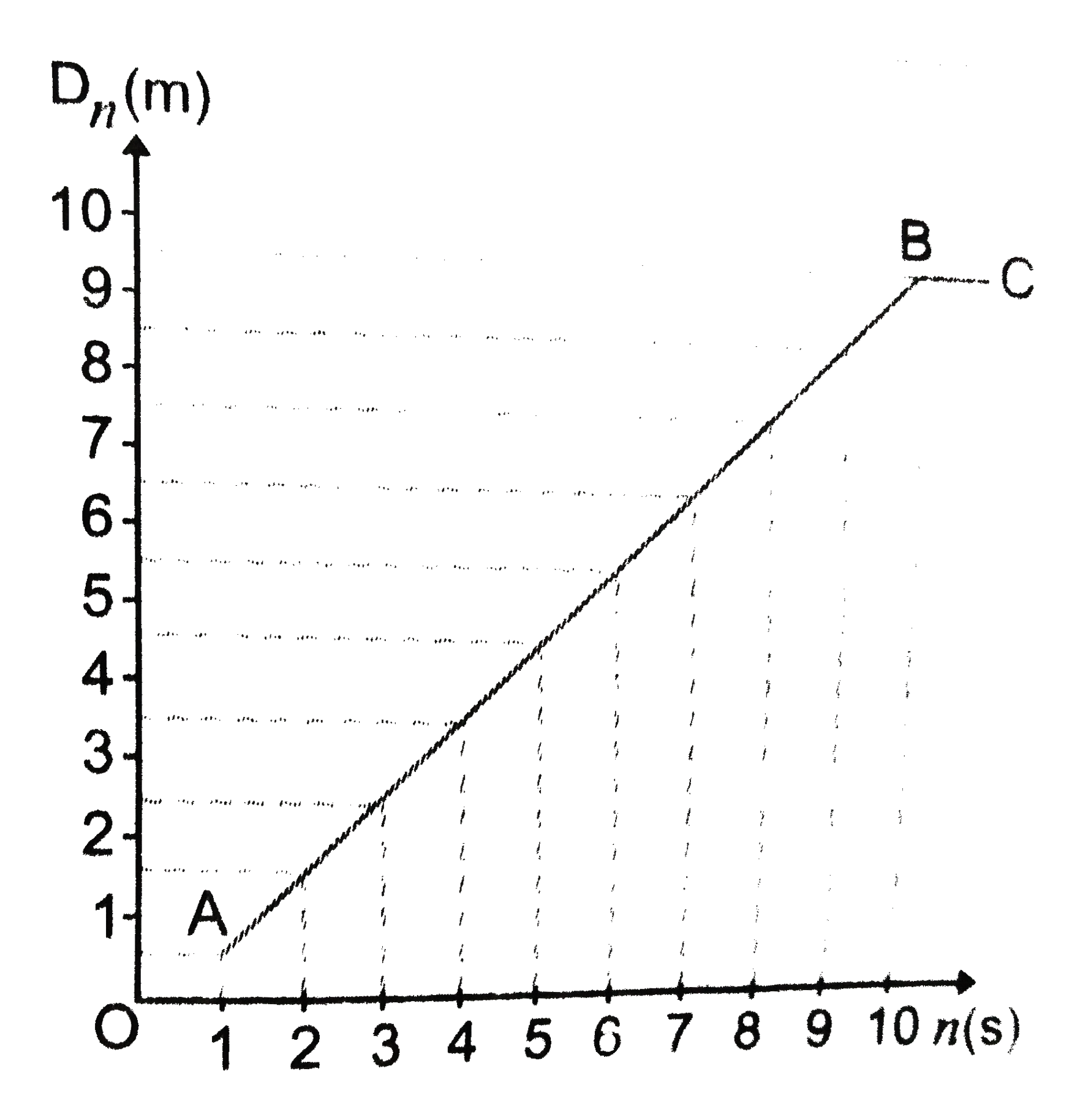 .
.
View SolutionA ball is throwm upword with an initial velcoity o f`100 ms^(-1)`. After how much time will it retun ? Draw velcoity - time graph for the ball and find from the graph (i) the maximum height attained by the ball and (ii) height of ball after 15 s. take g = `10 ms ^(-2)`.
View SolutionA ball is dropped from a height of a height of 90 m on a floor. At each collsion with the floor , the ball loses one - tenth of its speed . Plot the speed -time graph of its motion between t 0 to 12 s.
View SolutionTwo stones are thrown up simultaneously from the edge of a cliff ` 200 m` high with initial speeds of ` 15 ms^(-1)` and ` 30 ms^(-1)`. Verify that the graph shown in Fig. 2 ( NCT). 13 , correctly represents the time variation of the relative position of the second stone with respect to the first. Neglect the air resistance and assume that the stones do not rebound after hitting the ground. Take ` g= 10 ms^(-2)`.Give equations for the linear and curved parts of the plot.
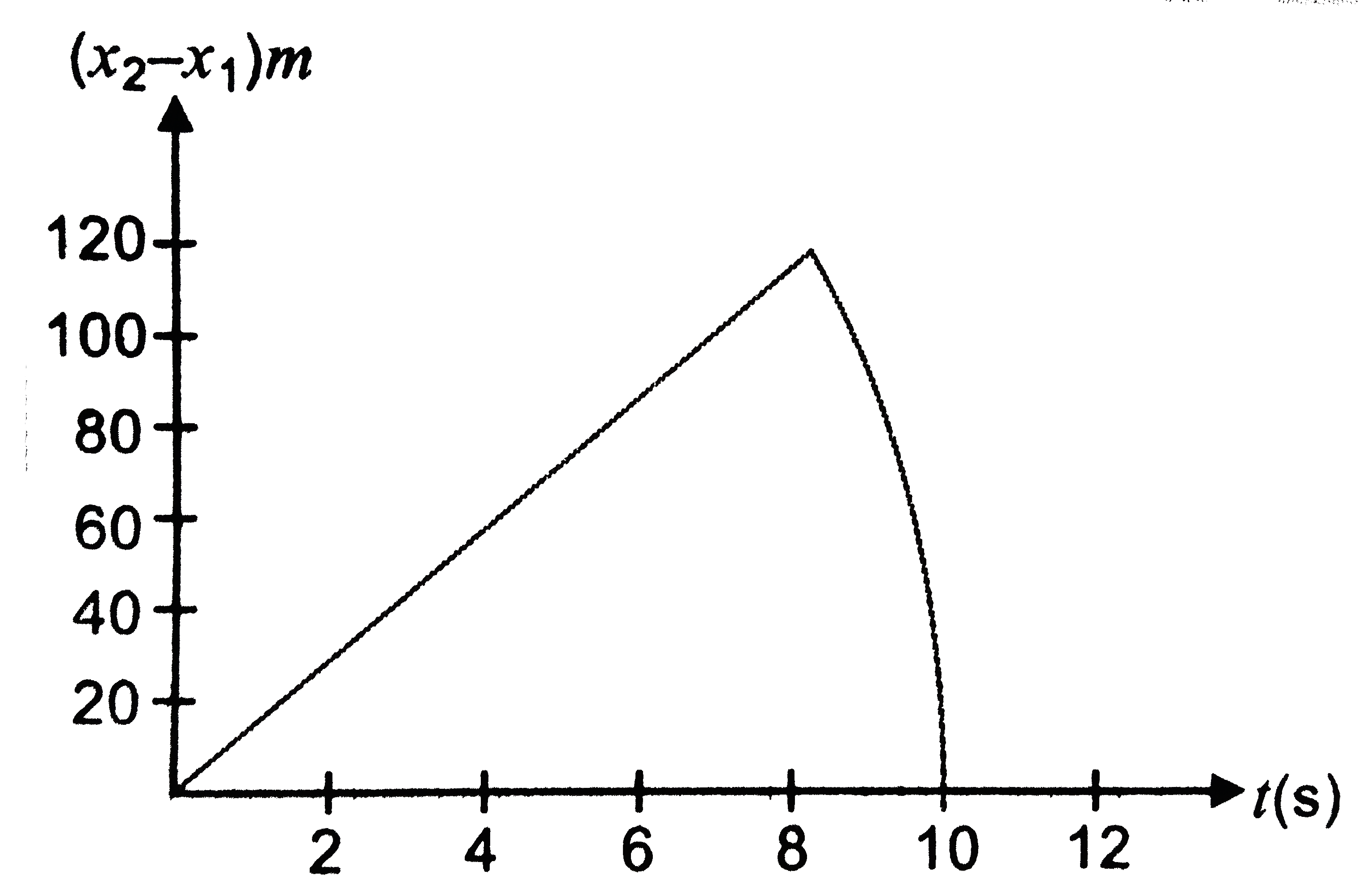 .
.
View Solutionthe velcoity - time graph for a vehicle is shown if fig 3.24. drow acceleration - time graph from it .
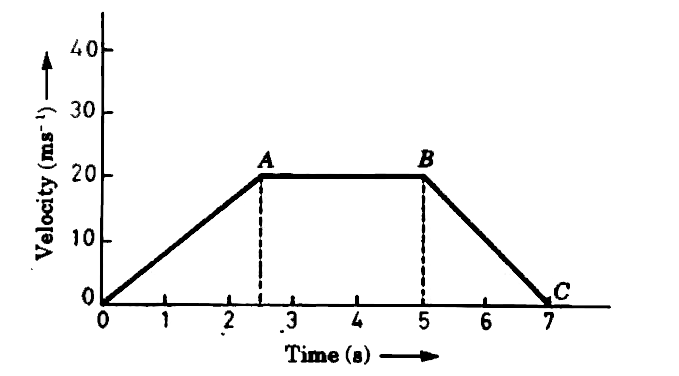
View Solution
Example questions and complete solutions for chapter MOTION IN ONE DIMENSION of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11