Complete Solutions to problem of chapter MOTION IN ONE DIMENSION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | MOTION IN ONE DIMENSION |
| SL ARORA | problem |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
the velcoity -time relation of an electron starting from rest is given by v=kt,where `h=2 ms^(-2)`.calculate the distance traversed in 3s.
View SolutionThe relation between time t and displacement x is `t = alpha x^2 + beta x,` where `alpha and beta` are constants. The retardation is
View SolutionThe deceleration exerienced by a moving motor blat, after its engine is cut-off is given by `dv//dt=-kv^(3)`, where `k` is constant. If `v_(0)` is the magnitude of the velocity at cut-off, the magnitude of the velocity at a time `t` after the cut-off is.
View SolutionA point moves with uniform acceleration and `v_(1), v_(2)`, and `v_(3)` denote the average velocities in the three successive intervals of time `t_(1).t_(2)`, and `t_(3)` Which of the following Relations is correct?.
View SolutionTwo trains are headed towaads each other on the same straight rrach, each vaving a speed of ` 30 km h^(-1)`. A bird that can fly at ` 60 km h^(-1)` flies off one train when they are ` 60 km` apart and leads firectly form the otjer train, On reaching the other train, tg flies back to the first train and so on.
(a) How many trips can the bird make from one trin to the other train befre they meet ? (b) What is the total distance the bird travels ?
View SolutionIn a car race, `A` takes a time of `t` s, less than car `B` at the finish and passes the finishing point with a velocity `v` more than car `B`. Assuming that the cars start from rest and travel with constant accelerations `a_(1)` and `a_(2)`. Respectively, show that `v=sqrt(a_(1) a_(2)t)`.
View SolutionThe driver of a train moving at a speed ` v_(1)` sights another train at a disane ` d`, ahead of him moving in the same direction with a slower speed ` v_(2)`. He applies the brakes and gives a constant teradation ` a` to his train. Show that here will be no collision if ` d gt (v_(1) -v_(2))^(2) //2 a`.
View SolutionA particle is moving in a straight line with constant acceleration. If x,y and z be the distances described by a particle during the pth, qth and rth second respectively, prove that
View SolutionA car accelerates from rest at a constant rate `alpha` for some time, after which it decelerates at a constant rate `beta,` to come to rest. If the total time elapsed is t seconds. Then evalute (a) the maximum velocity reached and (b) the total distance travelled.
View Solutionthe velcoity of a trian incrreases at a constant rate `alpha` from 0 to v and then remains constant for same interval and then finally decreases to zero at constant rate `beta`.if the total distance coverd by the the particle x,then show that the total time taken will be
`tx/v+v/2[1/alpha + 1/beta]`.
View SolutionA left storing from rest assends with constants acceleration 'a', then with a constant velcoity and finally stops under a constant retardation 'a'. If the total distance assended is 'x' and the total time taken is 't',show that the time during which the left is assending with constant vlocity is
`sqrt(t^(2)-(4x)/a`
View SolutionA body falling freely from a given height `H` hits an inlclined plane in its path at a height `h`. As a result of this impact the direction of the velocity of the body becomes horizontal. For what value of `h//H`, the body will take the maximum time to reach the ground.
View SolutionA rocket is fired vertically up from the ground with a resultant vertical acceleration of `10 m//s^2.` The fuel is finished in 1 min and it continues to move up. (a) What is the maximum height reached? (b) Afte2r how much time from then will the maximum height be reached?(Take `g= 10 m//s^2`)
View SolutionA body projected vertically upwords from the top of a tower reaches the ground in `t_(1)` second . If it projected vertically downwards from the some top with same velocity ,it reaches the ground in `t_(2)`seconds . If it is just dropped from the top it reaches the ground in t second .prove that `t=sqrt(t_(1)t_(2))`
View SolutionA particle is projected vertically upwards from a point O on the ground. It takes time `t_(1)` to reach a point `A` at a height h above the ground, it continues to move and takes a time `t_(2)` to reach the ground. Find (a) h, (b) the maximum height reached and (c ) the velocity of the partical at the half of maximum height.
View Solutionwater drops trickle out from a nozzle and fall on the height 4.0 m below at regular intervals. When first drop reaches the floor, the fifth drop begins to fall. Find the positive of the drops , when a drop just strikes the floor.
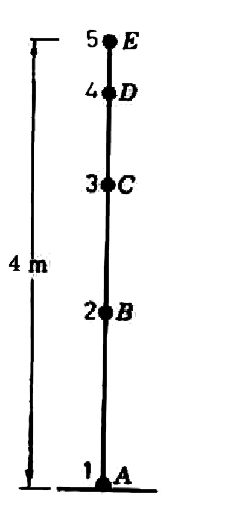
View SolutionA juggle maintains four balls in motion making each in turn rise to a height of 20 m form his hand. With velcoity does he project them and where will the other three ball be at the instant when the fourth one is just leaving the hand ? Take g = `10m^(-2)`
View SolutionA metal ball is allowed to fall freely on a perfectly elastic plate from a height 3 to ,At t= 0 the speed of the ball is zero. Diagrammatically repersent velocity with time specifying the proper unit on X and Y axes .
View SolutionA ball is dropped from a height of 19.6 m above the ground. It rebounds from the ground and raises itself up to the same height. Take the starting point s the origin and vertically downward as the positive X-axis. Draw approximate plots of x versus t, v versus t and a versus t. Neglect the small interval during which the ball was in contact with the ground.
View Solution
problem questions and complete solutions for chapter MOTION IN ONE DIMENSION of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11