Complete Solutions to Excercise of chapter Motion in a Plane of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | Motion in a Plane |
| SL ARORA | Excercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Which of the following quantities are independent of the choice of orientation of the coordinate axes : `vec a +vec`, `3a_x + 2b_y`, `|vec a +vec b- vec c|`, angle between `vec b` and `vec c` , `lambda vec a` , where `lambda` is a scalar ?
View SolutionAre the commutative law and associtive law applicable to vectors subtraction.
View SolutionCan three vectors not in one phane giv e a zero resultant ? Can four vectors do ?
View SolutionWhat is the differnce between the follwing data ? (i) 3 (`5 km h^(-1)` , west ) (ii) 3 hour (`5 km h^(-1)`, west).
View SolutionWhat was the difference between the speed of vehicle `A` on Day 1 and the speed of vehicle `C` on the same day? (a) 7 km/hr (b) 12 km/hr (c) 11 km/hr (d) 8 km/hr (e) None of these
View SolutionIs ` | vec A + vec B|` greater than or less than ` |vec A| + |vec B| `? Explain.
View SolutionIs ` |vec A - vec B|` greater than or less than ` |vec A| + |vec B|` ? Explain.
View SolutionWhat is the property of two vectors ` vec A and vec B`, if ` | vec A+ vecB| = | vec A- vec B|`.
View SolutionThe sum and differnce of two vectors are perpendicular to each other. Prove that the vectors are equal in magnitude.
View SolutionFind the condition for two vectors to be (i) paraiiel.
View SolutionIf `veca=x_1veci+y_1vecj and vecb=x_2veci+y_2vecj`, find the condition that would make them (i)perpendicular to each other, (ii)parallel to each other.
View SolutionIf `|vec P xx vec Q|=PQ` then the angle between `vec P and vec Q` is
View SolutionThe magnitude of vector `vec A` is 2.5 metre and is directed towards east. What will be the magnitudes and directions of the following: `-vec A`
View SolutionThe magnitude of vector `vec A` is 2.5 metre and is directed towards east. What will be the magnitudes and directions of the following: `(vec A)/2`
View SolutionThe magnitude of vector `vec A` is 2.5 metre and is directed towards east. What will be the magnitudes and directions of the following: `2.5 vec A`
View SolutionThe magnitude of vector `vec A` is 2.5 metre g and is directed towards east. What will be the magnitudes and directions of the following: `4 vec A`
View SolutionA person sitting in an open car moving at constant velocity throws a ball vertically up into air. The ball falls
View SolutionA person sitting in an open car moving at constant velocity throws a ball vertically up into air. The ball falls
View SolutionA bob hung from the ceiling of a room by a string is performing simple harmonic oscillations. What will be the trajectory of the bob, if the string is cut. When bob is (i) at one of its extreme positions (ii) at its mean position ?
View SolutionA bob hung from the ceiling of a room by a string is performing simple harmonic oscillations. What will be the trajectory of the bob, if the string is cut. When bob is (i) at one of its extreme positions (ii) at its mean position ?
View SolutionProve that the horizontal range is same when angle of projection is (i) greater than ` 45^(@)` by certain value and (ii) less than ` 45^(@)` by the same value.
View SolutionProve that the horizontal range is same when angle of projection is (i) greater than ` 45^(@)` by certain value and (ii) less than ` 45^(@)` by the same value.
View SolutionTwo bombs of ` 2 kg and 4 kg are thrown from a canon with the same velocity in the same direction. Which bomb will reach the ground first ?
View SolutionTwo bombs of 5 kg and 10 kg are thrown from a cannon with the same velocity in the same direction,If the bombs are thrown in the same direction with different velocity, what would be the effect ?
View SolutionTwo bodies are thrown with the same initial velocity at angles ` theta` and `(90^(@)- theta)` with the horizontal. What will be the ratio of (ii) maximum heights attained by them and (ii) of horizontal ranges ?
View SolutionTwo bodies are thrown with the same initial velocity at angles ` theta` and `(90^(@)- theta)` with the horizontal. What will be the ratio of (ii) maximum heights attained by them and (ii) of horizontal ranges ?
View SolutionAt which point of projectile motion (i) potential energy is maximum (ii) kinetic energy is maximum (iii) total mechanical energy is maximum.
View SolutionAt which point on the projectile trajectory is the (ii) kinetic energy minimum.
View SolutionAt which point of projectile motion (i) potential energy is maximum (ii) kinetic energy is maximum (iii) total mechanical energy is maximum.
View SolutionA body A of mass m is thrown with velocity `upsilon` at an angle of `30^(@)` to the horizontal and another body B of the same mass is thrown with velocity `upsilon` at an angle of `60^(@)` to the horizontal, find the ratio of the horizontal range and maximum height of A and B.
View SolutionA ball of mass M is thrown vertically upwards. Another ball of mass 2M is thrown at an angle `theta` with the vertical. Both of them stay in air for the same period of time. The heights attained by the two are in the ratio
View SolutionA skilled gunman always keeps his gun slightly tilted above the line of sight while shooting. Why?
View SolutionIn long jump, does it matter how height you jump ? What factors determine the span of the jump ?
View SolutionA body is thrown horizontally with a velocity `v` from a tower ` H` metre high .After how much time and at what distance from the base of the towrt will the body strike the ground ?
View SolutionA ball is thrown horizontally and at the same time another ball is dropped down from the top of a tower Will both the balls reach the ground at the same time ?
View SolutionA ball is thrown horizontally and at the same time another ball is dropped down from the top of a tower Will both strike the ground with the same velocity ?
View SolutionA horizontal stream of water leaves an opening in the side of a tank. If the opening is h metre above the ground and the stream hits the round D metre away, then what is the speed of water as it leaves the tank in terms of g, h and D ?
View SolutionA railway carriage moves over a straight track with acceleration a. Passenger in the carriage drops a stone. What is the acceleration of the stone w.r.t. the carriage and the earth?
View SolutionA glass marble slides from rest from the topmost point of a vertical circle of radius r along a smooth chord. Does the time of descent depend upon the chord chosen ?
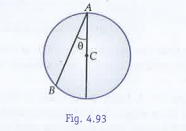
View SolutionThe x and y-components of vector A are 4 m and 6 m respectively. The x and y-components of vector A + B are 10 m and 9 m respectively. Calculate for the vector B the following:
(a) its x and y-components
(b) its length
(c ) the angle it makes with x-axis.
View SolutionThe x and y-components of vector A are 4 m and 6 m respectively. The x and y-components of vector A + B are 10 m and 9 m respectively. Calculate for the vector B the following:
(a) its x and y-components
(b) its length
(c ) the angle it makes with x-axis.
View SolutionThe x and y-components of vector A are 4 m and 6 m respectively. The x and y-components of vector A + B are 10 m and 9 m respectively. Calculate for the vector B the following:
(a) its x and y-components
(b) its length
(c ) the angle it makes with x-axis.
View SolutionA biard is at a point `P(4m,-1m,5m)` and sees two points `P_(1) (-1m,-1m,0m)` and `P_(2)(3m, -1m,-3m)`. At time `t=0`, it starts flying in a plane of the three positions, with a constant speed of `2m//s` in a direction perpendicular to the straight line `P_(1)P_(2)` till it sees `P_(1)` & `P_(2)` collinear at time t. Find the time t.
View SolutionA person travelling eastward with a speed of `3 kmh^(-1)` finds that wind seems to blow from north. On doubling his speed, the wind appears to flow from north-east. Find the magnitude of the actual velocity of the wind.
View SolutionConsider a collection of a large number of particles each with speed v. The direction of velocity is randomly distributed in the collection. Show that the magnitude of the relative velocity between a pair of particles averaged over all the pairs in the collection is greater than v.
View SolutionA ball rolls off the top of a stairway with a constant horizontal velocity u. If the steps are h metre high and w metre wide, show that the ball will just hit the edge of nth step if `n = 2hu^(2)/gw^(2)`
View SolutionShow that the motion of one projectile as seen from another projectile will always be a straight line motion.
View SolutionA boy playing on the roof of a 10 m high building throws a ball with a speed of 10 m/s at an angle ` 30 ^@ ` with the horizontal. How far from the throwing point will the ball be at the height of 10 m from the ground?
` (g = 10 m//s ^ 2 ) `
View SolutionA ball is thrown from a point with a speed 'v^(0)' at an elevation angle of `theta` . From the same point and at the same instant , a person starts running with a constant speed `('v_(0)')/(2) ` to catch the ball . Will the person be able to catch the ball ? If yes, what should be the angle of projection `theta` ?
View SolutionA projectille can have the same range` R` for two angles of projection. If ` t_(1)` and `t_(2)` be the time of flight in the two cases, then find the relation between ` t_(1), t_(2)` and `R` .
View SolutionState, for each of the following physical quantities, if it is a scalar or a vector. Volume, mass speed acceleration, density, number of moles, velocity, angular frequency, displacement, angular velocity.
View SolutionPick out the two scalar quantities in the following list: force, angular momentum, work, current, linear momentum, electric field, average force, angular momentum, work, current , linear momentum, electric field, average velocity, magnetic moment, relative velocity.
View SolutionPick out the only vector quantity in the following list : temperature, pressure, impulse, time, power. Total path-length, energy. Gravitational potential, coefficient of friction, charge,
View SolutionState with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:
(i) Adding any two scalars (ii) Adding a scalar to a vector of the same dimensions
(iii) Multiplying any vector by any scalar (iv) Multiplying any two scalars
(v) Adding any two vectors
View SolutionState with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:
(i) Adding any two scalars (ii) Adding a scalar to a vector of the same dimensions
(iii) Multiplying any vector by any scalar (iv) Multiplying any two scalars
(v) Adding any two vectors
View SolutionState with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:
(i) Adding any two scalars (ii) Adding a scalar to a vector of the same dimensions
(iii) Multiplying any vector by any scalar (iv) Multiplying any two scalars
(v) Adding any two vectors
View SolutionState with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:
(i) Adding any two scalars (ii) Adding a scalar to a vector of the same dimensions
(iii) Multiplying any vector by any scalar (iv) Multiplying any two scalars
(v) Adding any two vectors
View SolutionState with reasons, whether the following algebraic operations with scalar and vector physical quantities are meaningful:
(i) Adding any two scalars (ii) Adding a scalar to a vector of the same dimensions
(iii) Multiplying any vector by any scalar (iv) Multiplying any two scalars
(v) Adding any two vectors
View SolutionRead each statement below carefully and state with reasons, with it is true or false :
(a) The magnitude of vector is always a scalar.
(b) Each component of a vector is always a scalar.
(c ) The total path length is always equal to the magnitude of the displacement vector of a particle.
(d) The average speed of a particle (defined as total path length divided by the time taken to cover the path) is greater or equal to the magnitude of average velocity of the particle over the same interval of time.
(e ) three vectors not lying in a plane can never add up to give a null vector.
View SolutionRead each statement below carefully and state with reasons, with it is true or false :
(a) The magnitude of vector is always a scalar.
(b) Each component of a vector is always a scalar.
(c ) The total path length is always equal to the magnitude of the displacement vector of a particle.
(d) The average speed of a particle (defined as total path length divided by the time taken to cover the path) is greater or equal to the magnitude of average velocity of the particle over the same interval of time.
(e ) three vectors not lying in a plane can never add up to give a null vector.
View SolutionRead each statement below carefully and state with reasons, with it is true or false :
(a) The magnitude of vector is always a scalar.
(b) Each component of a vector is always a scalar.
(c ) The total path length is always equal to the magnitude of the displacement vector of a particle.
(d) The average speed of a particle (defined as total path length divided by the time taken to cover the path) is greater or equal to the magnitude of average velocity of the particle over the same interval of time.
(e ) three vectors not lying in a plane can never add up to give a null vector.
View SolutionRead each statement below carefully and state with reasons, if it is true or false. Three vectors not lying in a plane can never add up to give a null vector.
View SolutionEstablish the following inequalities geometrically or otherwise ,
(a) ` | vec A + vec B| lt= | vec A | + |vec B|` ,
(b) ` | vec A + vec B| gt= ||vec A|- | vec B||`
(C )` | vec A- vec B| lt= | vec A| + |vec B|`
(d) `| vec A- vec B| gt= || vec A| - | vec B||`
When does the equality sign above apply ?
View SolutionEstablish the following vector inequalities geometrically or otherwise: `|vec a+ vec b|ge |vec a| -|vec b|`. When does the equality sign above apply?
View SolutionEstablish the following inequalities geometrically or otherwise ,
(a) ` | vec A + vec B| lt= | vec A | + |vec B|` ,
(b) ` | vec A + vec B| gt= ||vec A|- | vec B||`
(C )` | vec A- vec B| lt= | vec A| + |vec B|`
(d) `| vec A- vec B| gt= || vec A| - | vec B||`
When does the equality sign above apply ?
View SolutionEstablish the following inequalities geometrically or otherwise ,
(a) ` | vec A + vec B| lt= | vec A | + |vec B|` ,
(b) ` | vec A + vec B| gt= ||vec A|- | vec B||`
(C )` | vec A- vec B| lt= | vec A| + |vec B|`
(d) `| vec A- vec B| gt= || vec A| - | vec B||`
When does the equality sign above apply ?
View SolutionGiven ` vec A + vec B+ vec C + vec D =0`, which of the following statements are correct ?
(a) ` vec A, vec B ,vec C ` abd ` vec D` each must be a null vector.
(b) The magnitude of ` ( vec A + vec C)` equals the magnitude of ` ( vec B + vec D)`.
(c ) The magnitude of ` vec A` can never be greater than the sum of the magnitude of ` vec B , vec C ` and `vec D`.
( d) ` vec B + vec C` must lie in the plane of ` vec A + vec D`. if `vec A` and `vec D` are not collinear and in the line of ` vec A` and `vec D`, if they are collinear.
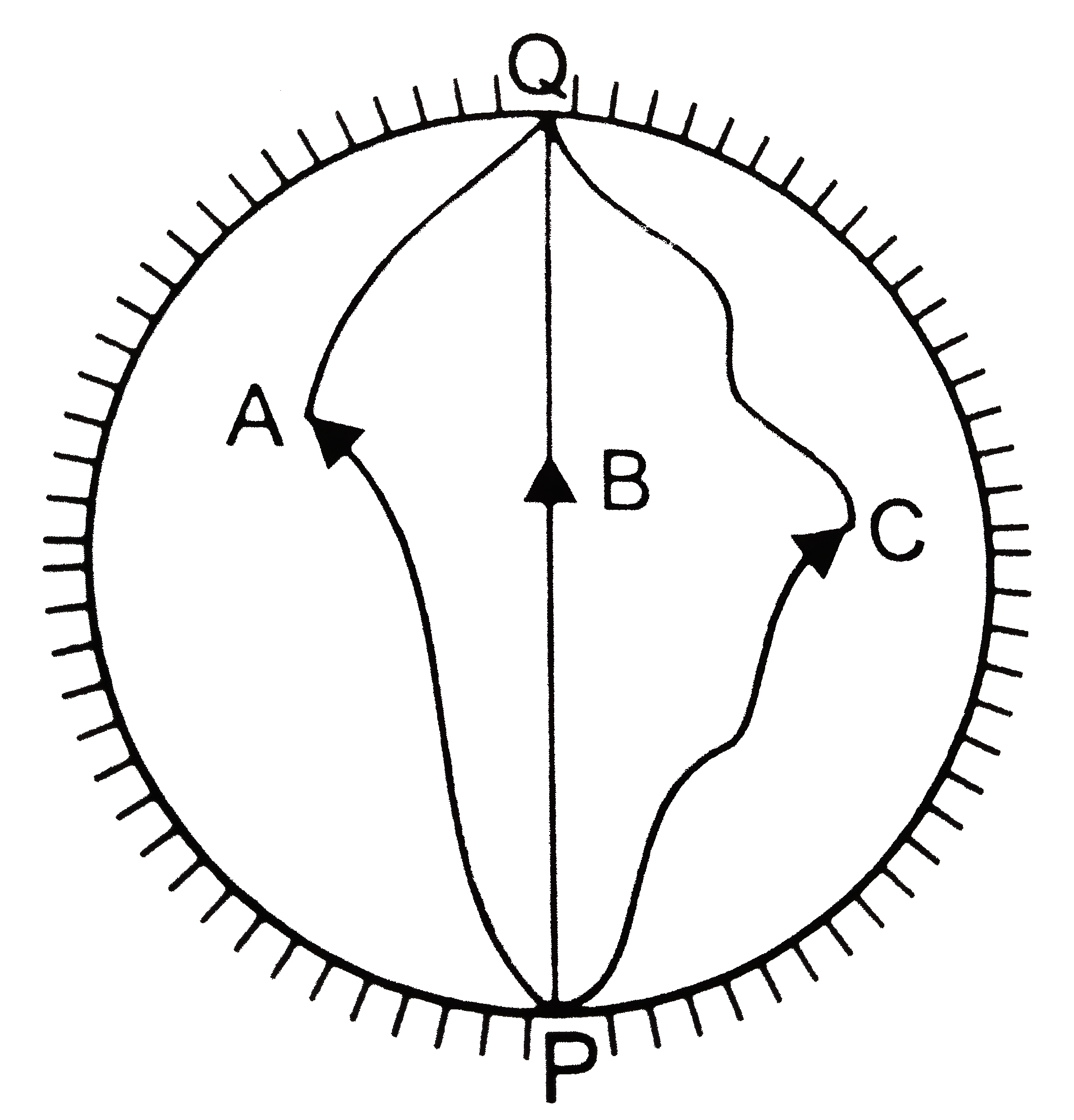
View SolutionThree girls skating on a circular ice ground of radius ` 200 m` start from a point (P) on the edge of the ground and reach a point ` Q` diametrically opposite to (P) following different paths as shown in Fig. (NCT) . 17. What is the magnitude of the displacement vector for each ? which girl's displacement is equal to the actual length of path skated ?
 .
.
View SolutionA cyclist travels from centre O of a circular park of radius 1 km and reaches point P. After cycling along `1//4` th of the circumference along PQ, he returns to the centre of the park along QO. If the total time taken is 10 minutes, calculate (i) net displacement (ii) average velocity and (ii) average speed of the cyclist.
View SolutionA cyclist travels from centre O of a circular park of radius 1 km and reaches point P. After cycling along `1//4` th of the circumference along PQ, he returns to the centre of the park along QO. If the total time taken is 10 minutes, calculate (i) net displacement (ii) average velocity and (ii) average speed of the cyclist.
View SolutionA cyclist travels from centre O of a circular park of radius 1 km and reaches point P. After cycling along `1//4` th of the circumference along PQ, he returns to the centre of the park along QO. If the total time taken is 10 minutes, calculate (i) net displacement (ii) average velocity and (ii) average speed of the cyclist.
View SolutionOn an open ground , a motorist follows a track that turns to his left by an angle of ` 60^@` after every ` 500 m`. Starting from a given turn , specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with total path length covered by the motorist in each case.
View SolutionA passenger arriving in a new town wishes to go from the station to a hotel located ` 10 km` away on a straight road from the station. A dishonest cabman takes him along a circuitous path ` 23 km` long and reaches the hotel in ` 28` minutes . What is (a) the average speed of the taxi, (b) the magnitude of average velocity ? Are the two equal ?
View SolutionA passenger arriving in a new town wishes to go from the station to a hotel located ` 10 km` away on a straight road from the station. A dishonest cabman takes him along a circuitous path ` 23 km` long and reaches the hotel in ` 28` minutes . What is (a) the average speed of the taxi, (b) the magnitude of average velocity ? Are the two equal ?
View SolutionRain is falling vertically with a speed of ` 30 ms^(-1)` . A woman rides a bicycle with a speed of ` 10 ms^(-1)` in the North to South direction. What is the direction in which she should hold her umbrella ?
View SolutionA man can swim with a speed 4km/hr in still water.
(a) How long does he takes to cross a river 1 km wide if the river flows steadily at 3 km/hr and makes his strokes normal to the river current?
(b) How far down the river does he go when he go when he reaches the other bank?
View SolutionIn a harbour, wind is blowing at the speed of ` 72 km //h` and the flag on the mast of a boat anchored in the harbour flutters along the N-E` direction`. If the boat starts moving at a speed of ` 51 km// h` to the North, what is the direction of flag on the mast of the bat ?
View SolutionThe ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of `40 ms^(-1)` can go without hitting the ceiling of the hall ?
View SolutionA cricketer can throw a ball to a maximum horizontal distance of 100 m. How high above the ground can the cricketer throw the same ball ?
View SolutionA stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 seconds, what is the magnitude and direction of acceleration of the stone ?
View SolutionAn aircraft executes a horizontal loop of radius 1 km with a steady speed of `900 km h^(-1)`. Compare its centripetal acceleration with the acceleration due to gravity.
View SolutionRead each statement below carefully and state, with reasons, if it is true or false : The net acceleration of a particle in circular motion is always along the radius of the circle towards the centre.
View SolutionRead each statement below carefully and state, with reasons, if it is true or false : (a) The net acceleration of a particle in circular motion is always along the radius of the circle towards the centre.
(b) The velocity vector of a particle at a point is always aling the tagent to the path of the partile at that point. ltbRgt (c ) The acceleration vector of a particle in uniform circular motion acraged over one cycle is a null vector.
View SolutionRead each statement below carefully and state, with reasons, if it is true or false : The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector.
View SolutionThe position of a particle is given by ` vec r= 3.0 t hat i - 2.0 t^2 hat j + 4.0 hat k m`, wher (t) in seconds and the coefficients have the proper units for ` vec r` to be in metres. (a) Fing the ` vec v` and ` vec a` of the particle ? (b) What is the magnitude and direction fo velocity of the particle at ` t= 2 s`?
View SolutionThe position of a particle is given by ` vec r= 3.0 t hat i - 2.0 t^2 hat j + 4.0 hat k m`, wher (t) in seconds and the coefficients have the proper units for ` vec r` to be in metres. (a) Fing the ` vec v` and ` vec a` of the particle ? (b) What is the magnitude and direction fo velocity of the particle at ` t= 2 s`?
View SolutionA particle starts from the origin at ` t=0` with a velocity of ` 10.0 hat j m//s` and moves in the X-y plane with a constant accleration of ` ( 8.0 hat I + 2. 0 hat j ) ms^(-2)` . (a) At wht time is the x-coordinate of the particle ` 16 m` ? What is the y-coordinate of the particle at that time ? ( b) What is the speed of the particle at that time ?
View SolutionA particle starts from the origin at ` t=0` with a velocity of ` 10.0 hat j m//s` and moves in the X-y plane with a constant accleration of ` ( 8.0 hat I + 2. 0 hat j ) ms^(-2)` . (a) At wht time is the x-coordinate of the particle ` 16 m` ? What is the y-coordinate of the particle at that time ? ( b) What is the speed of the particle at that time ?
View SolutionIf `hati andhatj ` are unit vectors along X- and Y-axis respectively, then what is the magnitude and direction of `hati+hatjandhati-hatj` ?
View SolutionFind the components of vector `vec(a)=3hat(i)+4hat(j)` along the direction of vectors `hat(i)+hat(j)` & `hat(i)-hat(j)`
View SolutionDISPLACEMENT VECTOR
View SolutionA Body moves 6m north, 8m east and 10m vertically upwards, what is its resultant displacement from initial position
View SolutionIf `vec A = vec B+ vec C` and the values of `vec A, vec B and vec C` are 13, 12 and 5 respectively, then the angle between `vec A` and `vec C` will be
View SolutionIf `vec P+ vec Q = vec R` and `|vec P| = |vec Q| = | vec R|`, then angle between `vec P` and `vec Q` is
View SolutionThe square of resultant of two equal forces is three times their product. Angle between the force is
View SolutionLet the angle between two non-zero vectors `vec(A)` and `vec(B)` be `120^(@)` and its resultant be `vec(C)` then:
View SolutionThe three initial and final position of a man on the X-axis are given as
(i) `(-8m, 7m)` (ii) `(7m, -3m)`
(iii) `(-7m, 3m)`
Which pair gives the negative displacement ?
View SolutionA bird flies from (-3 m,4 m,-3 m ) to (7 m, -2 m, -3 m) in XYZ co-ordinates. The bird's displacement in unit vectors is given by
View SolutionIf a unit vector is represented by `0.5 hat(i) + 0.8 hat(j) + c hat(k)` , then the value of `c` is
View SolutionTwo vectors are perpendicular if
View Solution
Excercise questions and complete solutions for chapter Motion in a Plane of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11