Complete Solutions to Example of chapter Motion in a Plane of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | Motion in a Plane |
| SL ARORA | Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Let ABCD is a parallelogram and `vecAC, vecBD` be its diagonal, then `vecAC +vec BD` is
View SolutionLet ABCD is a parallelogram and `vecAC, vecBD` be its diagonal, then `vecAC +vec BD` is
View SolutionA body is simultaneously given two velocities : one ` 12 ms^(-1)` due East and other ` 5 ms^(-1)` due North. Find the resultant velocity.
View SolutionA particle has a displacement of 12 m towards east and 5m towards the north and then 6m vertically upward. Find the magnitude of the sum of these displacements.
View SolutionTwo forces of 5N and 7N act on a a particle with an angle of `60^(@)` between them. Find the resultant force.
View SolutionTwo vectors, both equal in magnitude, have their resultant equal in magnitude of the either. Find the angle between the two vectors.
View SolutionTwo equal forces have their resultant equal to either. At what angle are they inclined ?
View SolutionTwo forces whose magnitudes are in the ratio `3:5` give a resultant of 28N. If the angle of their inclination is `60^@`, find the magnitude of each force.
View SolutionTwo forces equal to P and 2P newton act on a particle. If the first be doubled and the second be increased by 20 newton, the direction of the resultant is unaltered. Find the value of P.
View SolutionThe greatest and the least resultant of two force acting at a point are 29N and 5N respectively. If each force is increased by 3N, find the resultant of two new forces acting at right angle of each other.
View SolutionThe sum of the magnitudes of two forces acting at a point is 18 and the magnitude of their resultant is 12. If the resultant is at `90^(@)` with the force of smaller magnitude, What are the magnitudes of forces?
View SolutionA motor boat is racing towards North at `25 km//h` and the water current in that region is `10 km//h` in the direction of `60 ^(00` East of South. Find the resultant velocity of the boat.
View SolutionOn a certain day, rain was falling vertically with a speed of `35ms^(-1)` . A wind started blowing after sometime with a speed of `12ms^(-1)` in east to west direction . In which direction should boy waiting at a bus stop hold his umbrella ?
View SolutionA river 800 m wide flows at the rate of `5kmh^(-1)`. A swimmer who can swim at `10 kmh^(-1)` in still water, wishes to cross the river straight. (i) Along what direction must be strike ? (ii) What should be his resultant velocity ? (iii) How much time he would take ?
View SolutionA river 800 m wide flows at the rate of `5kmh^(-1)`. A swimmer who can swim at `10 kmh^(-1)` in still water, wishes to cross the river straight. (i) Along what direction must be strike ? (ii) What should be his resultant velocity ? (iii) How much time he would take ?
View SolutionA river 800 m wide flows at the rate of `5kmh^(-1)`. A swimmer who can swim at `10 kmh^(-1)` in still water, wishes to cross the river straight. (i) Along what direction must be strike ? (ii) What should be his resultant velocity ? (iii) How much time he would take ?
View SolutionA boat man can row with a speed of ` 10 km h^(-1)` in still water. If the river flows steadily at ` 5 km //h`, in which direction should the boatman row in order to reach a point on the other bank directly opposite to the point from where he stared ? The width of the river is ` 2 km`.
View SolutionA car travelling a `20 ms^(-1)` due north along the highway makes a right turn on to a side road that heads due east. It takes 50s for the car to complete the turn. At the end of 50 second, the car has a speed of `15 ms^(-1)` along the side road. Determine the magnitude of average acceleration over the 50 second interval.
View SolutionFind the vector `vec(AB)` and its magnitude if it has initial point A(1,2,-1) and final point B(3,2,2).
View SolutionFind unit vector parallel to the resultant of the vectors `vec(A) = hati +4hatj +2hatk` and `vec(B) = 3hati - 5hatj +hatk`.
View SolutionA vector `vec(X)`, when added to the resultant of the vectors `vec(A) = 3hati - 5hatj +7hatk` and `vec(B) = 2hati +4hatj - 3hatk` gives a unit vector along Y-axis. Find the vector `vec(X)`.
View SolutionTwo forces `vec(F)_(1) = 3hati +4hatj` and `vec(F)_(2) = 3hatj +4hatk` are acting simultaneously at a point. What is the magnitude of the resultant force ?
View SolutionIf `vec(A) = 3hati +4hatj` and `vec(B) = 7 hat I +24 hatj`, find a vector having the same magnitude as `vec(B)` and parallel to `vec(A)`.
View SolutionA bird moves with velocity 20m/s in a direction making an angle of `60^(@)` with the eastern line and `60^(@)` with the vertical upward. Represent the velocity vector in rectangular form.
View SolutionOne of the rectangular components of a velocity of `80 kmh^(-1)` is `40 kmh^(-1)`. Find the other component.
View SolutionA force is inclined at `60^(@)` to the horizontal. If its rectangular component in the horizontal direction be 50N,find the magnitude of the force and its vertical component.
View SolutionAn aeroplane takes off at angle of `30^(@)` to the horizontal. If the component of its velocity along the horizontal is `250 kmh^(-1)`, what is the actual velocity ? Find also the vertical component of the velocity.
View SolutionA man rows a boat with a speed of `18Km h^(-1)` in the north-west direction (figure). The shoreline makes an angle of `15^(@)` south of west. Obtain the components of the velocity of the boat along the shoreline and perpendicular to the shoreline.

View SolutionTwo billiard balls are rolling on a flat table. One has the velocity components `v_(x) = 1 ms^(-1), v_(y) = sqrt(3)ms^(-1)` and the other has components `v'_(x) = 2ms^(-1)` and `v'_(y) = 2ms^(-1)`. If both the balls start moving from the same point, what is the angle between their paths ?
View SolutionFind the angle between the vertors `vec(A) = hati + 2hatj - hatk` and `vec(B) = - hati +hatj - 2hatk`.
View SolutionProve that the vectors `vec(A) = hati +2 hatj +3hatk` and `vec(B) = 2hati - hatj` are perpendicular to each other.
View SolutionTwo vector `vec A = 5hati+7hatj-3hatk and vec B=2hati+2hatj-alphahatk` are mutually perpendicular to each other. What is the value of `alpha` ?
View SolutionIf the magnitudes of two vectors are 3 and 4 and their scalar product is 6, then find the angle between the two vectors.
View SolutionA body constrained to move along the z-axis of a co-ordinate system is subjected to a constant force `vec(F)` given by `vec(F) =- hati +2hatj +3hatk` newton, where `hati, hatj` and `hatk` represen unit vectors along x,y- and z-axis of the system respectively. Calculate the work done by force in displacing the body through a distance of 4m along the z-axis.
View SolutionA force of `7 hati+ 6 hatk` newton makes a body move on a rough plane with a velocity of `3 hatj + 4 hatk` `ms^-1` . Calculate the power in watt.
View SolutionThree vectors `vec(A),vec(B)` and `vec(C)` are such that `vec(A) = vec(B)+vec(C)` and their magnitude are 5,4 and 3 respectively. Find the angle between `vec(A)` and `vec(C)`.
View SolutionIf `|vec A + vec B|=|vec A-vecB|`, finf the angle between `vec A and vec B`.
View SolutionIf vector `P, Q and R` have magnitude 5,12,and 13 units and `vec(P)+vec(Q)=vec(R )`, the angle between Q and R is
View SolutionDetermine the angles which the vector
`vec(A) = 5 hati + 0 hatj +5hatk` makes with X-,Y- ad Z-axes.
View SolutionIf unit vectors `hat(a)` and `hat(b)` are inclined at angle `theta`, then prove that
`|vec(a) - vec(b)| = 2 sin.(theta)/(2)`.
View SolutionIf `vec(A) +vec(B) = vec(C)` and `A^(2) +B^(2) = C^(2)`, then prove that `vec(A)` and `vec(B)` are perpendicular to each other.
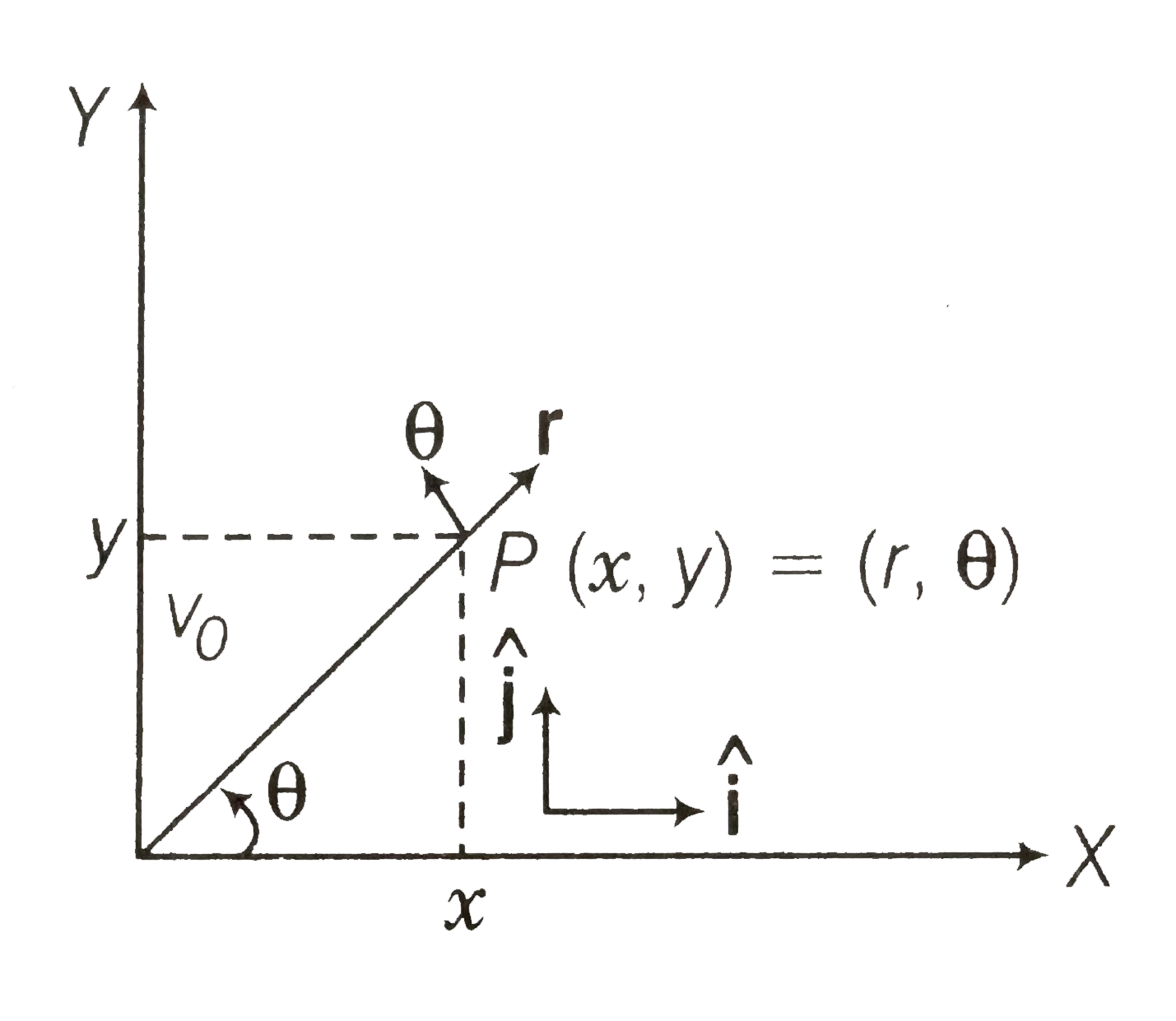
View SolutionMotion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian coordinates `A=A_(x)hat(i) + A_(y)hat(j)`, where `hat(i)` and `hat(j)` are unit vector along x and y-directions, respectively and `A_(x)` and `A_(y)` are corresponding components of A. Motion can also be studied by expressing vectors in circular polar coordinates as `A= A_(r)hat(r) + A_(theta) hat(theta)`, where `hat(r)=(r)/(r)=cos theta hat(i)+sin theta hat (j)` and `hat(theta)=-sin theta hat(i) + cos theta hat (j)` are unit vectors along direction in which r and `theta` are increasing.
(a) Express `hat(i)` and `hat (j) ` in terms of `hat(r) ` and `hat (theta)`.
(b) Show that both `hat(r)` and `hat(theta)` are unit vectors and are perpendicular to each other.
(c) Show that `(d)/(dt)(hat(r))= omega hat(theta)`, where `omega=(d theta)/(dt)` and `(d)/(dt) (hat(theta))=-thetahat(r)`.
(d) For a particle moving along a spiral given by `r=a theta hat(r)`, where a = 1 (unit), find dimensions of a .
(e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
View SolutionProve that the vectors `vec(A) = 2hati - 3hatj - hatk` and `vec(B) =- 6 hati + 9hatj +3hatk` are parallel.
View SolutionCalculate the area of a paralleleogram whose two adjacent sides are formed by the vectors
` vec A =3 hat I + 5 hat j and vec B =- 3 hat I + 7 hat j`.
View SolutionIf `vec(A)` and `vec(B)` denpte the sides of a parallelogram and its area is `AB//2`, find the angle between `vec(A)` and `vec(B)`.
View SolutionThe unit vector perpendicular to `vec A = 2 hat i + 3 hat j + hat k` and ` vec B = hat i - hat j + hat k` is
View SolutionFind a unit vector perpendicular to each one of the vectors `vec(a) = 4 hat(i) - hat (j) + 3hat(k)` and `vec(b) = 3 hat(i) + 2 hat(j) - hat(k)`.
View SolutionDetermine the sine of the angle between the vectors ( `3 hat i+ 3hat j+ 4 hat k`) and ( `3 hat i-2 hat j - 4 hat k)`.
View SolutionShow that `(vec(A) - vec(B)) xx (vec(A) +vec(B)) = 2(vec(A) xx vec(B))`
View SolutionFor any three vectors `vec(A), vec(B)` and `vec(C)` prove that
`vec(A) xx (vec(B) +vec(C)) +vec(B) xx (vec(C) +vec(A)) + vec(C) xx (vec(A) +vec(B)) = vec(O)`
View SolutionFor any to vectors ` vec A and vec B`, prove that
`| vec A xx vec B|^2 = A^2 B^2 - ( vec A. vec B)^2`.
View SolutionFind `vec(A).vec(B)` if `|vec(A)| = 2, |vec(B)| = 5` and `|vec(A) xx vec(B)| =8`
View SolutionFind the area of the rriangle formed by the tips of the vectors,
` vec a= (2 hat I - hat j+ 3 hat k), vec b= 4 hat I + 3 hat j-hat k`,
` vec C= 3 hat I - hat j + 2 hat k`.
View SolutionFind the magnitude and direction cosines of the torque about the point `(3, 1, -2)` of a force ` 3 hat i + 2 hat j + hat k ` whose line of action passes through that ` (1, 2, -1) `
View SolutionFind the area of parallelogram whose diagonals are the vectors `3 hat i + hat j - hat k` and `hat i - 3 hat j + 4 hat k.`
View SolutionIn any `triangle ABC`, prove that `a sin A-b sin B -=c sin (A-B)`.
View SolutionIf ` vec a ,\ vec b ,\ vec c` are three vectors such that ` vec adot\ vec b= vec adot\ vec c` and ` vec a\ x\ vec b= vec a\ x\ vec c ,\ vec a\ !=0` , then show that ` vec b= vec c` .
View SolutionIf `vec A=hat i + 2 hat j -3 hat k`,
`vec B =2 hat I -hat j + hat k` and ` vec C= hat i -3 hat j + 2 hat k`, then find ` vec A xx ( vec B xx vec C)`.
View SolutionA cyclist moves along a circular path of radius 70 m. If he completes one round in 11 s, calculate (i) total length of path, (ii) magnitude of the displacement, (iii) average speed, and (iv) magnitude of average velocity.
View SolutionA cyclist moves along a circular path of radius 70 m. If he completes one round in 11 s, calculate (i) total length of path, (ii) magnitude of the displacement, (iii) average speed, and (iv) magnitude of average velocity.
View SolutionA cyclist moves along a circular path of radius 70 m. If he completes one round in 11 s, calculate (i) total length of path, (ii) magnitude of the displacement, (iii) average speed, and (iv) magnitude of average velocity.
View SolutionA cyclist moves along a circular path of radius 70 m. If he completes one round in 11 s, calculate (i) total length of path, (ii) magnitude of the displacement, (iii) average speed, and (iv) magnitude of average velocity.
View SolutionA particle is moving eastwards with a velocity of ` 5 ms_(-1)`. In `10 seconds` the velocity changes to `5 ms^(-1)` northwards. The average acceleration in this time is
View SolutionThe position of a particle is given by
`r = 3t hati +2t^(2) hatj +8 hatk`
where, t is in seconds and the coefficients have the proper units for r to be in metres.
(i) Find v (t) and a(t) of the particles.
(ii) Find the magnitude and direction of v(t) and a(t) at `1 = 1s`.
View SolutionThe position of of a particle is given by `vec r =3.0 t hat I + 2.0 t^(2) hat j+ 5.0 hat k` wher (t) in seconds and the coefficients mave the proper units for `ve r` to ber in metres. Find the velocity and acceleration of the particle in magnitude and direction at time `t=3.0 s`
View SolutionIf the position vector of a particle is given by `vec r =(94 cos 2t) hat i + (4 sin 2t) hat j + (6t) hat km`, calculate its acceleration at `t=pi//4 second `.
View SolutionA boat is moving with a velocity `(3hati +hatj)` with respect to ground. The water in the river is moving with a velocity `-3hati - 4hatj` with respect to ground. What is the relative velocity of boat with respect to river ?
View SolutionA particle P is moving along a straight line with a velocity of `3ms^(-1)` and another particle Q has a velocity of `4ms^(-1)` at an angle of `30^(@)` to the path of P. Find the speed of Q relative to P.
View SolutionTo a driver going east in a car with a velocity of `40 km h^(-1)`, a bus appears to move towards north with a velocity of `40 sqrt(3)km h^(-1)`. What is the actual velocity and direction of motion of the bus ?
View SolutionA man directly crosses a river in time `t_1` and swims down the current a distance equal to the width of the river I time `t_2`. If `u and v` be the speed of the current and the man respectively, show that `t_1`: `t_2`: : `sqrt(v + u)` : `sqrt(v - u))`.
View SolutionA hiker stands on the edge of a cliff `490 m` above the ground and throwns a stone horiozontally with an initial speed of `15ms^(-1)` neglecting air resistance.The time taken by the stone to reach the ground in seconds is `(g=9.8ms^(2))`
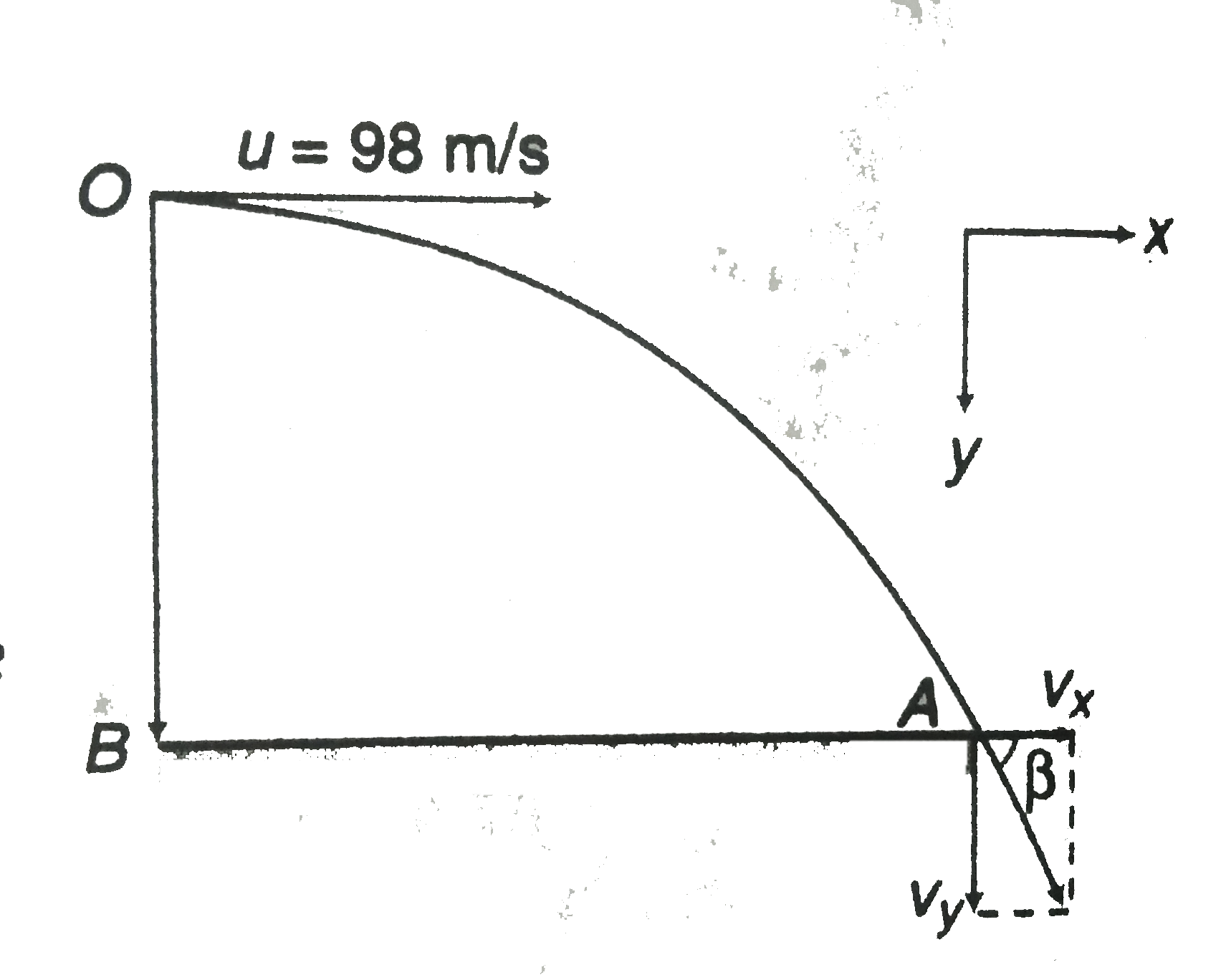
View SolutionA projectile is fired horizontally with a velocity of `98 ms^(-1)` from the top of a hill 490 m high. Find (i) the time taken to reach the ground (ii) the distance of the target from the hill and (iii) the velocity with which the projectile hits the ground.
View SolutionA projectile is fired horizontally with a velocity of `98 ms^(-1)` from the top of a hill 490 m high. Find (i) the time taken to reach the ground (ii) the distance of the target from the hill and (iii) the velocity with which the projectile hits the ground.
View SolutionA projectile is fired horizontally with velocity of 98 m/s from the top of a hill 490 m high. Find
(a) the time taken by the projectile to reach the ground,
(b) the distance of the point where the particle hits the ground from foot of the hill and
(c) the velocity with which the projectile hits the ground. `(g= 9.8 m//s^2)`
 .
.
View SolutionA body is thrown horizontally from the top of a tower and strikes the ground after three seconds at an angle of `45^@` with the horizontal. Find the height of the tower and the speed with which the body was projected. (Take ` g = 9.8 m//s^2`)
View SolutionA bomb is dropped from an aeroplane when it is directly above a target at a height of 1000m. The aeroplane is moving horizontally with a speed of `500 kmh^(-1)`. By how much distance will the bomb miss the target ?
View SolutionA body is projected horizontally from the top of a cliff with a velocity of `9.8ms^(-1)`. What time elapes before horizontal and vertical velocities become equal ? Take `g=9.8 ms^(-2)`.
View SolutionA marksman wishes to hit a target just in the same level as the line of sight. How high from the target he should aim, if the distance of the target is 1600 m and the muzzle velocity of the gun is `800 ms^(-1)` ? Take `g = 9.8 ms^(-2)`.
View SolutionTwo tall buildings face each other and are at a distance of 180 m from each other. With what velocity must a ball be thrown horizontally from a window 55 m above the ground in one building, so that it enters a window 10.9 m above the ground in the second building ?
View SolutionA particle is projected horizontally with a speed `u` from the top of plane inclined at an angle `theta` with the horizontal. How far from the point of projection will the particle strike the plane ?

View SolutionA helicopter on a flood relief mission flying horizontally with a speed u at a altitude h, has to drop a food packet for a victim standing on the ground. At what distance from the victim should the food packet be dropped ?
View SolutionA cricket ball is thrown at a speed of ` 28 ms^(-1)` in a direction `30 ^(@)` above the horizontal. Calculate (a)the maximum height (b) the time taken by ball to return ti the same level, and (c )the distance from the thrower to the point wher the ball restance from the throwrt to the point where the ball returns to the same level.
View SolutionA cricket ball is thrown at a speed of `28 ms^(-1)` in a direction `30^(@)` above the horizontal. Calculate the time taken by the ball to return to the same level.
View SolutionA cricket ball is thrown at a speed of `56 ms^(-1)` in a direction, making an angle `30^@` with the horizontal, Calculate.
the distance from thrower to the point where the ball returns to the earth.
View SolutionA body is projected with a velocity of `30 ms^(-1)` at an angle of `30^(@)` with the vertical. Find the maximum height, time of flight and the horizontal range.
View SolutionA projectile has a range of 50 m and reaches a maximum height of 10 m. Calculate the angle at which the projectile is fired.
View SolutionA boy stands at 39.2 m from a building and throws a ball which just passes through a window 19.6 m above the ground. Calculate the velocity of projection of the ball.
View SolutionFind the angle of projection for which the horizontal range and the maximum height are equal.
View SolutionProve that the maximum horizontal range is four times the maximum height attained by the projectile, when fired at an inclination so as to have maximum horizontal range.
View SolutionA ball is kicked at an angle of `30^(@)` with the vertical. If the horizontal component of its velocity is `19.6 ms^(-1)`, find the maximum height and horizontal range.
View SolutionShow that a given gun will shoot three times as high when elevated at an angle of `60^(@)` as when fired at angle of `30^(@)` but will carry the same distance on a horizontal plane.
View SolutionA ball is thrown at angle `theta` and another ball is thrown at an angle `(90^(@)-theta)` with the horizontal direction from the same point with velocity `39.2 ms^(-1)`. The second ball reaches 50 m higher than the first ball. Find their individual heights. Take `g = 9.8 ms^(-2)`.
View SolutionIf `R` is the horizontal range for `theta` inclination and `h` is the maximum height reached by the projectile, Then maximum range is
View SolutionThere are two angles of projection for which the horizontal range is the same. Show that the sum of the maximum heights for these two angles is independent of the angle of projection.
View SolutionShow that there are two values of time for which is projectile is at the same height. Also show that the sum of these two times is equal to the time of flight.
View SolutionTwo projectiles are thrown with different velocities and at different angles so as to cover the same maximum height. Show that the sum of the times taken by each to reach the highest point is equal to the total time taken by either of the projectiles.
View SolutionA hunter aims his fun and fires a bullet directly at a monkey on a tree. At the instant the bullet leaves the gun, the monkey drops. The bullet
View SolutionA machine gun is mounted on the top of a tower of height `h`. At what angle should the gun be inclined to cover a maximum range of firing on the ground below ? The muzzle speed of bullet is `150 ms^-1`. Take `g = 10 ms^-2`.
View SolutionAt what angle should a body be projected with a velocity `24 ms^(-1)`. Just to pass over the obstacle 16 m high at a horizontal distance of 32 m ? Take `g = 10 ms^(-2)`.
View SolutionA target is fixed on the top of a pole 13 metre high. A person standing at a distance of 50 metre form the pole is capable of projecting a stone with a velocity `10 sqrt(g) ms^(-1)`. If he wants to strike the target in shortest possible time, at what angle should he project the stone ?
View Solution
Example questions and complete solutions for chapter Motion in a Plane of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11