Complete Solutions to Example of chapter Laws of Motion of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | Laws of Motion |
| SL ARORA | Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
(a) Define the term 'force'.
(b) State the various effects of force.
View SolutionWhat were the views of Grek philosphere Aristotle as regard to maintain the state of uniform motion of objects?
View SolutionDescribe Galileo's experiments concerning motionof objects on inclined planes. Hence state the law of inertia.
View Solutiondefine the term inertia. What are the different types of inertia? Give one example of each type.
View SolutionWhat is force ? What is inertia ? How is inertia measured ?
View SolutionTaking suitable examples, develop the concept of momentum.
View SolutionDefine momentum. Is it a scalar or a vector quantity? Give its units and dimensions?
View SolutionState `Newton's three law of motion.
View SolutionState and explain Newton's first law of motion.
View SolutionHow does Newton's first law of motion lead to the definition of force?
View SolutionWhy is Newton's first law of motion also called law of inertia?
View SolutionGive some examples from daily life that illustrate the law of inertia.
View SolutionDescribe the important observation which led Newton to postulate his second law of motion.
View SolutionState and explain Newton's second law of motion.
View SolutionExplain how does Newton's second law of motion give a quantitative definition of force.
View SolutionIs force a scalar or vector quantity? Write its dimensional formula.
View SolutionName and define the various absolute unit gravitational units of force.
View SolutionFind the number of dynes in one newton.
View SolutionConvert Newton into dyne.
View SolutionExpress Newton's second law of motion in component form. Give its significance.
View SolutionGive atleast four applications of Newton's second law of motion.
View SolutionHow does Newton's second law of motion lead to the concept of inertial mass?
View SolutionBriefly explain how an unknown force can be measured with the help of a coiled spring.
View SolutionAn army vehicle of mass 1000 kg is moving with a velocity of `10 m//s` and is acted upon by a forward force of 1000 N due to the engine and a retarding force of 500 N due to friction. What will be its velocity after 10 s
View SolutionA bullet of mass 0.04 kg moving with a speed of `90 ms^(-1)` enters a heavy wooden block and is stooped after a distance of 60 cm . What is the average resistive force exerted by the block on the bullet ?
View SolutionA force of 72 dyne is inclined to the horizontal at an angle of `60^(@)`. Find the acceleration in a mass of 9 g, which moves in a horizontal direction.
View SolutionA sooterist moving with a speed of `36kmh^(-1)` sees a child standing in the middle of the road. He applies the brakes and brings the scooter to rest in 5 s just in time to save child. Calculate the average retarding force on the vehicle, if mass of the vehicle and driver is 300 kg.
View SolutionA bus starts from rest accelerating unifromly with `4 ms^(-2)` . At `t = 10 s` ,a stone is dropped from the window of the bus 2 m high . If `g = 10 m//s^(2)` , what are the magnitude of velocity and acceleration of the stone at 10 .2 s ?
View SolutionA car starts from rest and accelerates uniformly with 2 `ms^(-2)`. At t = 10 s, a stone is dropped out of the window 1 m high of the car. What are the (i) velocity, and (ii) acceleration of the stone at t = `10.1` s? (Neglect air resistance). Take g = `9.8ms^(-2)`.
View SolutionForces of `5sqrt2` and `6sqrt2N` are acting on a body of mass 1000 kg at an angle of `60^(@)` to each other. Find the acceleration, distance covered and the velocity of the mass after 10 s.
View SolutionA block of metal weighing 2kg is resting on a frictionless plane. It is struck by a jet releasing water at a rate of 1kg/s and at a speed of 5 m/s. Calculate the initial acceleration of the block.
View SolutionWhat are impulsive forces? Give examples.
View SolutionShow that the impulse of a force is equal to the change in momentum produced by the force.
View SolutionGive some practical examples from daily life which make use of the conecpt of impulse.
View SolutionA batsman hits back a ball straight in the direction of the bowler without changing its initial speed of `12 ms^(-1)` . If the mass of the ball is 0.15 kg , determine the impulse imparted to the ball . (Assume linear motion of the ball).
View SolutionA cricket ball of mass 150 g moving with a velocity of 15 `ms^(-1)` is brought to rest by a player in `0.05` s. Calculate the impulse and the average force exerted by the player.
View SolutionA rubber ball of mass 50 g falls from a height of 1 m and rebounds to a height of 0.5 m. Find the impulse and the average force between the ball and the ground if the time for which they are in contact was 0.1 s.
View SolutionWhile launcing a rocket of mass `2 xx10^(4)` kg, a force of `5 xx10^(5)` N is applied for 20 s. Calculate the velocity attained by the rocket at the end of 20 s.
View SolutionA machine gun fires a bullet of mass 40 g with a velocity `1200 ms^-1`. The man holding it can exert a maximum force of 144 N on the gun. How many bullets can be fire per second at the most?
View SolutionA ball moving with a momentum of `5 kg ms^(-1)` strikes against a wall at an angle of `45^@` and is reflected at the same angle. Calculate the change in momentum.
View SolutionThe initial speed of a body of mass `2kg` is `5ms^(-1)` A force acts for `4` seconds in the direction of motion of the body. The force time graph is shown in Calculate impulse of the force and also find the speed of the body .
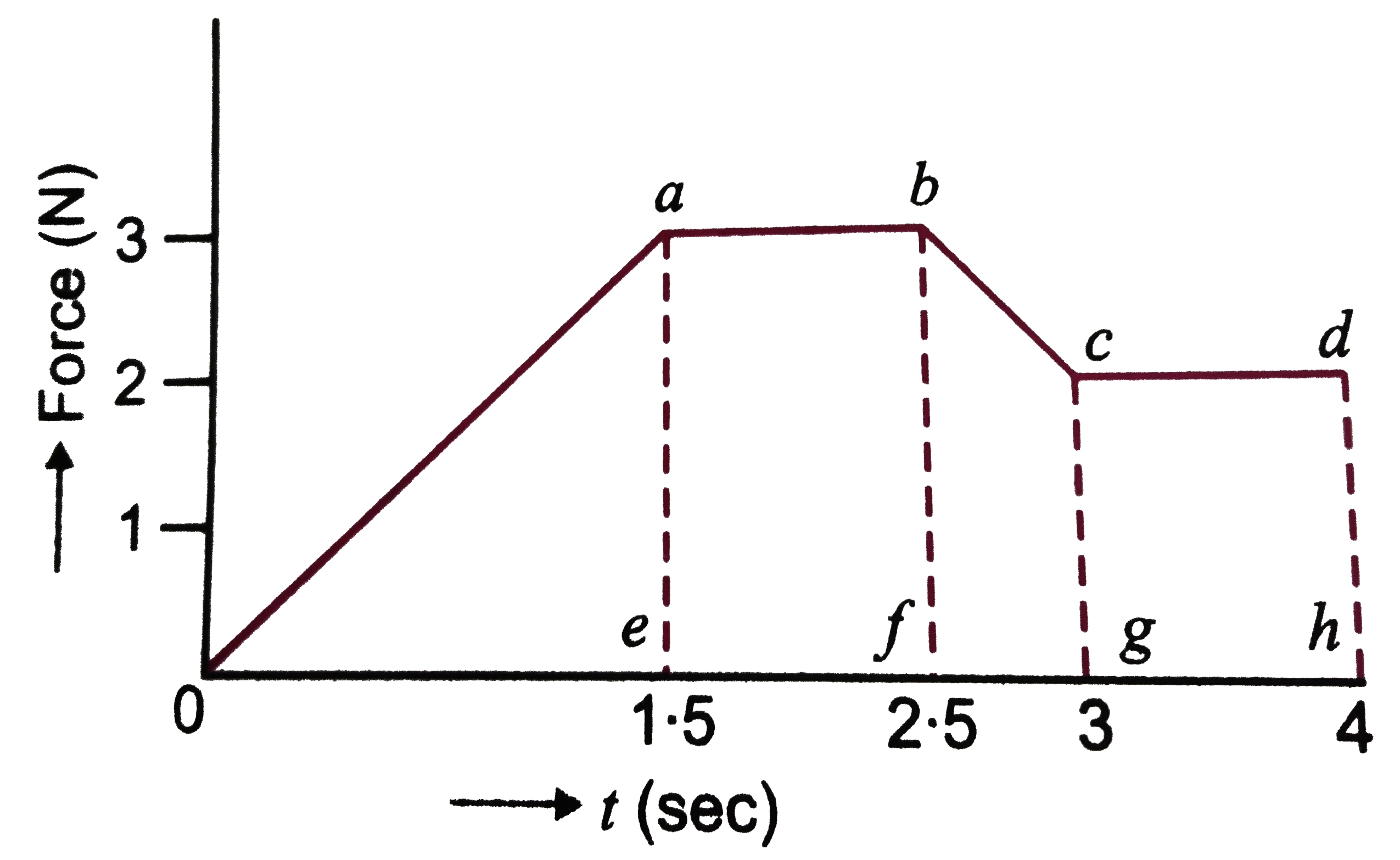 .
.
View SolutionState and explain Newton's third law of motion. How will you prove it experimentally?
View SolutionExplain briefly any three applications of Newton's third law of motion.
View SolutionGive some examples from daily life which illustrate the use of Newton's law of motion.
View SolutionIf action is always equal to the reaction, explain how a horse can pull a cart.
View SolutionShow that Newton's second law of motion is the real law of motion.
View SolutionA man of mass m is standing on the floor of a lift. Find his apparent weight when the lift is moving upwards with uniform acceleration a.
View SolutionA man of mass m is standing on the floor of a lift. Find his apparent weight when the lift is moving downwards with uniform acceleration a.
View SolutionA man of mass m is standing on the floor of a lift. Find his apparent weight when the lift at rest or moving with uniform velocity v.
View SolutionA man of mass m is standing on the floor of a lift. Find his apparent weight when the lift falling freely. Take acceleration due to gravity equal to g.
View SolutionTwo identical billiard balls striks a rigid wall with the same speed but at different angles , and get reflected without any change in speed , as shown in Fig . What is (i) the direction of the force on the wall due to each ball ? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ?
View SolutionTwo identical billiard balls striks a rigid wall with the same speed but at different angles , and get reflected without any change in speed , as shown in Fig . What is (i) the direction of the force on the wall due to each ball ? (ii) the ratio of the magnitudes of impulses imparted to the balls by the wall ?
View SolutionAn elevator weighs `4000kg` When the upward tension in the supporting cable is `48000 N` what is the upward acceleration? Starting from rest, how far does it rise in `3` seconds ?
View SolutionA lift of mass 2000 kg is supported by thick steel ropes . If maximum upward acceleration of the lift be `1.2 m//s^(2)` , and the breaking stress for the ropes be
`2.8 xx 10^(8) Nm^(-2)`
what should be the minimum diameter of rope ?
View SolutionState the law of conservation of linear momentum and describe it from Newton's second law of motion.
View SolutionState the law of conservation of linear momentium. How do you obtain this law from newton's third law ?
View SolutionDerive Newton's third law of motion from the law of conservation of momentum.]
View SolutionGive some examples from daily life which illustrate the law of conservation of linear momentum.
View SolutionA 30 kg shell is flying at 48 `ms^(-1)`. When it explodes, its one part of 18 kg stops, while the remaining part flies on. Find the velocity of the later.
View SolutionA neutron having a mass of `1.67 xx 10^(-27) kg` and moving at `10^(8) m//s`collides with a deuteron at rest and sticks to it. If the mass of the deuteron is `3.33 xx 10^(-27) kg` then the speed of the combination is
View SolutionA car of mass one metric ton travelling at `32m//s`c dashes into the rear of a truck of mass `8000kg` moving in the same direction with a velocity of `4m//s` After the collision the car bounces back wards with a velocity of `8m//s` What is the velocity of the truck after the impact ?
View SolutionA hunter has a machine gun that can fire 50 g bullets with a velocity of `150 m//s` . A 60 kg tiger springs at him with a velocity of `10 ms^(-1)` How many bullets must the hunter fire per secoud into the tiger in order to stop him in his track.
View SolutionA body of mass 1 kg initially at rest explodes and breaks into three fragments of masses in the ratio 1: 1: 3. The two pieces of equal mass fly off perpendicular to each other with a speed of `30 ms^(-1)` each. What is velocity of the heavier fragment?
View SolutionA dise of mass 10 g is kept floating horizontally by throwing 10 marbles per secound against it from below . If mass of each marble is 5 g Calculate the velocity with which marbles are striking the disc . Assume that marbles strike the disc . Normally and rebound downwards with the same speed.
View SolutionWhat is meant by burnt out speed of a rocket?
View SolutionFuel is consumed at the rate of `100 kg s^(-1)` in a rocket. The exhaust gases are ejected at speed of `4.5 xx 10^(4) ms^(-1)`. What is thrust experienced by the rocket?
View SolutionA rocket of initial mass `6000kg` ejects mass at a constant rate of `16kg//s` with constant relative speed of `11m//s` What is the acceleration of the rocket one mnute after blast ?
View SolutionThe mass of a rocket is 500 kg and the relative velocity of the gases ejecting from it is 250 m/s with respect to the rocket. The rate of burning of the fuel in order to give the rocket an initial acceleration `20 m//s^(2)` in the vertically upward direction `g = 10 m/s^(2)`, will be -
View SolutionA rocket is set for vertical firing If the exhaust speed is `1200ms^(-1)` , how much gas must be ejected per second to supply the thrust needed (i) to overcome the weight of rocket (ii) to give to the rocket an initial vertical upward acceleration of `29.6 m//s^(2)` Given mass of rocket = 6000 kg.
View SolutionA rocket is set for vertical firing If the exhaust speed is `1200ms^(-1)` , how much gas must be ejected per second to supply the thrust needed (i) to overcome the weight of rocket (ii) to give to the rocket an initial vertical upward acceleration of `29.6 m//s^(2)` Given mass of rocket = 6000 kg.
View SolutionIf the maximum possible exhaust velocity of a rocket be `2km//s` calculate the ratio `m_(0)//m` for it to acquire a veocity of `11.2km//s` after starting from rest .
View SolutionA rocket motor consumes 100 kg of fuel per second, exhausting it with a speed of `5xx10^(3)ms^(-1)`. (i) What force is exerted on the rocket ? (ii) What will be the velocity of the rocket at the instant its mass is reduced `(1//20)`th of its initial mass, its initial velocity being zero. Neglect gravity.
View SolutionA rocket motor consumes 100 kg of fuel per second, exhausting it with a speed of `5xx10^(3)ms^(-1)`. (i) What force is exerted on the rocket ? (ii) What will be the velocity of the rocket at the instant its mass is reduced `(1//20)`th of its initial mass, its initial velocity being zero. Neglect gravity.
View SolutionWhat do you understand by concurrent forces ? State the conditions for the equilibrium of a particle under the effect of concurrent forces .
View SolutionA mass of 6kg is suspended by a rope of length 2m from a celling a force of 50N in the horizontal direction is applied at the midpoint of the rope as shown in the figure what is the angle the rope makes with the vertical is equalibrium take `g=10 ms^(-2)` neglect mass of the rope

View SolutionDetermine the Tension `T_1` and `T_2` in the srings in Fig. 5.30 (a).
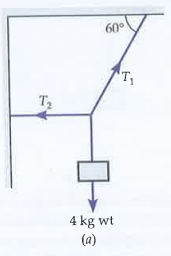
View SolutionA train is moving along a horizontal track . A pendulum suspended from the roof makes an angle of `4^(@)` with the vertical . If `g = 10 m//s^(2)` , what is the acceleration of the train ?
View SolutionA ball of mass `1 kg` hangs in equilibrium from two strings `OA` and `OB` as show in figure. What are the tensions in strings `OA` and `OB`? `(Take g= 10 m//s^(2))`

View SolutionA body of mass m is suspended by two strings making angles `alpha and beta` with the horizontal. Find the tensions in the strings.
View SolutionA uniform rope of length L , resting on frictionless horizontal table is pulled at one end by a force F . What is the tension in the rope at a distance x from the end where the force is applied ?
[ Hint : Consider the motion of the entire rope and the motion of x length of rope using P = ma formula and third law of motion ]
View SolutionWhat is meant by a free-body diagram? What is its use?
View SolutionA pull of 15 N is applied to a rope attached to a block of mass 7 kg lying on a smooth horizontal surface. The mass of the rope is `0.5` kg. What is the force exerted by the block on the rope?
View SolutionA wooden block of mass 2 kg rests on a soft horizontal floor . When aniron cylinder of mass 25 kg is placed on top of the block , the floor yields steadily , and the block and the cylinder go down with an acceleration of `0.1 ms^(-2)` What is the action of the block on the floor (a) before and (b) after the floor yields ? Take `g = 10 ms^(-2)` . Identify the action reaction pairs in the problem .
View SolutionA wooden block of mass 2 kg rests on a soft horizontal floor . When aniron cylinder of mass 25 kg is placed on top of the block , the floor yields steadily , and the block and the cylinder go down with an acceleration of `0.1 ms^(-2)` What is the action of the block on the floor (a) before and (b) after the floor yields ? Take `g = 10 ms^(-2)` . Identify the action reaction pairs in the problem .
View SolutionTwo blocks are kept in contact on a smooth surface as shown in figure. Draw normal force exerted by A on B.
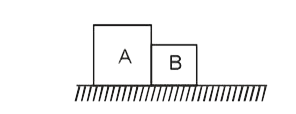
View SolutionAs shown in Fig. three blocks connected together lie on a horizontal frictionless table and pulled to the right with a force F = 50 N. If `m_(1)=5kg, m_(2)=10kg` and `m_(3)=15kg`, find the tensions `T_(1)` and `T_(2)`.

View SolutionThe masses `m_(1) m_(2)` and `m_(3)` of the three bodies shown in fig . Are 5 , 2 and 3 kg respectively Calculate the valuse of tension `T_(1) T_(2)` and `T_(3)` when (i) the whole system is going upward with an acceleration of `2 m//s^(2)` (ii) the whole system is stationary ` (g=9.8 m//s^(2))` .
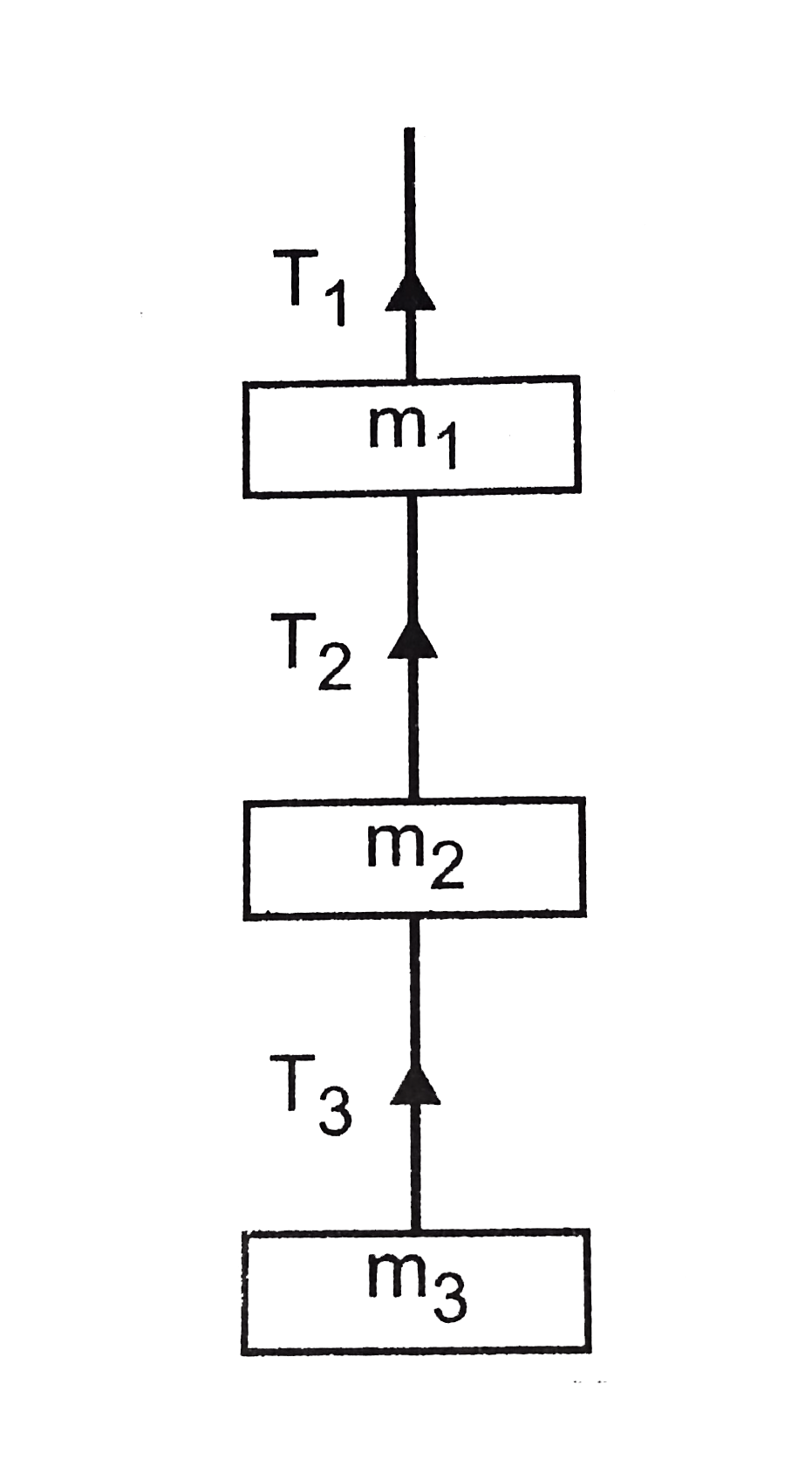 .
.
View SolutionThe masses `m_(1) m_(2)` and `m_(3)` of the three bodies shown in fig . Are 5 , 2 and 3 kg respectively Calculate the valuse of tension `T_(1) T_(2)` and `T_(3)` when (i) the whole system is going upward with an acceleration of `2 m//s^(2)` (ii) the whole system is stationary ` (g=9.8 m//s^(2))` .
 .
.
View SolutionA body `m_(1)` of mass 10 kg is placed on a smooth horizontal table It is connected to a string which passes over a frictionless pulley and carries at the other end , a body `m_(2)` of mass 5 kg What acceleration will be produced in the bodies when the nail fixed on the table is removed ? what will be the tension in the string during the motion of the bodies ? What when the bodies stop ? (g= 9.8 N ? kg ) .
View SolutionA block of mass 100 kg is set into motion on a frictionless horizontal surface with the help of a frictionless pulley and rope system shown in What horizontal force should be applied on the rope to produce an acceleration of `0.1 m//s^(2)`
 .
.
View SolutionTwo blocks of masses 50 kg and 30 kg connected by a massless string pass over a light frictionless pulley and rest on two smooth planes inclined at angles `30^(@)` and `60^(@)` resp . With horizontal .Determine the accelertion in the two blocks and tension in the string `g = 10 m//s^(2)` .
View SolutionWhat is friction? Explain it with an example.
View SolutionHow is friction a component of the contact force?
View SolutionExplain the origin of the force of friction.
View SolutionDefine angle of friction. Deduce its relation with coefficient of friction.
View SolutionDefine angle of repose. Deduce its relation with coefficient of static friction?
View SolutionA block of weight 20 N is placed on a horizontal table and a tension T is applied on the block . Tension can be increased to 8 N before the block begins to slide . A force of 4 N keeps the block moving at constant speed , once it has been set in motion . Find the coefficients of static friction and kinetic friction].
View SolutionA force of 49 N is just sufficient to pull a block of wood weighing 10 kg on a rough horizontal surface. Calculate the coefficient of friction and angle of friction.
View SolutionA cubical block rests on an inclined plance of `mu = (1)/sqrt(3)` . Determine the angle at which the block just slides down the incline .
View SolutionA mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle `0 = 15^(@)` with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
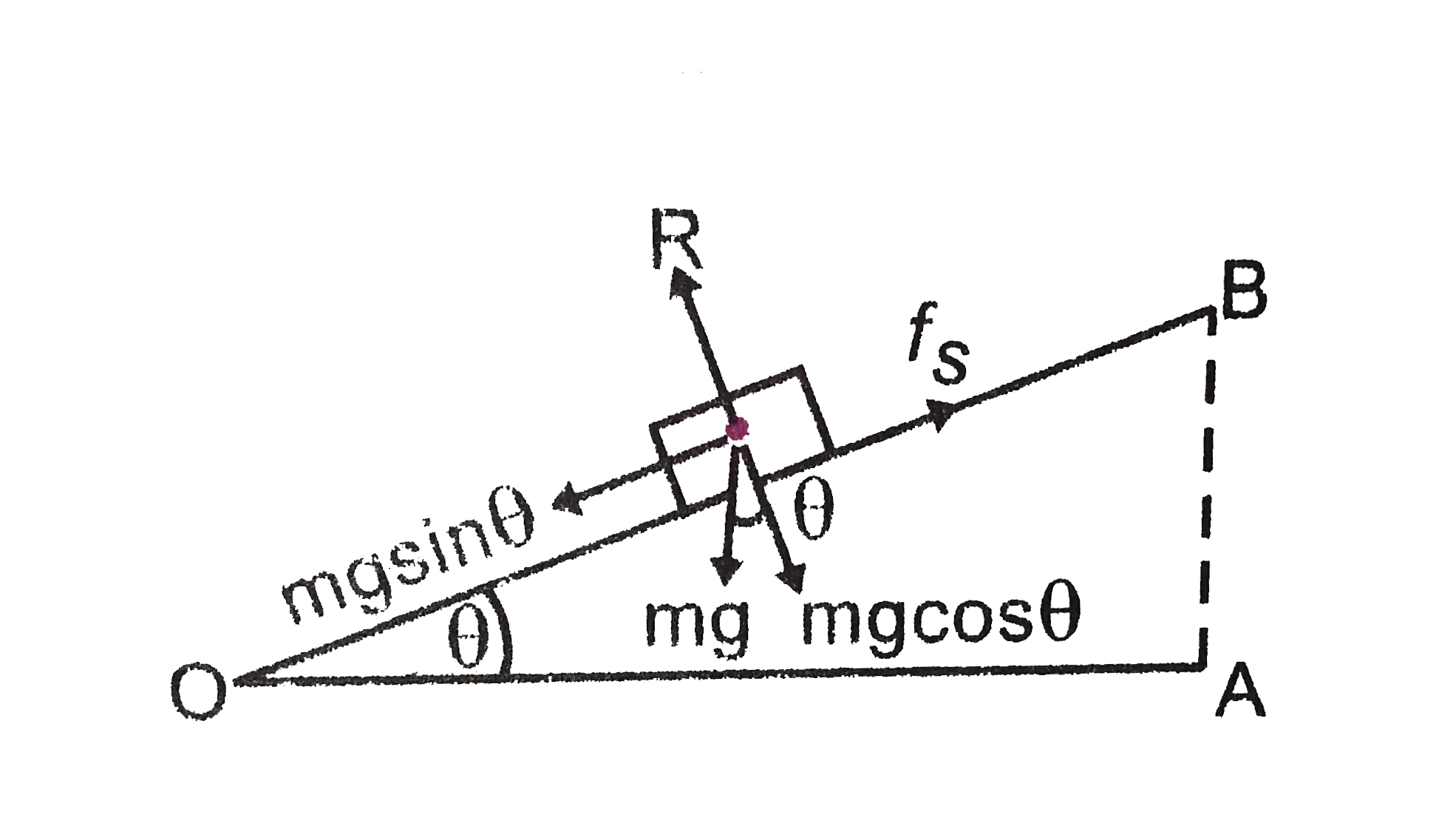
View Solution
Example questions and complete solutions for chapter Laws of Motion of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11