Complete Solutions to Example of chapter Mechanical Properties of fluids of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | Mechanical Properties of fluids |
| SL ARORA | Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
What are fluids ? Give their important characteristic.
View SolutionBoth liquids and gases are fluids.What is the main difference between them?
View SolutionDefine the term thurst. Give its SI unit.
View SolutionShow that liquid in equilibrium of rest exerts normal force on the surface in contact with it.
View SolutionDefine the term pressure.Is it a scalar or a vector? Give its units and dimensions.
View SolutionThe two thigh bones (femur bones) each of cross-sectional area `10 cm^(2)` support the upper part of a human body of mass 40 kg . Estimate the average pressure sustained by the femurs. `g=10m//s^(2)`
View SolutionHow much pressure will man of weight `80kg` f exert on the ground when (i) he is lying and (ii) he is standing on his feet ? Given that the area of the body of the man is `0.6 m^(2)` and that of a foot is `80 cm^(2).`
View SolutionHow much pressure will man of weight `80kg` f exert on the ground when (i) he is lying and (ii) he is standing on his feet ? Given that the area of the body of the man is `0.6 m^(2)` and that of a foot is `80 cm^(2).`
View SolutionDefine the term density. Give its units and dimensions.
View SolutionWhat do you mean by specific gravity or relative density of a substance?
View SolutionState and prove Pascal's law of transmission of fluid pressure.
View SolutionWith the help of a labelled diagram, explain the working of hydraulic brakes.
View SolutionIn car lift compressed air exerts a force `F_1` on a small piston having a radius of 5 cm. This pressure is transmitted to a second piston of radius 15 cm. If the mass of the car to be lifted is 1350 kg, what is `F_1 ?` What is the pressure necessary to ac complish this task ?
View SolutionThe neck and bottom of a bottle are 2 cm and 10 cm in diameter respectively. If the cork is pressed with a force of 1.2 kg f in the neck of the bottle, calculate the force exerted on the bottom of the bottle.
View SolutionTwo syringes of different cross-sections (without needles) filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston and larger piston are 1.0cm and 3.0 cm respectively.
(a) Find the force on the larger piston when a force of 10N is applied to the smaller piston.
(b) The smaller piston is paused in through 6.0 cm, much does the larger piston move out?
View SolutionTwo syringes of different cross-section (without needle filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston an larger piston are `1 cm` and `3 cm` respectively. If a force of 10N is applied to the smaller piston then the force exerted on the larger piston is
View SolutionTwo piston of hydraulic press have diameters of `30.0 cm` and `2.5 cm`. What is force exerted by larger piston , when `50.0kg` wt is placed on the smaller piston ? If the stroke of the smaller piston is `4.0 cm,` through what distance will the larger piston move after 10 strokes?
View SolutionWhat do you understand by buoyancy and centre of buoyancy ?
View SolutionState the law of floatation.
View SolutionState the conditions for the equilibrium of floating bodies.Also discuss the stability of a floating body.
View SolutionThe tip of the iceberg.The density of ice is `917 kg m^-3`. what fraction of ice lies below water?
View SolutionThe density of sea water is `1024 kg m^-3`. What fraction of the iceberg do we see assuming that it has the same density as ordinary ice?(`917 kg m^-3`)?
View SolutionThe density of ice is `0.918 g"cm"^(-3)` and that of water is `1.03 g"cm"^(-3).` An iceberg floats with a portion of `224 m^(3)` outside the surface of water. Find the total volume of the iceberg.
View SolutionA body of mass 6 kg is floating in a liquid with `2//3` of its volume inside the liquid. Find (i) buoyant force acting on the body and (ii) ratio between the density of the body and density of liquid. Take `g=10m//s^(2)`.
View SolutionA body of mass 6 kg is floating in a liquid with `2//3` of its volume inside the liquid.Find ratio between the density of body and density of liquid. Take `g=10 ms^-2`.
View SolutionA piece of pure gold of density `19.3 g cm^(-3)` is suspected to be hollow inside. It weighs 38.250 g in air and 33.865 g in water. Calculate the volume of the hollow portion of the gold, if any:
View SolutionA solid body floating in water has `1//6`th of the volume above surface . What fraction of its volume will project upward if it floats in a liquid of specific gravity `1.2` ?
View SolutionA spring balance reads 10 kg when a bucket of water is suspended from it. What is the reading on the spring balance when (i) an ice cube of mass 1.5 kg is put into the bucket (ii) an iron piece of mass 7.8 kg suspended by another spring is immersed with half its volume inside the water n the bucket. Relative density of iron = 7.8
View SolutionA spring balance reads 10 kg when a bucket of water is suspended from it. What is the reading on the spring balance when (i) an ice cube of mass 1.5 kg is put into the bucket (ii) an iron piece of mass 7.8 kg suspended by another spring is immersed with half its volume inside the water n the bucket. Relative density of iron = 7.8
View SolutionA cube of wood floating in water supports a `200 g` mass at the centre of its top face. When the mass is removed , the mass rises by `2cm.` Determine the volume of cube.
View SolutionA certain block weighs 15 N in air. But is weighs only 12 N when completely immersed in water. When immersed completely in another liquid, it weighs 13 N. Calculate the relative density of (i) the block and (ii) the liquid.
View SolutionA metallic block weighs `15 N` in air. It weights `12 N` when immersed in water and `13 N` when immersed in another liquid. What is the specific gravity of the liquid?
View SolutionA jeweller claims that he sells ornaments made of pure gold that has the relative density of `19.3.`He sells a necklace weighing `25.250 g` f to a person. The clever customer weighs the necklace when immersed in pure water and finds that it weighs `23.075 g` f in water. Is the ornament made of pure gold?
View SolutionA body of density `rho`floats with a volume `V_(1)` of its total volume `V` immersed in one liquid of density `rho_(1)` and with the remainder of volume `V_(2)` immersed in another liquid of density `rho_(2)," ""where"" "rho_(1)gt rho_(2).` Find the relative volumes immersed in two liquids.
View SolutionAn adulterated sample of milk has a density `1032 kg m^(-3)` , while pure milk has a density of `1080 kg m^(-3)` . Then the volume of pure milk in a sample of 10 litres of adulterated milk is
View SolutionA metal plate `5cmxx5cm` rests on layer of castor oil 1mm thick whose coefficient of viscosity is 1.55 `Nsm^(-1)`. Find the horizontal force required to move the plate with a speed of 2`cm^(-1)`.
View SolutionA squre metal plate of 10cm side moves parallel to another plate with a velocity of `10cm s^(-1),` both plates immersed in water. If the viscous force is 200 dyne and viscosity of water is 0.01 poise, what is their distance a part.
View SolutionA flat plate of 20 cm squre moves over another similar plate with a thin layer of 0.4 cm of a liquid between them. If a force of one kg. wt. moves one of the plates uniformly with a velocity with a velcoity of `1 ms^(-1)` calculate the strain rate, sheraing stres and coefficient of viscosity.
View SolutionThe velocity of water in a rier is `18kmh^-1` near the surface. If the river is 5 m deepm, find the shearing stress between the horizontal lyers of water. The coefficient of viscosity of water `=10^-2 poise.
View SolutionExplain the difference between solid friction and viscosity.
View SolutionThe relationship which describes the variation of vapour pressure with temperature is called
View SolutionMention some particle uses of the knowledge of viscosity.
View SolutionState Poiseuille's formula. What are the assumptions used in the derivation of this formula? Derite this formula on the basis of dimensional considerations.
View SolutionCheck the dimensional consistency of the poiseuille's formula for the laminar flow in a tube:
`V=(piR^(4)(p_1-p_2))/(8etal)`
View SolutionA capillary tube of 1mm diameter and 20 cm long is fitted horizontally to a vessel kept full of alcohol of density 0.8 gm//c.c. The depth of centre of capillary tube below the surface of alcohol is 20 cm. If the visosity of oil is `0.12 dyn e cm^(-2)` s, find the amount of liquid that will flow in 5 minuts.
View SolutionIn giving a patient a blood transfusion, the bottle is set up so that the level of blood is 1.3 m above the needle, which has an internal diameter of 0.36 mm and 3 cm in length . If `4.5 cm^(3)` of blood passes through the meedle in one minute, calculate the viscosity of blood. The density of blood is 1020 kg `m^(-3)`.
View SolutionA liquid flows through a pipe of 1.0 mm radius and 10cm length under a pressure `10^4` dyne `cm^(-2)`. Calculate the rate of flow and the speed of the liquid coming out of the tube. The coefficient of viscosity of the liquid is 1.25 centipoise.
View SolutionTwo tubes A and B of length 80 cm and 40 cm have radii 0.1 mm and 0.2 mm respectively are connected in series end to end. If a liquid passing through tow tubes is entering A at a pressure of 82 cm of mercury and leaving B at a pressure of 76 cm of mercury. Find the pressure at the junction of A and B.
View SolutionTwo capillary tubes AB and BC are joined end to end at B, AB is 16cm long and of diameter 4mm whereas BC is 4cm long and of diameter 2mm. The composite tube is held horizontally with A connected to a vessel of water giving a constant head of 3cm and C is open to the air. Calculate the pressure difference between B and C.
View SolutionA large bottle is fitted with a siphon made of capillary glass tubing. Compare the times taken to empty the bottle when it is filled. (i) with water (ii) with petrol of density 0.8 cgs units. The viscosity of water and petrol are 0.1 and 0.2 cgs units repectively.
View SolutionThe level of liquid in a cylinderical vessel is kept constant at 30cm. It has three identical horizontal tubes of length 39cm, each coming out at heights 0,4 and 8cm respectively. Calculate the length of a single overflow tube of the same radius as that of identical tubes which can replace the three when placed horizontally at bottom of the cylinder.
View SolutionThree capillary tubes of the same radius r but of length `l_1, l_2 and l_3` are fitted horizontally to the bottom of a long cylinder containing a liquid at constant head and flowing through these tubes. Find the length of a single overflow tube of the same radius r, which can replaced the three capillaries.
View Solutionwhat is the origin of viscous drag on a body falling through a fluid?
View SolutionState Stoke's law. Deduce Stoke'st law on the basis of dimensional considerations. State the conditions under which Stoke's law is valid.
View SolutionDerive an expression for terminal velocity of the sphere falling under gravity through a viscous medium.
View SolutionA rain drop of radius 0.3 mm falls through air with a terminal viscosity of `1 m s^(-1)`. The viscosity of air is `18 xx 10^(-5)` poise. The viscous force on the rain drop is
View SolutionAn iron ball of radius 0.3cm falls through a column of oil of density 0.94`cm^(-3)` .It is found to attain a terminal velocity of 0.5 `cm^(-1)` Determine the viscosity of the oil, Given that density of iron is 7.8g `cm^(-3)`
View SolutionWith what terminal velocity will an air bubble of density `1 kg m^(-3)` and `0.6` mm diameter rise in a liquid of viscosity `0.15 Ns m^(-2)` and specific gravity `0.9` ? What is the terminal velocity of the same bubble in water of `eta=1xx10^(-3) Ns m^(-2)` ?
View SolutionEight rain drops of radius `1mm` each falling downwards with a terminal velocity of `5 cm s^(-1)` collapse to form a bigger drop. Find the terminal velocity of bigger drop.
View SolutionIf n equal rain droplets falling through air with equal steady velocity of `10 cm s^(-1)` coalesce, find the terminal velocity of big drop formed.
View SolutionFine particles of sand are shaken up in water contained in a tell cylinder. If the depth of water in the cylinder is 24 cm, calculate the size of the largest particle of sand that can remain suspended after the expiry of 40 minutes. Given density of sand =`2.6 g cm^(-3)` and viscosity of water = 0.01 poise. Assume that all the particles are spherical and are of different sizes.
View SolutionA sphere is dropped under gravity through a fluid of viscosity `eta`. Taking the average acceleration as half of the initial acceleration, show that the time to attain the terminal velocity is independent of the fluid density.
View SolutionDistinguish between streamline and turbulent flows. What do you understand by a streamline and tube of flow ? Give important properties of streamlines.
View SolutionWhat is laminar flow of a liquid ?
View SolutionDistinguish between the velocity profiles of non-viscous and viscous liquids.
View SolutionWhat do you mean by critical velocity of a liquid?Derive an expression for it on the basis of dimensional considerations.
View SolutionWhat is Reynold's number? What is its importance ?
View SolutionVerify that the quantity `( rhovd )/(n)`(Reynold's number) is dimensionles.
View SolutionWhat should be the average velocity of a water in a tube of radius 0.005m, so that the flow is just turbulent? The viscosity of water is 0.001 Pa-s.
View SolutionThe flow rate of water from a tap of diameter 1.25 cm is `0.48 L//mi n`. The coefficient of viscosity of water is `10^(-3) Pa-s`. After sometime, the flow rate is increased to `3L//mi n`. Characterise the flow for both the flow rates.
View SolutionWhat is meant by a fluid?
View SolutionObtain the equation of continuity for the incompressible non - viscous fluid having a steady flow through a pipe.
View Solutionin river, the deep water runs…………. And less deep water runs…………
View SolutionWhat are different forms of energy possessed by a flowing liquid? Write expression of them.
View SolutionState and prove Bernoulli's theorem.
View SolutionThe spouting can is something used to demonstrate the variation fo pressure with depth. When the corks are removed from the tubes in the side of the can, water flows out with a speed that depends on the depth. In a certain can, three tubes `T_(1),T_(2)` and `T_(3)` are set at equal distance 'a' above the base of the can. When water contained in this can is allowed to came out of hte tubes, the distance on the horizontal surface are measured as `(x_1),(x_2)` and `(x_3)` .

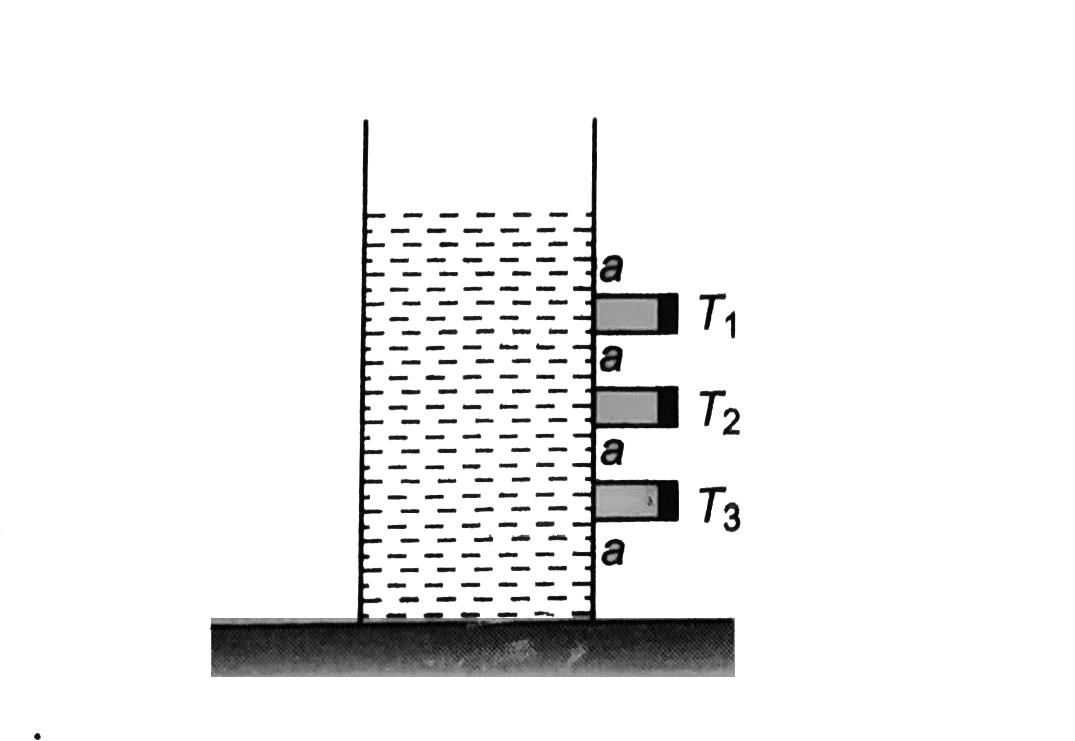
1. speed of efflux is
View SolutionWhat is venturimeter ?
View SolutionDescibe venturimeter's construction and working.
View SolutionWhat is dynamic lift?
View SolutionIf a ball is thrown and gicen a spin , then the path of the ball is curved more than in a usual spin free ball.why?
View Solutionon the basis of Bernoulli's principle, explain the lift of an aircraft wing.
View SolutionIt is observed that during storm, the roof's of some houses are blown off. It is because
View SolutionWater flows through a horizontal pipe of varying area of cross-section at the rate of 10 cubic metre per minute. Determine the velocity of water at a point where radius of pipe is 10cm.
View SolutionWater flow through a horizontal pipe whose internal diameter is `2.0 cm` at a speed of `1.0 ms^(-1)` What should be the diameter of the nozzle, If the water is to emerge at a speed of `4.0ms^(-1)`?
View SolutionAt what speed will the velocity head of stream of water be 40 cm?
View SolutionAt what speed will the velocity head of a stream of water be equal to 20 cm of mercury . Taking `(g=10ms^(-2))`.
View SolutionCalculate the total energy possessed by one kg of water at a point where the pressure is 20 g f/`mn^(2)`, velocity is `0.1 ms^(-1)` and the height is 50 cm above the ground level.
View SolutionThe reading of pressure meter attached with a closed pipe is `3.5 xx 10^(5)Nm^(-2)`. On opening the value of the pipe, the reading of the pressure meter is reduced to `3.0 xx 10^(5) Nm^(-2)`. Calculate the speed of the water flowing in the pipe.
View SolutionA fully loaded Boeing aircraft 747 has a mass of `33xx 10^5 kg`. Its total wing area is `500 m^2`. It is in level flight with a speed of 960 km/h. Estimate the pressure difference between the lower and upper surfaces of the wings.
View SolutionA fully loaded Boeing aircraft has a mass of `3.3xx10^(5) kg`. Its total wing area is `500 m^(2)` . It is in level flight with a speed of `960 km//h`.
(a) Estimate the pressure difference between the lower and upper surfaces of the wings
(b) Estimate the fractional increases in the speed of the air on the upper surfaces of the wing relative to the lower surface. The density of air is `1.2 kg//m^(3)`.
View SolutionCalculate the minimum pressure required to force the blood from the heart to the top of the head (vertical distance = 40 cm). Assume that the denisity of blood to be `1.04 g // cm^(3)`. Friction is to be neglected.
View SolutionWater is flowing through two horizontal pipes of different diameters which are connected together. In the first pipe the speed of water 4 m/s and the pressure is `2.0xx10^(4) N//m^(2)`. Calculate the speed and pressure of water in the second pipe. The diameter of the pipes the diameter of the pipes are 3 cm and 6 cm respectively.
View SolutionThe cross-sectional area of water pipe entering the basement is 4 x `10^(-4) m^(2)`. The pressure at this point is 3 x `10^(5) Nm^(-2)` and the speed of water is 2 `ms^(-1)`. This pipe tapers to a cross-sectional area of 2 x `10^(-4)m^(2)` when it reaches the second floor 8 m above. Calculate the speed and pressure at the 2nd floor
View SolutionThe pressure difference between two points along a horizontal pipe, through which water is flowing, is 1.4 cm of mercury. If ,due to non-unifrom cross-section, the speed of flow of water at the point of greater cross-section is 60 cm `s^(-1)`, calculate the speed at the other point .
View SolutionA point tube is mounted on an aeroplane wing to measure the speed of the plane. The tube contains alcohol and shows a level difference of 40 cm. What is the speed of the plane reative to air ? (sp. Gr. Of alcohol = 0.8 and density of air = 1 kg `m^(-3)`).
View SolutionA pitot tube is fixed in a main pipe of diameter 20 cm and difference of pressure indicated by the gauge is 5 cm of water column. Find the volumn of water passing through the main pipe in one minute.
View SolutionA cylinder of height 20 m is completely filled with water. The velocity of efflux of water through a hole on the side wall of the cylinder near its bottom is (Take `g=10 m s^(-2)`)
View SolutionAt what velocity does water emerge from an orifice in a tank in which gauge pressure is 3 x `10^(5)Nm^(-2)` before the flow starts ? Density of water = 1000 `kgm^(-3)`.
View SolutionA boat strikes an under water rock which punctures a hole 5 cm in diameter in its hull which is 1.5 m below the water line . At what rate in liter per second does water enter ?
View SolutionA drum of 30 cm radius has a capacity of 220 `dm^(3)` of water. It contains 198`dm^3` of water and is placed on a solid block of exactly the same size as of drum .If a small hole is made at lower end of drum perpendicular to its length, find the horizontal range of water on the ground in the beginning. Given g = 980 cm `s^(2)`.
View Solution
Example questions and complete solutions for chapter Mechanical Properties of fluids of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11