Complete Solutions to Exercise of chapter Mechanical Properties of fluids of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | Mechanical Properties of fluids |
| SL ARORA | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Find the pressure exerted at the tip of a drawing pin if it is pushed against a board with a force of `20N.` Assume the area of the tip to be `0.1 mm^(2).`
View SolutionAtmospheric pressure is nearly `100 kPa.` How large the force does the air in a room exert on the inside of a window pan that is `40 cm xx 80 cm`?
View SolutionThe force on a Phonograph needle is `1.2 N.` the point has a circular cross-section whose radius is 0.1 mm. Find the pressure (in atm) it exerts on the recods. Given `1 "atm" = 1.013 xx 10^(5) Pa.`
View SolutionA cylinderical vessel contaning liquid is closed by a smooth piston of mass m. the area of cross-section of the piston is A. if the atmospheric pressure is `P_(0),` Find the pressure of the liquid just below the piston.
View SolutionThe area of the smaller piston of a hydraulic press is `1cm^2` and that of larger piston of a hydralic press is `1cm^2`.How much weight can be raised on the larger piston by a 200 kg f exerted on the smaller piston?
View SolutionThe average mass that must be lifted by a hydraulic press is `80 "kg"`.If the radius of the larger piston is five times that of the smaller piston, what is the minimum force that must be applied?
View SolutionIn a hydraulic press used for compressing cotton the area of the piston is `0.1 m^(2)` and the force exerted along the piston rod is `200 N`. If the area of the larger cylinder is `0.8 m^(2)`, find the pressure produced in the cylinder and the total crushing force exerted on the bale of cotton.
View SolutionAn automobile sack is lifted by a hydraulic jack that consists of two pistons. The large piston is `1 m` in diameter and the small piston is `10 cm` in diameter. If W be the weight of the car, how much smaller a force is needed on the small piston to lift the car?
View SolutionHow much will a body of `70 N ` weight in water if it displaces 20 ml of water ?
View SolutionA solid weighs `6 kg` in air. If its density is `2000 "kg" m^(3)` what will be its apparent weight in water?
View SolutionA solid weighs `10 N` in air. Its weight decreases by `2 N` when weighed in water what is the density of solid?
View SolutionA copper cube of mass `0.50kg` is weighed in water. The mass comes out to be `0.40 kg.` Is the cube hollower solid ? Given density of copper `=8.96 xx 10^(3)"kgm"^(-3)` and density of water `=10^(3) "kgm"^(-3).`
View SolutionA solid floats in water with `3//4` of its volume below the surface of water. Calculate the density of the solid.
View SolutionA piece of wood of relative density `0.25`floats in a pail containing oil of relative density `0.81.`What is the fraction of volume of the wood above the surface of the oil ?
View SolutionA boat having a length of 3 m and breadth of 2 m is floating on a lake. The boat sinks by 1 cm when a man gets on it. The mass of the mas is:
View SolutionWhen a body of mass 240 kg is placed on a ice berg floating in sea water, it is found that the ice berg just sinks. What is the mass of the ice berg ? Take the relative density of ice as 0.9 and that of sea water as 1.02.
View SolutionA cubical block of wood 10 cm on a side floats at the interface between oil and water with its lower surface horizontal and 4 cm below the interface. The density of oil is `0.6 gcm^(-3)`. The mass of block is
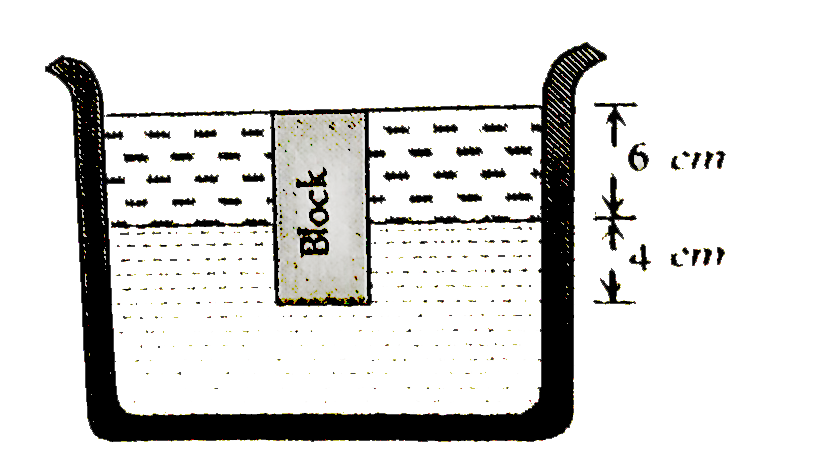
View SolutionA Piece of brass (alloy of zinc and copper) weighs 12.9 g in air. When completely immersed in water it weighs 11.3 g . What is the mass of copper contained in the alloy ? Specific gravity of zinc and copper are 7.1 and 8.9 respectively.
View SolutionA piece of iron floats in mercury. Given that the density of iron is `7.8xx10^(3) "kg"m^(-3)` and that of mercury is `13 xx 10^(3) "kgm"^(-3)`, Calculate the fraction of the volume of iron piece that remains outside the mercury.
View SolutionA metal cube of 5cm side and relative density 9 is suspended by thread so as to be dompletely immersed in a liquid of density `1.2xx10^(3) "kg" m^(-3).` Find the tension in the thread.
View SolutionA cube of side 4cm is just completely immersed liquid A. When it is put in liquid B, it floats with 2 cm outside the liquid. Calculate the ratio fo densities of two liquids.
View SolutionAn iron ball has an air space in it. It weighs 1 kg in air and 0.6 kg in water .Find the volume of air space. Density of iron `=7200 "kgm"^(3).`
View SolutionThe relative velocity of two parallel layers of water is 8 cm/sec. If the perpendicular distance between the layers is 0.1 cm, then velocity gradient will be
View SolutionA circular metal plate of radius 5 cm, rests on a layer of castor oil 2mm thick, whose coeffeicient of viscosity os `15.5 dyn e cm^(-2)s`. Calculate the horizontal force required to move the plate with a speed of `5 cms^(-1)`. Also calculate strain rate and shearing stress.
View SolutionA metal plate of area ` 5 cm ^(2)` is placed on a 0.5 mm thick castor oil layer .If a force of 22,500 dyne is needed to move the plate with a velocity of `3cms^(-1)` Calculate the coefficient of viscosity of castor oil.
View SolutionA metal plate of area `0.02m^(2) ` is lying on a liquid layer of thickness `10^(-3)` m and coeffcient of viscosity 120 poise .Calcualate the horizontal force requirred to move the plate with a speed of `0.025ms^(-1)`
View SolutionIn an experiment with poiseuille's apparatus , the following observation were noted :
Volume of liquid collected per minute `=15cm ^(3)`
Head of liquid =30cm, Length of tube =25 cm
Diameter of tube =0.2 cm, Density of liquid =`2.3 gcm^(-3)`
Find the coefficient of viscosity of the liquid.
View SolutionWater at `20^(@)` C is escaping from a cistern by ways of a horizontal capillary tube 10 cm long and 0.4 mm in diameter ,at a distance of 50 cm below the free surface of water in the cistern .Calculate the rate at which the water is escaping .Coefficient of viscosity of water at `20^(@)C` =0.001 decapoise .
View SolutionWater is conveyed through a horizontal tube 8 cm in diameter and 4 kilometer in length at the rate of 20 litre/s Assuming only viscous resistance , calculate the pressure required to maintain the flow . Coefficient of viscosity of water is 0.001 pa s
View SolutionAlcohol flows through two capillary tubes under a constant pressure head the diameters of the two tubes are in the ratio of `4:1` and the lengths are in the ratio `4:1` Compare the rates of flow of alcohols through the two tubes .
View SolutionShow that if two capillaries if radii `r_(1)and r_(2)` having lenths `l_(1)and l_(2)` respectively are set in series ,the rate of flow Q is given by
`Q=(pip)/(8eta)[(l_(1))/(r_(1)^(4))+(l_(2))/(r_(2)^(4))]^(-1)`
where p is the pressure difference across the arrangement and `eta` is the cofficient of viscosity of the liquid.
View SolutionThere capillaries of length l, `2l` and `l//2` are connected in series. Their radii are r, `r//2` and `r//3` respectively. If stream line flow is maintained and the pressure difference across the first capillary tube is `P_(1)`, find the pressure difference across (i) the second and (ii) the thired capillary tube.
View SolutionThere capillaries of length l, `2l` and `l//2` are connected in series. Their radii are r, `r//2` and `r//3` respectively. If stream line flow is maintained and the pressure difference across the first capillary tube is `P_(1)`, find the pressure difference across (i) the second and (ii) the thired capillary tube.
View Solutionfind the terminal velocity of a steel ball 2mm in diameter falling through glycerine. Relative density of steel =8, relative density of glycerine =1.3 and viscosity of glycerine=8.3 poise.
View SolutionA gas bubble of diameter 2 cm rises steadily at the rate of `2.5 mm s^(-1)` through a solution of density 2.25 g `cm^(-3) `. Calculate the coefficient of viscosity of the liquid. Neglect the density of the gas.
View SolutionA drop of water of radius `0.0015 mm` is falling in air. If the coefficient of viscosity of air is `1.8 xx 10^(-3)kg//m^(3)`, what will be the terminal velocity of the drop? Density of water `= 1.0 xx 10^(3) kg//m^(3)` and `g = 9.8 N//kg`. Density of air can be neglected.
View SolutionThe terminal velocity of a copper ball of radius `2mm` falling through a tank of oil at `20^(@)C` is `6.5cm//s`. Find the viscosity of the oil at `20^(@)C`. Density of oil is `1.5xx10^(3)Kg//m^(3)`, density of copper is `8.9xx10^(3)Kg//m^(3)`.
View SolutionA spherical glass ball of mass `1.34xx10^(-4)` kg and diameter `4.4xx10^(-3)` m takes 6.4 s to fall steadily through a height of 0.381 m inside a large volume of oil of specific gravity 0.943 Calculate the viscosity of oil.
View SolutionTwo exactly similar rain drops falling with terminal velocity of `(2)^(1//3) ms^(-1) `coalesce to from a bigger drop Find the new terminal velocity of the bigger drop.
View SolutionWhat should be the maximum average velocity of water in a tube of diameter 0.5 cm , so that the flow is laminar? The viscosity of water is `0.00125 Nsm^(-2)`.
View SolutionWater is following in a pipe of radius 1.5 cm with an average velocity of 15`cms^(-1)`. What is the nature of flow? Given coeffcient of viscosity of water is `10^(-3)` kg `m^(-1)s^(-1)` and its density is`10^(3) kgm^(-3)`.
View SolutionWater flows at a speed of `6ms^(-1)` through a tube of radius 1 cm. Coefficient of viscosity of water at room temperature is 0.01 poise. What is the nature of the flow?
View SolutionFind the critical velocity for air flowing through a tube of 2cm diameter .For air `rho=1.3xx10^(-3)gcm^(-3) and eta=181xx10^(-6)` poise
View SolutionWater flows through a horizontal pipe of varying cross-section at the rate of 20 litres per minutes , determine the velocity of water at a point where diameter is `4 cm`
View SolutionA garden hose having an internal diameter 2.0 cm is connected to a lawn sprinkle that consists of an enclosure with 24 holes , each 0.125 cm in diameter. If water in the hose has a speed of `90.0 cm s^(-1)` , find the speed of the water having the sprinkler hole.
View SolutionIn normal adult the average speed of the though the aorta (which has a radius of 0.9 cm) is `0.33ms^(-1)` From the aorta ,the blood goes into major arteries which are 30 in number ,each of radius 0.5 Calculate the speed of blood through the arteries.
View SolutionVelocity of flow of water in a horizontal pipe is `4.9 ms^(-1)` Find the velocity head of water.
View SolutionThe reading of a pressure meter attached to a horizontal closed pipe is `3 xx 10^(5) Nm^(-2)`. This reading falls to `1 xx 10^(5) N m^(-2)` when the valve is opened. What is the speed of water flowing in the pipe?
View Solutionwater enters at one end of a horizontal pipe of non-uniform cross -section with a velocity of `0.4 ms^(-1)` and leaves the other end with a velocity of `0.6 ms^(-1)` The pressure of water at the first end is `1500Nm^(-2)` Calculate the pressure at the other end Density of water `=1000kgm^(-3)`
View SolutionWater is flowing with a speed of `2m//s` in a horizontal pipe with cross-sectional area decreasing from `2xx10^(-2) m^(2)` to `0.01 m^(2)` at pressure `4xx10^(4)` pascal. What will be the pressure at smaller cross-section?
View SolutionA tank cotaining water has an orifice 10 m below the surface of water in the tank . If there is no wastage of energy ,find the speed of discharge.
View SolutionCalculate speed of efflux of kerosene from an orifice of a tank in which pressure is 4 atmosphere .Density of kerosene is 0.72 kg per litre .One atmosphere `=1 kg f cm^(-2)`.
View SolutionWater flows at the rate of 4 litres per second through an orifice at the bottom of tank which contains water 720 cm deep .Find the rate of escape of water if additional pressure of 16 `kgf/ (cm)^2` is applied at the surface of water.
View SolutionThe diameter of a pipe at two points , where a venturimeter is connected is 8 cm and 5 cm and the difference of levels in it is 4 cm. Calculate the volume of water flowing through the pipe per second.
View SolutionA venturimeter is `37.5 cm`. Diameter in mains and `15 cm`. Diameter in throat. The difference between the pressure of water in the mais and the throat is `23 cm` of Hg. Find the discharge in `litres//minunte`. Sp. Gravity of Hg. `13.56`.
View SolutionA soap film is formed on a rectangular frame of length 7 cm dipping in soap solution. The frame hanges from the arm of a balance. An extra weight of 0.38 g is to be placed in the opposite pan to balance the pull on the frame. Calculate the surface tension of the soap solution. `"Given" g= 980 "cms"^(-2).`
View SolutionA soap film is on a rectangular wire ring of size `5cm ** 4 cm`. If the size of the film is changed to `5cm xx 5cm`, then calculate the work done in this process. The surface tension of soap film is `5 xx 10^(-2) Nm^(-1)`.
View SolutionA soap bubble is blown to a diameter of 7 cm. if 36960 ergs of work is done in blowing if further find the new radius, if surface tension of the soap solution is 40 dynes/cm.
View SolutionA soap bubble of radius `1//sqrtpi "cm"` is expanded to radius `2//sqrtpi "cm".` Calculate the work done. Surface tension of soap solution `=30 "dyne"" "cm^(-1).`
View SolutionWhat amount of energy will be liberated if `1000` droplets of water, each of diameter `10^(-8)cm,` coalesce to form a bigger drop. Surface tension of water is `0.072"Nm"^(-1).`
View SolutionCalculate the amount force required to take away a flat plate of radius 5 cm from the surface of water . Given surface tension of water `= 72 "dyne"" "cm^(-1).`
View SolutionA thin wire is bent in the form of a ring of diameter 3.0 cm . The ring is placed horizontally on the surface of soap solution and then raised up slowly . How much upward force is necessary to break the vertical film formed between the ring and the solution ? surface tension of a soap solution `=3.0 xx 10^(-2) "Nm"^(-1).`
View Solutionthe langth of a needle floating on water is 2.5 cm . How much minimum force in addition to the weight of the needle, will be needed to lift the needle above the surface of water ? Surface tension of water `=7.2 xx 10^(-4) "Ncm"^(-1).`
View SolutionA rectangular plate of dimensions `6cm xx 4 cm` and thickness 2 mm is placed with its largest face flat on surface of water . (i) What is the downward force on the plate due to surface tension ? Surface tension of water `=7.0 xx10^(-2) "Nm"^(-1)` (ii) If the plate is placed vertical so that the longest side just touches the water surface, find the downward force on the plate.
View SolutionA rectangular plate of dimensions `6cm xx 4 cm` and thickness 2 mm is placed with its largest face flat on surface of water . (i) What is the downward force on the plate due to surface tension ? Surface tension of water `=7.0 xx10^(-2) "Nm"^(-1)` (ii) If the plate is placed vertical so that the longest side just touches the water surface, find the downward force on the plate.
View SolutionWhat would be the gauge pressure inside an air bubble of `0.2 mm` radius situated just below the surface of water ? Surface tension of water is `0.07 "Nm"^(-1).`
View Solutionthe pressure of air in a soap bubble of 0.7 cm diameter is 8 mm of water above the atmospheric pressure . Calculate the surface tension of soap solution .take `g= 9.8 "ms"^(-2).`
View SolutionCalculate the total pressure inside a spherical air bubble of radius 0.2 mm formed inside water at depth of 10 cm. Surface tension of water at a depth of 30 cm is `70 "dyne" cm^(-1),` barometric pressure is 76 cm, density of mercury is `13.6 g "cm"^(-3) "and " g= 980 "cms"^(-2).`
View SolutionCalculate the total pressrue inside a spherical air bubble of radius 0.1mm at a depth of 10 cm below the surface of a liquid of density `1.1 g "cm"^(-3)` and surface tension `50"dyne"" "cm^(-1).` Height of Hg barometer `=76"cm".`
View SolutionFind the difference in excess pressure on the inside and outside of a rain drop if its diameter change from 0.03 cm to 0.0002 cm by evaporation . Surface tension of water is `72"dyne"" "cm^(-1).`
View SolutionWhat is the pressure inside a vapour bubble of radius `10^(-3)` m formed in boiling wate? Surface tension of water at `100^(@)C "is" 0.059 "Nm"^(-1) "and" 1 "atm" = 101325 "nm"^(-2).`
View SolutionThere is an air bubble of radius `1.0 mm ` in a liquid of surface tension `0.075"Nm"^(-1)` and density `10^(3) "kgm"^(-3)`. The bubble is at a depth of `10.0 cm` below the free surface of a liquid. By what amount is the pressure inside the bubble greater than the atmospheric pressure?
View SolutionAn ancient building has a done of 5m radius and uniform but small thickness. The surface tension of its masionary structure is about `500 "Nm"^(-1)` . Treated as hemisphere, find the maximum load that dome can support.
View SolutionThe radius of capillary tube is 0.025 mm. If is held vetically in a liquid whose density is `0.8 xx 10^(3) "kg" m^(-3),` surface tension is `3.0xx10^(-2)"Nm"^(-1)` and for which the cosine of the angle of contact is 0.3. Determine the height upto which the liquid will rise in the tube . Given `g=10"ms"^(-2).`
View SolutionA capillary tube of inner radius `0.5 mm` is dipped keeping it vertical in a mercury of specific gravity 13.6, surface tension `545 dyn e//cm` and angle of contact `135^(@)` . Find the depression or elevation of liquid in the tube.
View SolutionCalculate the diameter of a capillary tube in which mercury is derpessed by 1.21 cm. Given surface tension for mercury is `540 xx 10^(-3) "Nm"^(-1).` the angle of contact with glass is `140^(@)` and density of mercury is `13.6 xx 10^(3) "kg" m^(-3).`
View SolutionThe tube of mercury barometer is 4mm in diameter. How much error does the surface tension cause in the reading? Surface tension of mercury = `540" x "10^(-3) Nm^(-1)`, angle of contact = `135^(@)`. Density of mercury `= 13.6 xx 10^(3)kg m^(-3)`.
View SolutionA tube of 1mm bore is dipped into a vessel containing a liquid of density `rho = 800 kg m^(-3)` and of surface tension , `S=49 xx 10^(-3)Nm^(-1)` and angle of contact , `theta = 0^(@)`. The tube is held inclined to the verticle at an angle of 60^(@), find the height to which the liquid can rise and the length which the liquid will oc cupy in the tube.
View SolutionA capillary tube whose inside radius is 0.6 mm is dipped in water in a bucket of surface tension 75 dyn e `cm^(-1)` To what height is the water raised in the capillary tube above the level water in bucket ? What is the weight of water raised ?
View SolutionA `U-`tube is made up of capillaries of bores `1 mm` and `2 mm` respectively. The tube is held vertically and partically filled with a liquid of surface tension `49 "dyne"//"cm"` and zero contact angle. Calculate the density of the liquid of the difference in the levels of the meniscus is `1.25 cm`.
View SolutionA hydraulic automobile lift is designed to lift cars with a maximum mass of 300 kg. the area of cross-section of the piston carrying the load is `425cm^(3)`. What maximum pressure would smaller piston have to bear?
View SolutionRadius of one arm of hyddraulic lift is four times of radius of other arm. What force should be applied on narrow arm to lift 100 kg?
View SolutionA bubble is at the bottom of the lake of depth h. As the bubble comes to sea level, its radius increases three times. If atmospheric pressure is equal to l metre of water column, then h is equal to
View SolutionA liquid X of density `3.36 g//cm^(3)` poured in a U-tube which contains Hg. Another liquid Y is poured in left arm with heght 8 cm upper levels of X and Y are same. What is density of Y?
View SolutionEqual masses of water and a liquid of density 2g/cm3 are mixed together. The density of mixture is:
View SolutionWhen equal volumes of two metals are mixed together the specific gravity of alloy is 4. When equal masses of the same two metals are mixed together the specific gravity of the alloy becomes 3. find specific gravity of each metal?
(specific gravity `=("density of substance")/("density of water"))`
View SolutionThe density of ice is `9.2 xx 10^2 kg/ m^3`. If a chunk displaces `10^-2 m^3`, the buoyant force on the ice is most nearly
View SolutionA piece of wood is taken deep inside a long column of water and released. It wil move up
View SolutionIf there were no gravity, which of the following will not be there for a fluid ?
View SolutionAn ice cube containing a piece of lead floats in water What would be the effect on the level of water if the ice cube melts ?
View SolutionA body of mass 15 kg is dropped into the water. If the apparent weight of the body is 107 N, then the applied thrust will be
View SolutionIf the weight of a body in vacuum is w and `w_(1)` and `w_(2)` are weights when it is immersed in a liquid of specific gravity `rho_(1)` and `rho_(2)` respectively, then find the relation among `w,w_(1)and w_(2)`
View SolutionA glass beaker is placed partially filled with water in a sink it has a mass of 390 gm and an interior volume of `500 cm^(2)` when water starts filling the sink, it is found that if beaker is less than half full it will float but if it is more than half full it remains on the bottom of the sink as the water rises to its rim, what is the density of the material of which the beaker is made?
View SolutionA glass of soft drink with some ice-cubes floating in it, is taken in an elevator which is accelerating down. Then, the portion of ice outside the soft drink
View SolutionThe unit of the coefficient of viscosity in S.I. system is
View SolutionMotion of fluid in a tube is best descrined by
View SolutionThe rate of flow of liquid in a tube of radius r, length l, whose ends are maintained at a pressure difference P is `V = (piQPr^(4))/(etal)` where `eta` is coefficient of the viscosity and Q is
View SolutionTwo capillary of length L and 2L and of radius R and 2R are connected in series. The net rate of flow of fluid through them will be (given rate to the flow through single capillary,
`("X"=(pi"PR"^(4))/(8eta"L"))`
View SolutionThe rate of flow of water in a capillary tube of length l and radius r is V. The rate of flow in another capillary tube of length 21 and radius 2 r for same pressure difference would be
View SolutionAn object is moving through the liquid. The viscous damping force acting on it is proportional to the velocity. Then dimensions of constant of proportionality are
View Solution
Exercise questions and complete solutions for chapter Mechanical Properties of fluids of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11