Complete Solutions to EXERCISE 9.1 of chapter DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITY of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITY |
| SURA PUBLICATION | EXERCISE 9.1 |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
`lim_(xto2)(x-2)/(x^(2)-x-2)`

View Solution`lim_(xto2)(x-2)/(x^(2)-4)`

View Solution`lim_(xto0)(sqrt(x+3)-sqrt3)/x`

View Solution`lim_(xto-3)(sqrt(1-x)-2)/(x+3)`

View Solution`lim_(xto0)(sinx)/x`

View Solution`lim_(xto0)(cosx-1)/x`

View Solution`lim_(xrarr3)4-x.`
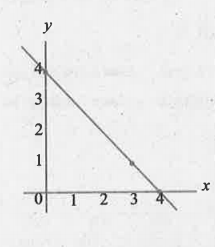
View Solution`lim_(xrarr1)(x^2+2)`
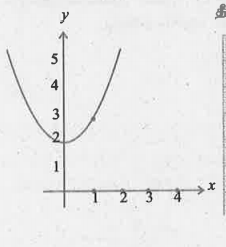
View Solution`lim_(xrarr3)4-x.`

View Solution`lim_(xrarr1)(x^2+2)`

View Solution`lim_(xrarr3)1/(x-3)`
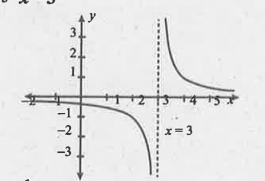
View Solution`lim_(xrarr5)|x-5|/(x-5)`
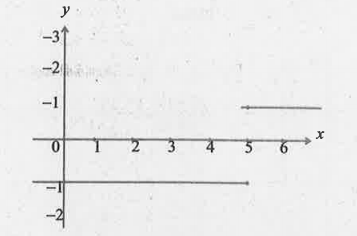
View Solution`lim_(xrarr1)sinpix`
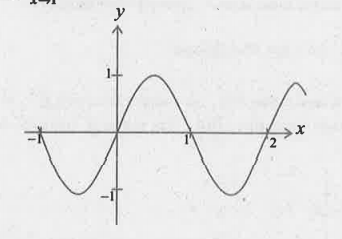
View Solution`lim_(xrarrpi/2)tanx`
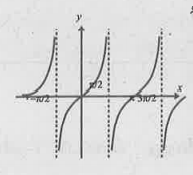
View Solution`f(x)={{:(x^(2)", "xle2),(8-2x", "2ltxlt4),(4", "xge4):}`
View Solution`f(x)={{:(sinx", "xlt0),(1-cosx", "0lexlepi),(cosx", "xgtpi):}`
View SolutionSketch the graph of a function f that satisfies the given values:
f(0) is underfined `lim_(xto0)f(x)=4`,
f(2) = 6, `lim_(xto2)f(x)=3`
View SolutionSketch the graph of a function f that satisfies the given values:
f(-2) = 0 , f(2) = 0 , `lim_(xto-2)f(x)=0`
`lim_(xto2)f(x)` does not exist.
View SolutionWrite a brief description of the meaning of the notation `lim_(x to 8) f(x)=25`
View SolutionIf f(2) = 4, can you conclude anything about the limit of f(x) as x approaches 2 ?
View SolutionIf the limit of f(x) as x approaches 2 is 4, can you conclude anything about f(2)? Explain reasoning.
View SolutionEvaluate : `lim_(xto3)(x^(2)-9)/(x-3)` if it exists by finding `f(3^(-))andf(3^(+))`.
View SolutionVerify the existence of `lim_(xto1)f(x)`, where
`f(x)={{:((|x-1|)/(x-1)","" for "xne1),(0","" for "x=1):}`
View Solution
EXERCISE 9.1 questions and complete solutions for chapter DIFFERENTIAL CALCULUS - LIMITS AND CONTINUITY of SURA MATHS (TAMIL ENGLISH) of Class 11