Complete Solutions to EXERCISE of chapter வகை நுண்கணிதம் எல்லைகள் மற்றும் தொடர்ச்சித் தன்மை of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | வகை நுண்கணிதம் எல்லைகள் மற்றும் தொடர்ச்சித் தன்மை |
| SURA PUBLICATION(TAMIL) | EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
`lim_(xrarr2)(x-2)/(x^2-x-2)`

View Solution`lim_(xrarr2)(x-2)/(x^2-4)`

View Solution`lim_(xrarr0)(sqrt(x+3)-sqrt3)/(x)`

View Solution`lim_(xrarr-3)(sqrt(1-x)-2)/(x+3)`

View Solution`lim_(xrarr0)(sin x)/(x).`

View Solution`lim_(xrarr0)(cosx-1)/(x)`

View Solution`lim_(xrarr3)4-x.`
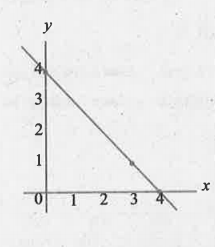
View Solution`lim_(xrarr1)(x^2+2)`
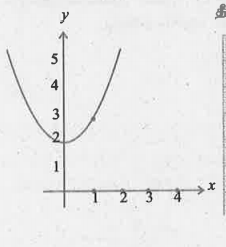
View Solution`lim_(xrarr2)f(x)` இங்கு `f(x)= {(4-x,, x!=2), (0,,x=2):}`
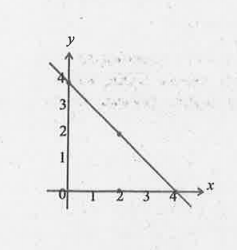
View Solution`lim_(xrarr1)f(x)` இங்கு `f(x)= {(x^2+2,, x!=1), (1,, x=1):}`
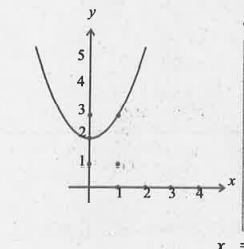
View Solution`lim_(xrarr3)1/(x-3)`
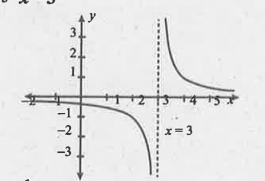
View Solution`lim_(xrarr5)|x-5|/(x-5)`
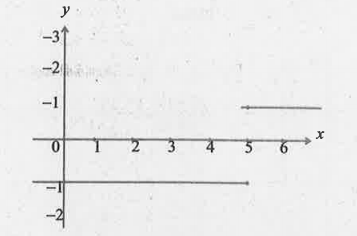
View Solution`lim_(xrarr1)sinpix`
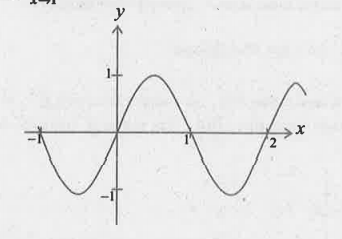
View Solution`lim_(xrarr0)secx`
View Solution`lim_(xrarrpi/2)tanx`
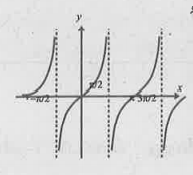
View Solution`f(x)={(sin x,x<0),(1-cosx, olexlepi), (cosx,x>pi):}`
View Solutionகொடுக்கப்பட்ட மதிப்புகளை நிறைவு செய்யும் சார்பின் வரைபடம் வரைக. (i) f(0)வரையறுக்கப்படவில்லை `lim_(xrarr0) f(x)=4``f(2)=6``lim_(xrarr2)f(x)=3` (ii) f(-2)=0 f(2)=0 `lim_(xrarr-2) f(x)=0`, `lim_(xrarr2)f(x)` என்ற எல்லை மதிப்பு இல்லை
View Solution`lim_(xrarr8)f(x)=25` என்ற குறியீட்டு முறையின் பொருளைச் சுருக்கமாக விளக்குக.
View Solutionf(2)=4, எனில் x-ன் மதிப்பு 2-ஐ நெருங்கும் போது f(x)-ன் எல்லை மதிப்பைப் பற்றி ஏதேனும் முடிவு செய்ய இயலுமா?
View Solutionx-ன் மதிப்பு 2-ஐ நெருங்கும் போது f(x)-ன் எல்லை மதிப்பு 4 எனில், f(2)-ஐப் பற்றி ஏதேனும் முடிவு செய்ய இயலுமா? விடைக்கான விளக்கம் தருக.
View Solution`f(3^-)` மற்றும் `f(3^+)` கண்டு, அவற்றின் மூலம் `lim_(xrarr3) (x^2-9)/(x-3)`-க்கு மதிப்பு இருக்குமானால் அந்த மதிப்பைக் காண்க.
View Solution`f(x)={(|x-1|/(x-1),,x!=1),(0,,x=1):}` எனில் `lim_(xrarr1)f(x)`-ன் மதிப்பு உள்ளதா என்பதைச் சரிபார்க்க.
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(xrarr2)(x^4-16)/(x-2)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(xrarr1)(x^m-1)/(x^n-1)`, m, n முழு எண்கள்.
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(sqrtxrarr3)(x^2-81)/(sqrtx-3)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(hrarr0)(sqrt(x+h)-sqrtx)/(h)` x>0
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(xrarr5)(sqrt(x+4)-3)/(x-5)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(xrarr2)(1/x-1/2)/(x-2)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(xrarr1)(sqrtx-x^2)/(1-sqrtx)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(xrarr0)(sqrt(x^2+1)-1)/(sqrt(x^2+16)-4)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க.`lim_(xrarr0)(sqrt(1+x)-1)/(x)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க.`lim_(xrarr1)(root3(7+x^3)-sqrt(3+x^2))/(x-1)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(xrarr2)(2-sqrt(x+2))/(root(3)2-root(3)(4-x))`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(xrarr0)(sqrt(1+x^2)-1)/(x)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(xrarr0)(sqrt(1+x)-1)/(x^2)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(xrarr5)(sqrt(x-1)-2)/(x-5)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(xrarra)(sqrt(x-b)-sqrt(a-b))/(x^2-a^2)(a>b)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(xrarr3)(x^2-9)/(x^2(x^2-6x+9))`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க.`lim_(xrarrinfty)(3)/(x-2)-(2x+11)/(x^2+x-6)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க.`lim_(xrarrinfty)(x^3+x)/(x^4-3x^2+1)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(xrarrinfty)(x^4-5x)/(x^2-3x+1)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க.`lim_(xrarrinfty)(1+x-3x^3)/(1+x^2+3x^3)`
View Solutionபின்வரும் எல்லைகளின் மதிப்பைக் காண்க. `lim_(xrarrinfty)(x^3/(2x^2-1)-x^2/(2x+1))`
View Solutionமீன் வள அறிவியலின் முக்கிய பிரச்சனை நீரோடைகளில் உள்ள முட்டையிடத் தகுதியான மீன்களின் எண்ணிக்கையைக் கணக்கிட்டு இந்தத் தகவலைப் பயன்படுத்தி இனப்பெருக்கக் காலத்தில் ஆற்றுக்குள் நுழையும் மீன் பிடிப்புக்குத் தகுந்த மீன்களின் எண்ணிக்கையைக் கணக்கிடுவதாகும். S என்பது முட்டையிடும் நிலையில் உள்ள மீன்களின் எண்ணிக்கை மற்றும் R என்பது மீன் பிடிப்புக்கு தகுந்த மீன்களின் எண்ணிக்கையாகும். "பிவர்ட்டன் ஹோலட்" - ன் இனப்பெருக்கச் சார்பு `R(S ) = S/(alphaS+beta)` இங்கு `alpha ` , `beta` என்பன மிகை மாறிலிகள் இந்தச் சார்பு இனப்பெருக்க நிலையில் இருக்கும் மீன்களின் எண்ணிக்கை தேவையான அளவு அதிகரிக்கும் போது அறுவடைக்குத் தகுந்த மீன்களின் எண்ணிக்கை தோராயமாக மாறிலியாக அமையும் என நிறுவுக.
View Solutionஒரு தொட்டியில் 5000 லிட்டர் நல்ல நீர் உள்ளது என்க. ஒரு லிட்டருக்கு 30 கி அளவு உப்பு கொண்ட உவர் நீர் 25லி/நிமிடம் என்ற அளவில் தொட்டியில் செலுத்தப்படுகின்றது. t நிமிடங்களில் இந்த உவர் நீரின் அடர்த்தி (கிராம் / லிட்டர்) `C(t) = (30t)/(200+t)` என தரப்பட்டுள்ளது. `t rarrinfty` எனில் அடர்த்தி எவ்வாறு மாறும்?
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarrinfty)(1+1/x)^(7x)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க.`lim_(xrarrinfty)(1+x)^(1/(3x))`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க `lim_(xrarrinfty)(1+k/x)^(m/x)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க `lim_(xrarrinfty)((2x^2+3)/(2x^2+5))^(8x^2+3)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarrinfty)(1+3/x)^(x+2)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)sin^3(x/2)/x^3`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(sinalphax)/(sinbetax)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(tan2x)/(sin5x)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(alphararr0)sin(alpha^n)/(sinalpha)^m`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(sin(a+x)-sin(a-x))/x`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(sqrt(x^2+a^2)-a)/(sqrt(x^2+b^2)-b`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(2arc sinx)/(3x)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(1-cosx)/(x^2)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(tan2x)/(x)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(2^x-3^x)/(x)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(3^x-1)/(sqrt(x+1)-1`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(1-cos^2x)/(xsin2x)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க.`lim_(xrarrinfty)x[3^(1/x)+1-cos(1/x)-e^(1/x)]`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarrinfty){x[log(x+a)-log(x)]}`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarrpi)(sin3x)/(sin2x)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarrpi)(1+sinx)^(2cosecx)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(sqrt2-sqrt(1+cosx))/(sin^2x)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(sqrt(1+sinx)-sqrt(1-sinx))/(tanx)`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarrinfty)((x^2-2x+1)/(x^2-4x+2))^x`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(e^x-e^(-x))/sinx`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(e^(ax)-e^(bx))/x`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(sinx(1-cosx))/x^3`
View Solutionபின்வருவனவற்றின் மதிப்பைக் காண்க. `lim_(xrarr0)(tanx-sinx)/x^3`
View Solution`f(x) = 2x^2+3x-5` `RR`-ன் எல்லா புள்ளிகளிலும் தொடர்ச்சியானது என நிறுவுக.
View Solutionகொடுக்கப்பட்ட சார்புக்குக் கொடுக்கப்பட்ட புள்ளி `x_ 0` - இல் தொடர்ச்சியானதா அல்லது தொடர்ச்சியற்றதா எனக் காரணத்துடன் கூறுக. (i) `x_0=1,f(x) = {((x^2-1)/(x-1),, x!=1),(2,,x=1):}` (ii) `x_0=3,f(x) = {((x^2-9)/(x-3),, x!=3),(5,,x=3):}`
View Solution`{((x^3-1)/(x-1),, x!=1),(3,,x=1):}` என்ற சார்பு `(-infty, infty)`-இல் தொடர்ச்சியானது எனக்காட்டுக.
View Solution`f(x) ={((x^4-1)/(x-1),, x!=1),(alpha,,x=1):}` என வரையறுக்கப்பட்ட சார்பில் x=1-இல் சார்பு தொடர்ச்சியானது எனில் `alpha`-ன் மதிப்பு காண்க.
View Solution`f(x) ={(0,, x<0),(x^2,,0lex<2),(4,,xge2):}` என்ற சார்பின் வளைவரையை வரைக. இச்சார்பு `(-infty,infty)`-ல் தொடர்ச்சியானது என நிறுவுக.
View Solutionf மற்றும் g தொடர்ச்சியான சார்புகள் மேலும் f (3) = 5 மற்றும் `lim_(xrarr3)[2f(x)-g(x)]=4`, எனில் g(3)-இக் காண்க.
View Solutionf பின்வருமாறு வரையறுக்கப்பட்டுள்ளது :`f(x)={(0.,x<0,),(x,,0lex<1,),(-x^2+4x-2,,1lex<3,),(4-x,,xge3):}` இந்தச் சார்பு தொடர்ச்சியானதா?
View Solution`g(x)={(x^2-b^2 ,x<4),(bx+20,xge4):}` என்ற சார்பு `(-infty, infty)` -ல் தொடர்ச்சியானது எனில் மாறிலி b - ஐக் காண்க.
View Solution`f(x)= xsin(pi/x)` என்க. f(0)-ன் எந்த மதிப்புக்கு எல்லா இடங்களிலும் தொடர்ச்சியானதாக இருக்கும்?
View Solution`f(x)= (x^2-1)/(x^3-1)` என்ற சார்பு x=1-ல் வரையறுக்கப்படவில்லை f(1)-ன் எந்த மதிப்பிற்கு x = 1-ல் f தொடர்ச்சியானதாக இருக்கும்?
View Solution`lim_(xrarrinfty) sin x/x`
View Solution`lim_(xrarrpi/2) (2x-pi)/cosx`
View Solution`lim_(xrarr0) (sqrt(1-cos2x)/x)`
View Solution`lim_(thetararr0) sinsqrttheta/sqrtsintheta`
View Solution`lim_(xrarrinfty)((x^2+5x+3)/(x^2+x+3))^x`
View Solution`lim_(xrarrinfty)sqrt(x^2-1)/(2x+1)=`
View Solution`lim_(xrarrinfty)(a^x-b^x)/x=`
View Solution`lim_(xrarr0)(8^x-4^x-2^x+1^x)/x^2=`
View Solution`f(x)=x(-1)^(⌊1/x⌋) , xle0,` இங்கு x என்பது x-க்குச் சமமான அல்லது குறைவான மீப்பெரு முழு எண்,எனில் `lim_(xrarr0)f(x)`-ன் மதிப்பு
View Solution`lim_(xrarr3)`⌊`x`⌋`=`
View Solution`f(x)={(3x, 0lexle1),(-3x+5,1ltxle2):}` எனில்,
View Solution`f:RRrarrRR` என்பது `f(x)=lfloorx-3rfloor+|x-4|,x inRR`என வரையறுக்கப்பட்டால் `lim_(xrarr3^-)f(x)` ன் மதிப்பு
View Solution`lim_(xrarr0)(xe^x-sin x)/x`-ன் மதிப்பு
View Solution`lim_(xrarr0)(sin px)/(tan3x)=4` எனில் p-ன் மதிப்பு
View Solution`lim_(alphararrpi/4)(sinalpha-cosalpha)/(alpha-pi/4)`-ன் மதிப்பு
View Solution`lim_(nrarrinfty)(1/n^2+2/n^2+3/n^2+....+n/n^2)` -ன் மதிப்பு
View Solution`lim_(xrarr0) (e^sinx-1)/x=`
View Solution
EXERCISE questions and complete solutions for chapter வகை நுண்கணிதம் எல்லைகள் மற்றும் தொடர்ச்சித் தன்மை of SURA MATHS (TAMIL) of Class 11