கொடுக்கப்பட்ட மதிப்புகளை நிறைவு செய்யும் சார்பின் வரைபடம் வரைக. (i) f(0)வரையறுக்கப்படவில்லை limx→0f(x)=4f(2)=6limx→2f(x)=3 (ii) f(-2)=0 f(2)=0 limx→−2f(x)=0, limx→2f(x) என்ற எல்லை மதிப்பு இல்லை
Step by step video & image solution for கொடுக்கப்பட்ட மதிப்புகளை நிறைவு செய்யும் சார்பின் வரைபடம் வரைக. (i) f(0)வரையறுக்கப்படவில்லை lim_(xrarr0) f(x)=4f(2)=6lim_(xrarr2)f(x)=3 (ii) f(-2)=0 f(2)=0 lim_(xrarr-2) f(x)=0, lim_(xrarr2)f(x) என்ற எல்லை மதிப்பு இல்லை by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
கொடுக்கப்பட்டுள்ள கோணங்கள் எந்தக் காற்பகுதியில் அமையும் என்பதனை காண்க 25∘
View Solutionமுதல் கொள்கையினைப் பயன்படுத்திப் பின்வரும் சார்புகளின் வகைக்கெழுக்களைக் காண்க. (i) f(x)=6 (ii) f(x)=−4x+7 (iii) f(x)=x2+2
View Solutionlimx→0f(x)x2=1 find (i)limx→0f(x)(ii)limx→0f(x)x
View SolutionGiven lim_(x rarr0)(f(x))/(x^(2))=2 then lim_(x rarr0)[f(x)]=
View SolutionThe graph of y = f(x) is as shown in the following figure.

Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)
View Solutionयदि f एक निरंतर वर्धमान फलन है तब limx→0f(x2)−f(x)f(x)−f(0) का मान है :
View Solutionयदि f(x)=x2,x≥0
=x,x≤0
तो limx→0f(x)=
View Solutionlimx→2f(x) இங்கு f(x)={4−xx≠20x=2
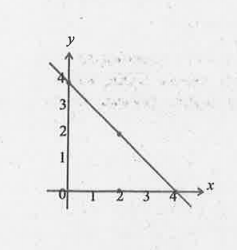
View SolutionLet f:R→R be a function satisfying Limx→0+f(x)=2, Limx→0−f(x)=3 and f(0)=4 The value of Limx→0f(x3−x2)Limx→0f(2x4−x5)=
View SolutionSketch the graph of a function f that satifies the given values:
f(0) is undefined limx→0f(x)=4, f(2)=6 , limx→2f(x)=3
View SolutionSketch the graph of a function f that satifies the given values:
f(−2)=0 ,f(2)=0, limx→−2f(x)=0 , limx→2f(x) does not exist.
View SolutionLet f:R→[0,∞) be such that limx→3f(x) exists and limx→3(f(x))2−4√|x−3|=0. Then limx→3f(x) equals
View SolutionThe graph of y = f(x) is as shown in the following figure.

Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)
View SolutionIf f(3)=2 thenlimx→2f(x2−1) = …........
View SolutionIf f(3)=2 thenlimx→2f(x2−1) = …........
View Solution
