Complete Solutions to Young'S Double Slit Experiment of chapter WAVE OPTICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | WAVE OPTICS |
| A2Z | Young'S Double Slit Experiment |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
In Young's double slit experiment, if one of the slit is closed fully, then in the interference pattern
View SolutionIn a Young's double slit experiment, the central point on the screen is
View SolutionIn Young's double slit experiment, if the two slits are illuminated with separate sources, no interference pattern is observed because
View SolutionIn Young's double slit experiment if monochromatic light is replaced by white light
View SolutionIn Young's experiment one slit is covered with a blue filter and the other (slit) with a yellow filter then the interference pattern
View SolutionIn Young’s double slit experiment, the central bright fringe can be identified
View SolutionIn Young's double slit experiment, the phase difference between the light waves reaching third bright fringe from the central fringe will be `(lambda=6000Å)`
View SolutionIn Young's double slit experiment, if the widths of the slits are in the ratio `4:9`, the ratio of the intensity at maxima to the intensity at minima will be
View SolutionIn a double slit experiment, instead of taking slits of equal widths, one slit is made twice as wide as the other. Then, in the interference pattern
View SolutionThe maximum intensity of fringes in Young's experiment is I. If one of the slit is closed, then the intensity at that place becomes `I_o`. Which of the following relation is true?
View SolutionIn a double slit experiment instead of taking slits of equal widths, one slit is made twice as wide as the other. Then, in the interference pattern
View SolutionIf a torch is used in place of monochromatic light in Young's experiment what will happen?
View SolutionIn Young's double slit experiment, a minimum is obtained when the phase difference of super imposing waves is
View SolutionThe slits in a Young's double slit experiemnt have equal width and the source is placed symmetrically with respect to the slits. The Intensty ast the central fringe is `I_0`. If one of the slits is closed, the intensit at this point will
View SolutionIn Young's double slit experiment, if the slit widths are in the ratio `1:9`, then the ratio of the intensity at minima to that at maxima will be
View SolutionTwo coherent sources of intensity ratio `1:4` produce an interference pattern. The fringe visibility will be
View SolutionIn Young's double slit experiment the amplitudes of two sources are `3a` and `a` respectively. The ratio of intensities of bright and dark fringes will be
View SolutionThe figure shows a double slit experiment with P and Q as the slits. The path lengths PX and QX are `nlambda` and `(n+2)lambda` respectively, where n is a whole number and `lambda` is the wavelength. Taking the central fringe as zero, what is formed at X?
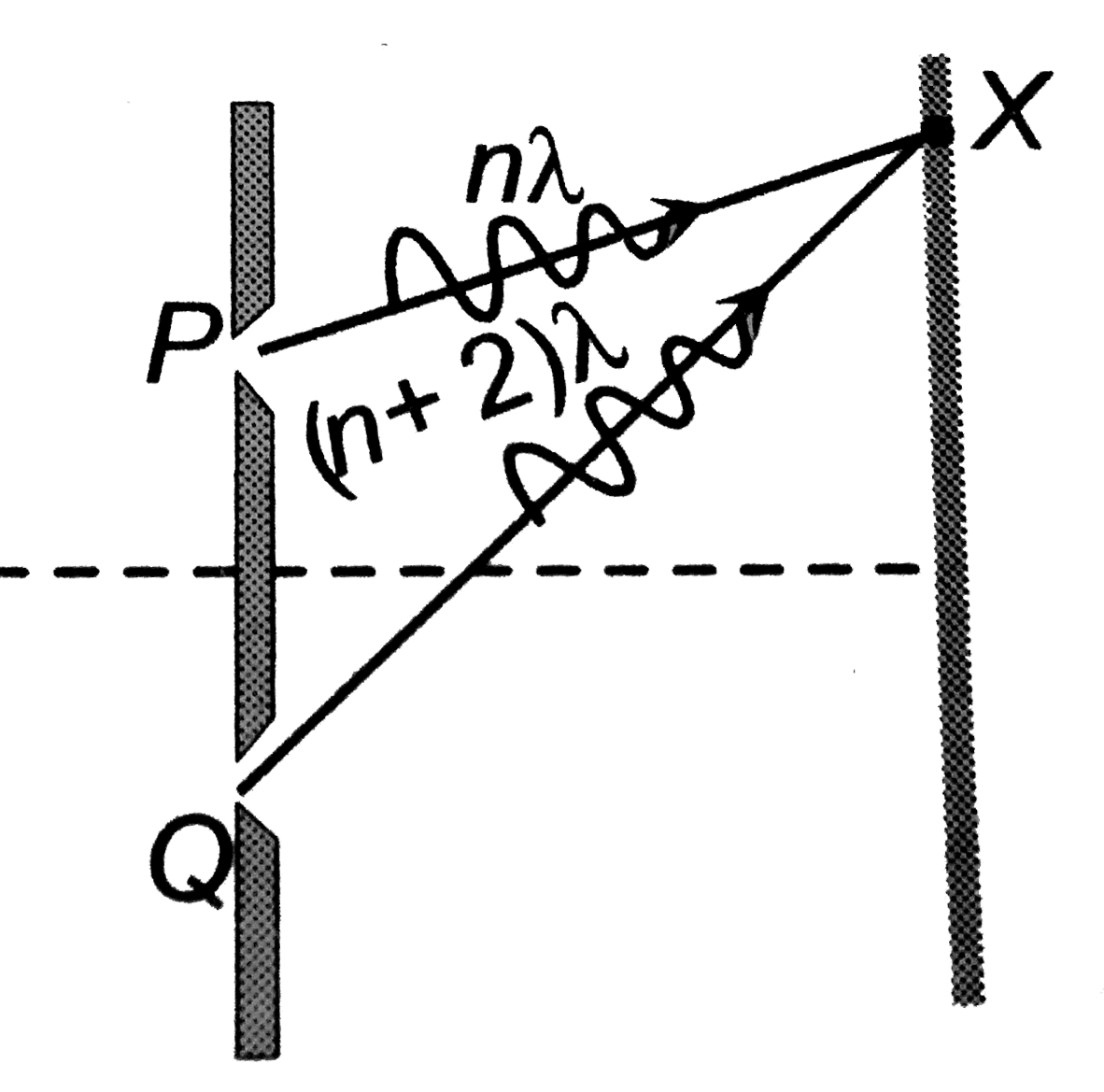
View SolutionIn Young's double slit experiment, when two light waves form third minimum, they have
View SolutionTwo slits at a distance of `1mm` are illuminated by a light of wavelength `6.5xx10^-7m`. The interference fringes are observed on a screen placed at a distance of `1m`. The distance between third dark fringe and fifth bright fringe will be
View SolutionIn the Young's double slit experiment with sodium light, the slits are `0.589m` apart. The angular separation of the third maximum from the central maximum will be (given `lambda=589mm`)
View SolutionIn Young's double slit experiment, an interference pattern is obtained on a screen by a light of wavelength `6000Å`, coming from the coherent sources `S_1` and `S_2`. At certain point P on the screen third dark fringe is formed. Then the path difference `S_1P-S_2P` in microns is
View SolutionIn Young's double slit experiment, the two slits acts as coherent sources of equal amplitude A and wavelength `lambda`. In another experiment with the same set up the two slits are of equal amplitude A and wavelength `lambda` but are incoherent. The ratio of the intensity of light at the mid-point of the screen in the first case to that in the second case is
View SolutionIn the Young's double slit experiment, if the phase difference between the two waves interfering at a point is `phi`, the intensity at that point can be expressed by the expression
View SolutionIn Young's double slit experiment, the intensity on the screen at a point where path difference is `lambda` is K. What will be the intensity at the point where path difference is `lambda//4`?
View SolutionIn Young's double slit interference experiment, the slit separation is made 3 fold. The fringe width becomes
View SolutionThe maximum number of possible interference maxima for slit-separation equal to twice the wavelength in Young's double-slit experiment is
View SolutionA Young's double slit experiment uses a monochromatic source. The shape of the interference fringes formed on a screen is
View SolutionIf `I_0` is the intensity of the principal maximum in the single slit diffraction pattern. Then what will be its intensity when the slit width is doubled?
View SolutionIn the set up shown in figure, the two slits `S_1` and `S_2` are not equidistant from the slit S. The central fringe at O is then
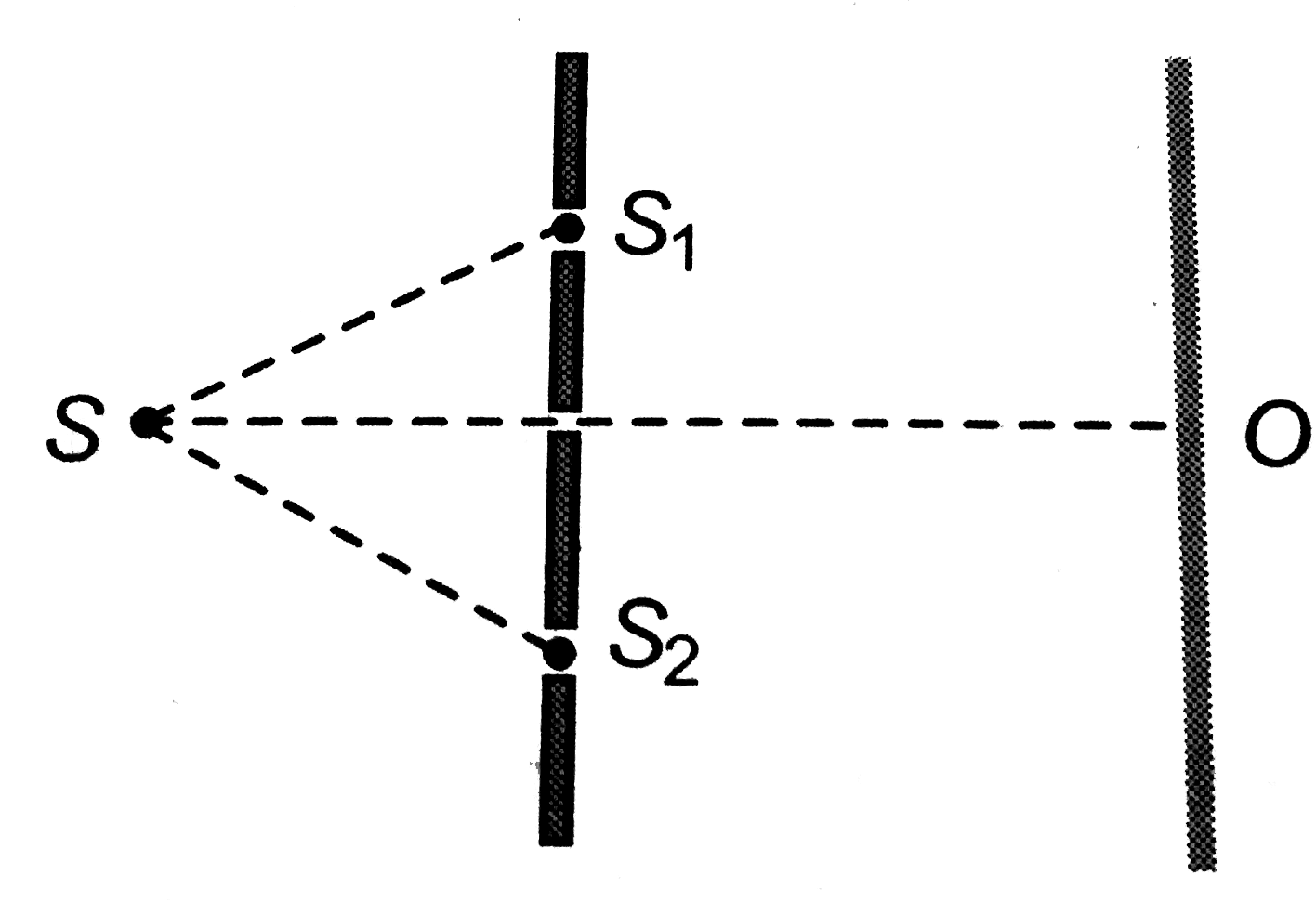
View SolutionA beam of light consisting of two wavelength `650nm` and `520nm` is used to illuminate the slit of a Young's double slit experiment. Then the order of the bright firnge of the longer wavelength that coincide with a bright fringe of the shorter wavelength at the least distance from the central maximum is
View SolutionTwo identical radiators have a separation of `d=lambda//4` where `lambda` is the wavelength of the waves emitted by either source. The initial phase difference between the sources is `lambda//4`. Then the intensity on the screen at a distant point situated at an angle `theta=30^@` from the radiators is (here `I_0` is intensity at that point due to one radiator alone)
View SolutionIn Young's double slit experiment, the 8th maximum with wavelength `lambda_1` is at a distance `d_1` from the central maximum and the 6th maximum with a wavelength `lambda_2` is at a distance `d_2`. Then `(d_1//d_2)` is equal to
View SolutionLight of wavelength `500nm` is used to form interference pattern in Young's double slit experiment. A uniform glass plate of refractive index `1.5` and thickness `0.1mm` is introduced in the path of one of the interfering beams. The number of fringes which will shift the cross wire due to this is
View SolutionTwo coherent sources of equal intensity produce maximum intensity of `100` units at a point. If the intensity of one of the sources is reduced by 36% reducing its width, then the intensity of light at the same point will be
View SolutionThe path difference between two interfering waves of equal intensities at a point on the screen is `lambda//4`. The ratio of intensity at this point and that at the central fringe will be
View SolutionIn a Young's double slit experiment, `I_0` is the intensity at the central maximum and `beta` is the fringe width. The intensity at a point P distant x from the centre will be
View SolutionTwo waves of equal amplitude and frequency interfere each other. The ratio of intensity when the two waves arrive in phase to that when they arrive `90^@` out of phase is
View SolutionIn Young's double slit experiment, we get `60` fringes in the field of view of monochromatic light of wavelength `4000Å`. If we use monochromatic light of wavelength `6000Å`, then the number of fringes obtained in the same field of view is
View SolutionIn a certain double slit experimental arrangement interference fringes of width `1.0mm` each are observed when light of wavelength `5000Å` is used. Keeping the set up unaltered, if the source is replaced by another source of wavelength `6000Å`, the fringe width will be
View SolutionTwo coherent light sources `S_1` and `S_2 (lambda=6000Å)` are `1mm` apart from each other. The screen is placed at a distance of `25cm` from the sources. The width of the fringes on the screen should be
View SolutionThe Young's experiment is performed with the lights of blue `(lambda=4360Å)` and green colour `(lambda=5460Å)`. If the distance of the 4th fringe from the centre is x, then
View SolutionIn two separate set-ups of the Young's double slit experiment, fringes of equal width are observed when lights of wavelength in the ratio of `1:2` are used. If the ratio of the slit separation in the two cases is `2:1`, the ratio of the distance between the plane of the slits and the screen in the two set-ups are
View SolutionIn double slit experiment, the angular width of the fringes is `0.20^@` for the sodium light `(lambda=5890Å)`. In order to increase the angular width of the fringes by `10%`, the necessary change in the wavelength is
View SolutionIn Young's double slit experiment, the slits are `0.5mm` apart and interference pattern is observed on a screen placed at a distance of `1.0m` from the plane containg the slits. If wavelength of the incident light is `6000Å`, then the separation between the third bright fringe and the central maxima is
View SolutionIn Young's double slit experiment, 62 fringes are seen in visible region for sodium light of wavelength `5893Å`. If violet light of wavelength `4358Å`, is used in place of sodium light, then number of fringes seen will be
View SolutionIn Young's double slit experiment, angular width of fringes is `0.20^@` for sodium light of wavelength `5890Å`. If complete system is dipped in water, then angular width of fringes becomes
View SolutionIn a Young's experiment, two coherent sources are placed `0.90mm` apart and the fringes are observed one metre away. If is produces the second dark fringe at a distance of `1mm` from the central fringe, the wavelength of monochromatic light used would be
View SolutionIn Young's experiement, the distance between slits is `0.28mm` and distance between slits and screen is `1.4m`. Distance between central bright fringe and third bright fringe is `0.9cm`. What is the wavelength of used light?
View SolutionTwo parallel slits `0.6mm` apart are illuminated by light source of wavelength `6000Å`. The distance between two consecutive dark fringe on a screen `1m` away from the slits is
View SolutionIf a transparent medium of refractive index `mu=1.5` and thickness `t=2.5xx10^-5m` is inserted in front of one of the slits of Young's Double Slit experiment, how much will be the shift in the interference patten? The distance between the slits is `0.5mm` and that between slits and screen is `100cm`
View SolutionIn a Young's double slit experiment, 12 fringes are observed to be formed in a certain segment of the screen when light of wavelength `600nm` is used. If the wavelength of light is changed to `400nm`, number of fringes observed in the same segment of the screen is given by
View SolutionIn a Young's double slit experiment, the slit separation is `1mm` and the screen is `1m` from the slit. For a monochromatic light of wavelength `500nm`, the distance of 3rd minima from the central maxima is
View SolutionIn a Young's double-slit experiment the fringe width is `0.2mm`. If the wavelength of light used is increased by 10% and the separation between the slits if also increased by 10%, the fringe width will be
View SolutionIn Young's double slit experiment, distance between two sources is 0.1mm. The distance of screen from the sources is 20cm. Wavelength of light used is `5460 Å`. Then, angular position of first dark fringe is approximately
View SolutionTwo slits are separated by a distance of `0.5mm` and illuminated with light of `lambda=6000Å`. If the screen is placed `2.5m` from the slits. The distance of the third bright image from the centre will be
View SolutionIn a two slit experiment with monochromatic light fringes are obtained on a screen placed at some distance from the sits. If the screen is moved by `5xx10^-2m` towards the slits the change in fringe width is `3xx10^-5m`. If separation between the slits is `10^-3m`, the wavelength of light used
View SolutionIn Young's double-slit experiment, the y-coordinate of central maxima and 10th maxima are 2 cm and 5 cm, respectively, When the YDSE apparatus is immersed in a liquid of refreactive index 1.5, the corresponding y-coordinates will be
View SolutionIn Young's double slit experiment how many maximas can be obtained on a screen (including the central maximum) on both sides of the central fringe if `lambda=2000Å` and `d=7000Å`
View SolutionIn a Young's double slit experiment, the slits are `2mm` apart and are illuminated with a mixture of two wavelength `lambda_0=750nm` and `lambda=900nm`. The minimum distance from the common central bright fringe on a screen `2m` from the slits where a bright fringe from one interference pattern coincides with a bright fringe from the other is
View SolutionThe ratio of the intensity at the centre of a bright fringe to the intensity at a point one-quarter of the distance between two fringe from the centre is
View SolutionIn Young's experiment, monochromatic light is used to illuminate the two slits A and B. Interference fringes are observed on a screen placed in front of the slits. Now if a thin glass plate is placed normally in the path of the beam coming from the slit
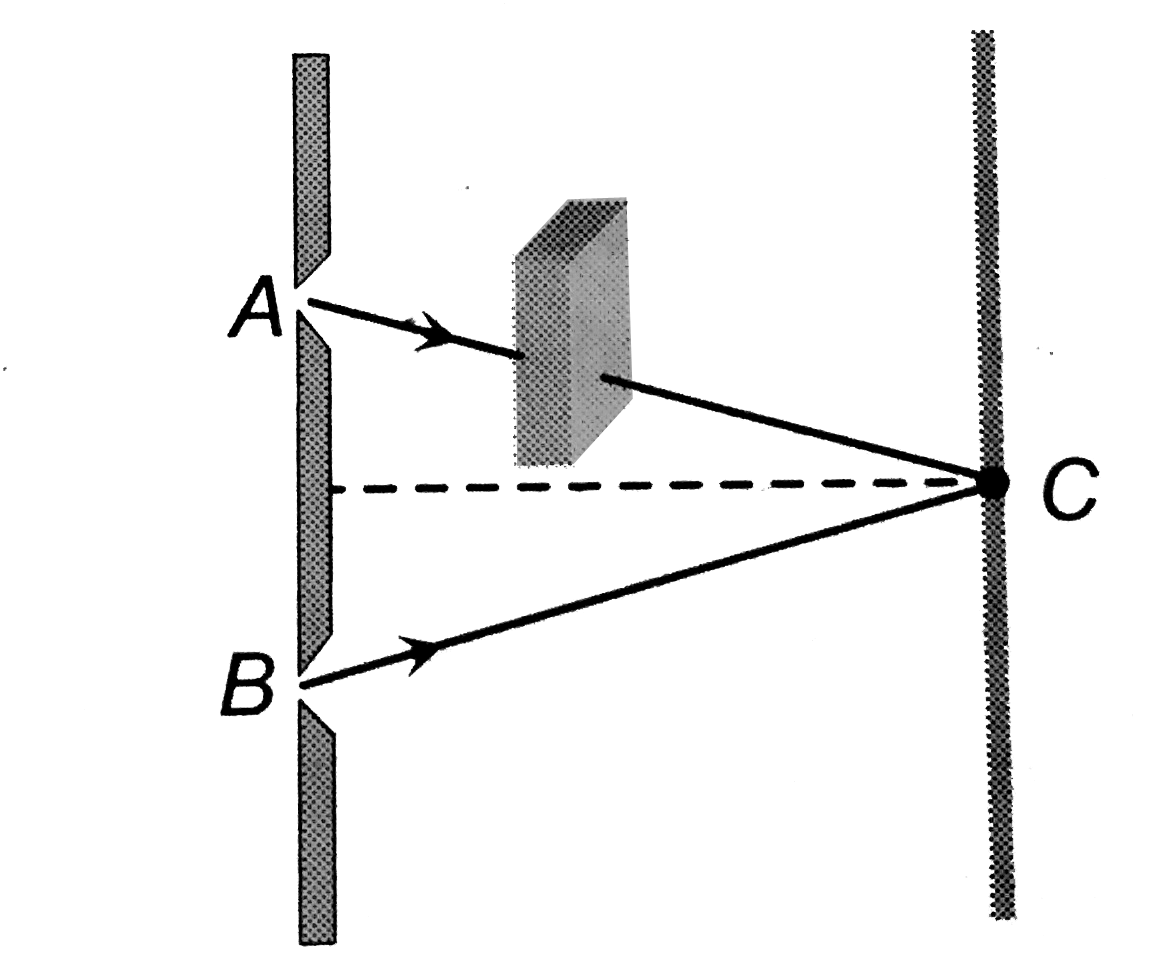
View SolutionA thin mica sheet of thickness `2xx10^-6m` and refractive index `(mu=1.5)` is introduced in the path of the first wave. The wavelength of the wave used is `5000Å`. The central bright maximum will shift
View SolutionA double slit experiment is performed with light of wavelength `500nm`. A thin film of thickness `2mum` and refractive index `1.5` is introduced in the path of the upper beam. The location of the central maximum will
View SolutionWhen one of the slits of Young's experiment is covered with a transparent sheet of thickness `4.8mm`, the central fringe shifts to a position originally occupied by the 30th bright fringe. What should be the thickness of the sheet if the central fringe has to shift to the position occupied by 20th bright fringe?
View SolutionA flake of glass (refractive index 1.5) is placed over one of the openings of a double slit apparatus. The interference pattern displaces itself through seven succesive maxima towards the side where the flake is placed. If wavelength of the diffracted light is `lambda=600nm`, then the thickness of
View SolutionIn the ideal double-slit experiment, when a glass-plate (refractive index 1.5) of thickness t is introduced in the path of one of the interfering beams (wavelength `lambda`), the intensity at the position where the central maximum occurred previously remains unchanged. The minimum thickness of the glass-plate is
View SolutionIn a Young's double slit experimental arrangement shown here, if a mica sheet of thickness t and refractive indec `mu` is placed in front of the slit `S_1`, then the path difference `(S_1P-S_2P)` is

View SolutionIn Young's double slit experiment, the fringes are displaced index 1.5 is introduced in the path of one of the beams. When this plate in replaced by another plate of the same thickness, the shift of fringes is `(3//2)x`. The refractive index of the second plate is
View SolutionIn a biprism experiement, by using light of wavelength `5000Å`, `5mm` wide fringes are obtained on a screen `1.0m` away from the coherent sources. The separation between the two coherent sources is
View SolutionIn Fresnel's biprism `(mu=1.5)` experiment the distance between source and biprism is `0.3m` and that between biprism and screen is `0.7m` and angle of prism is `1^@`. The fringe width with light of wavelength `6000Å` will be
View SolutionIf prism angle `alpha=1^@`, `mu=1.54`, distance between screen and prism `(b)=0.7m`, distance between prism and source `a=0.3m`, `lambda=180pi nm` then in Fresnel biprism find the value of `beta` (fringe width).
View SolutionIf Fresnel's biprism experiement as held in water in spite of air, then what will be the effect on fringe width?
View SolutionWhat is the effect on Fresnel's biprism experiment when the use of white light is made?
View SolutionIn Fresnel's biprism experiment, on increasing the prism angle, the fringe width will
View SolutionA double slit arrangement produces interference fringes for sodium light `(lambda=589nm)` that have an angular separation of `3.50xx10^-3` radian. For what wavelength would the angular separation be 10% greater?
View SolutionIn Young's double slit experiment, the intensity of light at a point on the screen where the path difference is `lambda=l`. The intensity of light at a point where the path difference becomes `lambda//3` is
View SolutionYellow light is used in single slit diffraction experiment with slit width `0.6mm`. If yellow light is replaced by X-rays then the pattern will reveal
View SolutionIn order to see diffraction the thickness of the film is
View SolutionA slit of width a is illuminated by white light. For red light `(lambda=6500Å)`, the first minima is obtained at `theta=30^@`. Then the value of a will be
View SolutionThe light of wavelength `6328Å` is incident on a slit of width `0.2mm` perpendicularly, the angular width of central maxima will be
View SolutionThe penetration of light into the region of geometrical shadow is called
View SolutionA slit of size `0.15m` is placed at `2.1m` from a screen. On illuminated it by a light of wavelength `5xx10^-5cm`. The width of central maxima will be
View SolutionA diffraction is obtained by using a beam of red light. What will happen if the red light is replaced by the blue light?
View SolutionWhat will be the angle of diffracting for the first minimum due to Fraunhofer diffraction with sources of light of wavelength `550nm` and slit of width `0.55mm`?
View SolutionAngular width `(beta)` of central maximum of a diffraction pattern on a single slit does not depend upon
View SolutionA single slit of width `0.20mm` is illuminated with light of wavelength `500nm`. The observing screen is placed `80cm` from the slit. The width of the central bright fringe will be
View SolutionIn Fresnel diffraction, if the distance between the disc and the screen is decreased, the intensity of central bright spot will
View SolutionA plane wavefront `(lambda=6xx10^-7m)` falls on a slit `0.4m` wide. A convex lens of focal length `0.8m` placed behind the slit focuses the light on a screen. What is the linear diameter of second maximum?
View SolutionRed light is generally used to observe diffraction pattern from single slit. If blue light is used instead of red light, then diffraction pattern
View SolutionConditions of diffraction is
View SolutionLight of wavelength `589.3nm` is incident normally on the slit of width `0.1mm`. What will be the angular width of the central diffraction maximum at a distance of `1m` from the slit?
View SolutionIn a diffraction pattern by a wire, on increasing diameter of wire, fringe width
View SolutionWhat will be the angular width of central maxima in Fraunhofer diffraction when light of wavelength `6000Å` is used and slit width is `12xx10^-5cm`?
View SolutionIf we observe the single slit Fraunhofer diffraction with wavelength `lambda` and slit width d, the width of the central maxima is `2theta`. On decreasing the slit width for the same `lambda`
View SolutionA beam of light of wavelength `600nm` from a distant source falls on a single slit `1mm` wide and the resulting diffraction pattern is observed on a screen `2m` away. The distance between the first dark fringes on either side of the central bright fringe is
View SolutionDirection of the first secondary maximum in the Fraunhofer diffraction pattern at a single slit is given by (a is the width of the slit)
View SolutionA parallel monochromatic beam of light is incident normally on a narrow slit. A diffraction patten is formed on a screen placed perpendicular to the direction of incident beam. At the first maximum of the diffraction pattern the phase difference between the rays coming from the edges of the slit is
View SolutionA light wave is incident normally over a slit of width `24xx10^-5cm`. The angular position of second dark fringe from the central maxima is `30^@`. What is the wavelength of light?
View SolutionA parallel beam of monochromatic light of wavelength `5000Å` is incident normally on a single narrow slit of width `0.001mm`. The light is focused by a convex lens on a screen placed on the focal plane. The first minimum will be formed for the angle of diffraction equal to
View Solution
Young'S Double Slit Experiment questions and complete solutions for chapter WAVE OPTICS of A2Z PHYSICS (HINGLISH) of Class 12