Complete Solutions to Problems Based On Mixed Concepts of chapter NUCLEAR PHYSICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | NUCLEAR PHYSICS |
| A2Z | Problems Based On Mixed Concepts |
| Number Of Questions | 58 |
| Academic Year | 2023-24 |
The binding energy per nucleon of `O^16` is `7.97 MeV` and that of `O^17` is `7.75 MeV`. The energy (in MeV) required to remove a neutron from `O^17` is.
View SolutionA heavy nucleus at rest breaks into two fragments which fly off with velocities in the ratio `8 : 1`. The ratio of radii of the fragments is.
View SolutionA star initially has `10^40` deuterons. It produces energy via the processes `._1H^2+_1H^2rarr_1H^3+p` and `._1H^2+_1H^3rarr_2He^4+n`. If the average power radiated by the star is `10^16` W, the deuteron supply of the star is exhausted in a time of the order of
(a) `10^6s` (b) `10^8s` (c) `10^12s`
The masses of the nuclei are as follows
`M(H^2)=2.014` amu, `M(n)=1.008` amu,
`M(p)=1.007` amu,`M(He^4)=4.001`amu
View SolutionIf `10%` of a radioactive material decays in `5` days, then the amount of original material left after `20` days is approximately.
View SolutionA radioactive isotope `X` with a half-life of `1.37 xx 109` years decays to `Y` which is stable. A sample of rock from the moon was found to contain both the elements `X` and `Y` which were in the ratio of `1 : 7`. The age of the rock is.
View SolutionThe half-life of radium is `1620 years` and its atomic weight is `226`. The number of atoms that will decay from its `1 g` sample per second will be .
View SolutionThe half-life period of a radioactive element x is same as the mean life time of another radioactive element y. Initially, both of them have the same number of atoms. Then,
(a) x and y have the same decay rate initially
(b) x and y decay at the same rate always
(c) y will decay at a faster rate than x
(d) x will decay at a faster rate than y
View SolutionFor a substance the average life for `alpha-`emission is `1620` years and for `beta-`emission is `405` years. After how much time the `1//4` of the material remains after `alpha` and `beta` emission ?
View SolutionThe half-life of radioactive Polonium `(Po)` is `138.6` days. For ten lakh Polonium atoms, the number of disintegrations in `24` hours is
View SolutionA radioactive nucleus undergoes `alpha-`emission to form a stable element. What will be the recoil velocity of the daughter nucleus is `V` is the velocity of `alpha`-emission and `A` is the atomic mass of radioactive nucleus ?
View SolutionHalf-life of a radioactive substance is `20` minutes. Difference between points of time when it is `33 %` disintegrated and `67 %` disintegrated is approximate.
View SolutionTwo radioactive `X_(1)` and `X_(2)` have decay constants `10 lambda ` and `lambda` respectively . If initially they have the same number of nuclei, then the ratio of the number of nuclei of `X_(1)` to that of `X_(2)`will be `1//e` after a time .
View Solution`A` and `B` are two radioactive substances whose half lives are `1` and `2` years respectively. Initially `10 gm` of `A` and `1 gm` of `B` is taken. The time (approximate) after which they will have same quantity remaining is.
View SolutionHalf life of a radio-active substance is `20` minutes. The time between `20 %` and `80 %` decay will be
View SolutionAfter `280` days, the activity of a radioactive sample is `6000` dps. The activity reduces to `3000` dps after another `140` days. The initial activity of the sample in dps is
View SolutionThe rate of disintegration was observed to be `1017` disintegrations per sec when its half life period is `1445` years. The original number of particles are.
View SolutionA small quantity of solution containing `Na^24` radio nuclide `(half-life=15 h)` of activity `1.0 microcurie` is injected into the blood of a person. A sample of the blood of volume `1cm^3` taken after `5h` shows an activity of `296` disintegrations per minute. Determine the total volume of the blood in the body of the person. Assume that the radioactive solution mixes uniformly in the blood of person.
(1 curie `=3.7 xx 10^10` disintegrations per second)
View SolutionA radioactive sample of `^(238)U` decay to Pb through a process for which the half is `4.5 xx 10^(9)` year. Find the ratio of number of nuclei of Pb to `^(238)U`after a time of `1.5 xx 10^(9)` year Given `(2)^(1//3)= 1.26`
View SolutionA radioactive sample is `alpha-`emitter with half life `138.6` days is observed by a student to have `2000` disintegration/sec. The number of radioactive nuclei for given activity are.
View SolutionA radioactive nucleus is being produced at a constant rate `alpha` per second. Its decay constant is `lamda`. If `N_0` are the number of nuclei at time `t = 0`, then maximum number of nuclei possible are.
View SolutionThe ratio of radii of nuclei `._13 A1^27` and `._52 X^A` is `3 : 5`. The number of neutrons in the nuclei of `X` will be
View SolutionIf one starts with one curie of radioactive substance `(T_(1//2) = 12 hrs)` the activity left after a period of `1` week will be about
View SolutionA nucleus `._ZX^A` emits `9 alpha-`particles and `5p` particle. The ratio of total protons and neutrons in the final nucleus is.
View SolutionThe nuclide `.^131 I` is radioactive, with a half-life of `8.04` days. At noon on January `1`, the activity of a certain sample is `60089`. The activity at noon on January `24` will be
View Solution`U^238` decays into `Th^234` by the emission of an a-particle. There follows a chain of further radioactive decays, either by `alpha`-decay or by `beta-`decay. Eventually a stable nuclide is reached and after that, no further radioactive decay is possible. which of the following stable nuclides is the end product of the `U^238` radioactive decay chain ?
View SolutionWhen a sample of solid lithium is placed in a flask of hydrogen gas then following reaction happened `._1^1 H + ._3 Li^7 rarr ._2 He^4 + ._2He^4`. This statement is.
 .
.
View SolutionConsider an initially pure `M gm` sample of `X`, an isotope that has a half-life of `T` hour, what is its initial decay rate (`N_A` = Avogadro No, atomic weight of `X` is `A`)
View SolutionAt a given instant there are `25 %` undecayed radioactive nuclei in a same. After `10 sec` the number of undecayed nuclei reduces to `6.25 %`, the mean life of the nuclei is.
View SolutionHighly energetic electrons are bombarded on a target of an element containing `30` neutrons. The ratio of radii of nucleus to that of Helium nucleus is `141//3`. The atomic number of nucleus will be.
View SolutionNumber of nuclei of a radioactive substance are `1000` and `900` at times `t=0` and time `t=2 s`. Then, number of nuclei at time `t=4s` will be
View SolutionWhich sample contains greater number of nuclei ?
a `5.00 -mu Ci` sample of `.^240 Pu` (half-life `6560 y`)
or `a 4.45-mu Ci` sample of `.^243 Am` (half-life `7370 y`).
View SolutionThe radioactivity of a given sample of whisky due to tritium (half life `12.3` years) was found to be only `3 %` of that measured in a recently purchased bottle marked `''7` years old''. The sample must have been prepared about.
View SolutionTransition between three energy energy levels in a particular atom give rise to three Spectral line of wevelength , in increasing magnitudes. `lambda_(1), lambda_(2)` and `lambda_(3)`. Which one of the following equations correctly ralates `lambda_(1), lambda_(2)` and `lambda_(3)`?
View SolutionSamples of two radioactive nuclides, `X` and `Y`, each have equal activity `A` at time `t=0`. X has a half-life of `24 years` and `Y` a half-life of `16 years`. The samples are mixed together. What will be the total activity of the mixture at `t=48` years?
View SolutionA stationery thorium nucleus `(A=200 , Z=90)` emits an alpha particle with kinetic energy `E_(alpha)`. What is the kinetic energy of the recoilling nucleus
View SolutionA hydrogen-like atom emits rediationof frequency `2.7 xx 10^(15)` Hz` when if makes a transition from `n = 2 to n = 1`. The frequency emitted in a transition from `n = 3 to n = 1` will be
View SolutionStationery nucleus `.^(238)U` decays by a emission generaring a total kinetic energy T:
`._(92)^(238) rarr ._(90)^(234)Th +._2^4 alpha`
What is the kinetic energy of the `alpha`-particle?
View SolutionThe ground (Fig.) shows the number of particles `Nt` emitted per second by a radioactive source as a function of time `t`
The relationship between `N_t` and `t` is.
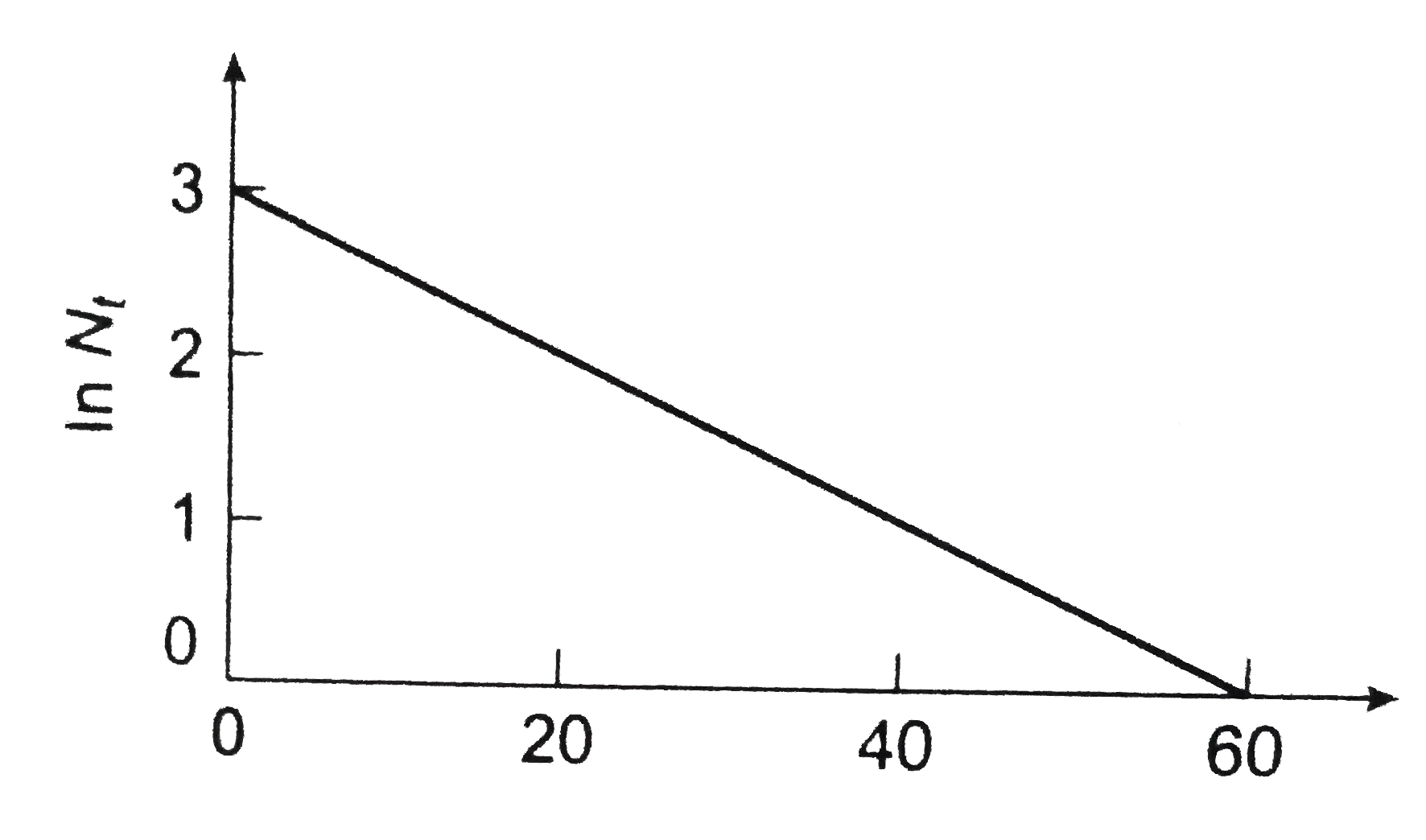 .
.
View SolutionThe activity of a radioative element decreases to one third of the original activity `I_(0)` in a period of nine years. After a further 1apse of nine years, its activity will be
View SolutionA radioactive element `A` with a half-value period of `2` hours decays giving a stable element `Y`. After a time `t` the ratio of `X` and `Y` atoms is `1 : 7` then `t` is :
View SolutionThe half-life period of RaB`(._(82)Pb^(214))` is `26.8 min`. The mass of one curie of RaB is
View SolutionThe count rate for `10 g` of radioactive material was measured at different times and this has been shown in the above graph with scale given. The half-life of the material and the total count in the first half-value period, respectively are.
View SolutionIf `10%` of a radioactive material decays in `5` days, then the amount of original material left after `20` days is approximately.
View SolutionA freshly prepared radioactive source of half life `2` hr emits radiation of intensity which is `64` times the permissible safe level . The minimum time after which it would be possible to work safely with this source is
View SolutionUranium ores contain one radium `-226` atom for every `2.8 xx 106` uranium `-238` atoms. Calculate the half-life of `._92 U6238` given that the half-life of `._88 Ra^226` is `1600` years `(._88Ra^226` is a decay product of `._92 U^238`) :
View SolutionThe radioactivity of a sample is `A_1` at time `t_1` and `A_2` at time `t_2` If the mean life of the specimen is `T`, the number of atoms that have disintegrated in the time interval of `(t_2 - t_1)` is :
View SolutionPlutinium has atomic mass `210` and a decay constant equal to `5.8 xx 10^(-8)s^(-1)`. The number of `alpha`-particles emitted per second by `1 mg `plutonium is
(Avagadro's constant =` 6.0 xx 10^(23)`).
View SolutionAt any instant, the ratio of the amounts of two radioactive substance is `2:1`. If their half-lives be, respectively, `12h` and `16h`, then after two days, what will be the ratio of the substances?
View SolutionThe radioactivity of a sample is `R_(1)` at a time `T_(1)` and `R_(2)` at time `T_(2)`. If the half-life of the specimen is T, the number of atoms that have disintegrated in the time `(T_(2) -T_(1))` is proporational to
View SolutionHalf-lives of two radioactive substances `A` and `B` are respectively `20` minutes and `40` minutes. Initially, he sample of `A` and `B` have equal number of nuclei. After `80` minutes the ratio of the remaining number of `A` and `B` nuclei is :
View SolutionA radioactive nucleus can decay by two differnet processess. The mean value period for the first process is `t_(1)` and that the second process is `t_(2)` .The effective mean value period for the two processes is .
View SolutionThe half-life of radium is `1620 years` and its atomic weight is `226`. The number of atoms that will decay from its `1 g` sample per second will be .
View SolutionWhat would be the energy required to dissociate completely `1 g` of `Ca-40` into its constituent, particles? Given: Mass of proton `=1.00866 am u`,
Mass of neutron `=1.00866 am u`,
Mass of `Ca-40 =39.97454 am u`, (Take `1 am u =931 MeV`).
View SolutionA star initially has `10^40` deuterons. It produces energy via the processes `._1^2H+_1^2Hrarr_1^3H+p` and `._1^2H+_1^3Hrarr_2^4He+n`, where the masses of the nuclei are
`m(.^2H)=2.014` amu, `m(p)=1.007` amu, `m(n)=1.008` amu and `m(.^4He)=4.001` amu. If the average power radiated by the star is `10^16 W`, the deuteron supply of the star is exhausted in a time of the order of
View SolutionIn the nuclear reaction `._1H^2 +._1H^2 rarr ._2He^3 +._0n^1` if the mass of the deuterium atom `=2.014741 am u`, mass of `._2He^3` atom `=3.016977 am u`, and mass of neutron `=1.008987 am u`, then the `Q` value of the reaction is nearly .
View SolutionIf mass of `U^(235)=235.12142 a.m.u.`, mass of `U^(236) =236.1205 amu`, and mass of neutron `=1.008665 am u`, then the energy required to remove one neutron from the nucleus of `U^(236)` is nearly about.
View SolutionThe binding energies per nucleon for deuteron (`._1H^2`) and helium (`._2He^4)` are `1.1 MeV` and `7.0 MeV` respectively. The energy released when two deutrons fuse to form a helium nucleus (`._2He^4`) is……..
View SolutionIn radioactive decay of a radioactive atom, its stability increases.
It is a spontaneous process.
View Solution
Problems Based On Mixed Concepts questions and complete solutions for chapter NUCLEAR PHYSICS of A2Z PHYSICS (HINGLISH) of Class 12