Complete Solutions to Radioactive Disintegration of chapter NUCLEAR PHYSICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | NUCLEAR PHYSICS |
| A2Z | Radioactive Disintegration |
| Number Of Questions | 65 |
| Academic Year | 2023-24 |
The graph between the instantaneous concentration (N) of a radioactive element and time (t) is.
View SolutionThe curve between the activity `A` of a radioactive sample and the number of active atoms `N` is.
View SolutionIn a radioactive substance at `t = 0`, the number of atoms is `8 xx 10^4`. Its half-life period is `3` years. The number of atoms `1 xx 10^4` will remain after interval.
View SolutionThe half-life period of radium is `1600` years. The fraction of a sample of radium that would remain after `6400` years is.
View SolutionThe percentage of quantity of a radioactive material that remains after 5 half-lives will be .
View SolutionThe radioactivity of a certain radioactive element drops to `1//64` of its initial value in `30` seconds. Its half-life is.
View SolutionThe average life `T` and the decay constant `lamda` of a radioactive nucleus are related as
View SolutionIf `T` is the half-life of a radioactive material, then the fraction that would remain after a time `(T)/(2)` is
View SolutionThe half-life of a radioactive element which has only `(1)/(32)` of its original mass left after a lapse of `60` days is
View SolutionThe life-life of `Bi^210` is `5` days. What time is taken by `(7//8)^th` part of the sample of decay ?
View SolutionA sample contains `16 gm` of radioactive material, the half-life of which is two days. After `32` days, the amount of radioactive material left in the sample is
View SolutionA radio-isotope has a half-life of `5` year. The fraction of the atoms of this material that would decay in `15` years will be
View SolutionThe half-life of pononium is `140` days. After how many days. `16 gm` polonium will be reduced to `1 gm` (or `15 gm` will decay) ?
View SolutionAn archaeologist analyses the wood in a phehistoric structure and finds that `C^14` (Half-life `= 5700` years) to `C^12` only one-fourth of that found in the cells buried plants. The age of the wood is about
View SolutionA radioactive element emits `200` particle per second. After three hours `25` particle per second are emitted. The half-life period of element will be
View SolutionThe half-life of the isotope `._11 Na^24` is `15` hrs. How much time does it take for `(7)/(8) th` of a sample of this isotope to decay ?
View SolutionIf `20 gm` of a radioactive substance due to radioactive decay reduces to `10 gm` in `4` minutes, then in what time `80 gm` of the same substance will reduce to `10 gm` ?
View SolutionA radioactive substance has a half life of `60` minutes. After `3` hours, the fraction of atom that have decayed would be.
View SolutionAfter two hours, one-sixteenth of the starting amount if a certain radioactive isotope remained undecayed . The half-life of the isotope is
View Solution`N` atoms of a radioactive element emit `n` alpha particles per second. The half-life of tge element is.
View SolutionThe half-life `(T)` and the disintegration constant `(lamda)` of a radioactive substance are related as
View SolutionThe half-life period of a radioactive substance is `5 min`. The amount of substance decayed in `20 min` will be
View SolutionRadon `(Ra)` decays into Polonium `(P_0)` by emitting an `alpha-`particle with half-life of `4` days. A sample contains `6.4 xx 10^10` atoms of `R_n`. After `12` days, the number of atoms of `R_n` left in the sample will be
View SolutionDecay constant of radiun is `lamda`. By a suitable process its compound radium bromide is obtained. The decay constant of radium bromide will be
View SolutionHalf-life of a radioactive substance` A` and `B` are, respectively, `20 min` and `40min`. Initially, the samples of `A` and `B` have equal number of nuclei. After `80 min`, the ratio of the remaining number of `A` and `B` nuclei is
View SolutionThe half - life of` `I ^ (131)` is 8 days. Given a sample of `I^(131)` at time `t = 0` , we can assert that
View SolutionCarbon `-14` decays with half-life of about `5, 800` years. In a sample of bone, the ratio of carbon `-14` to carbon `-12` is found to be `(1)/(4)` of what it is in free air. This bone may belong to a period about `x` centuries ago. Where `x` nearest to
View SolutionHalf-life of a radioacitve element is `10` days. The time during which quantity remains `1//10` of initial mass will be
View SolutionIf half-life of a radioactive element is `3` hours. After `9` hours its activity becomes
View SolutionAt any instant, the ratio of the amounts of two radioactive substance is `2:1`. If their half-lives be, respectively, `12h` and `16h`, then after two days, what will be the ratio of the substances?
View SolutionA ratio isotope has a half-life of `75` years. The fraction the atoms of this material that would decay in `150` years. Will be.
View SolutionThe activity of a radioactive sample is measured as `9750` counts per minute at `t = 0` and as `975` counts per minute at `t = 5` minutes. The decay constant is approximately
View SolutionThe acticity of a sample is `64 xx 10^-5 Ci`. Its half-life is `3` days. The activity will become `5 xx 10^-6 C i` after.
View SolutionThe half-life of radon is `3.8` days. Three forth of a radon sample decay in.
View Solution`3.8` days is the half-life period of a sample. After how many days. The sample will become `1//8 th ` of the original substance ?
View SolutionPlutonium decays with a half-life of `24000` years. If the plutonium is stored for `72000` years, then the fraction of plutonium that remains is.
View SolutionA radioactive substance has a half-life of `1` year. The fraction of this material, that would remain after `5` years will be.
View SolutionA radioactive sample has half-life of `5` years. Probability of decay in `10` years will be.
View SolutionIf half-life of a substance is `3.8` days and its quantity is `10.38 gm`. Then substance quantity remaining left after `19` days will be
View SolutionIn a mean life of a radioactive sample
View SolutionThree fourth of the active decays in a radioactive sample in `3//4 sec`. The half-life of the sample is
View SolutionDuring mean life of a radioactive element, the fraction that disintegrates is
View SolutionIf a radioactive substance reduces to `(1)/(16)` of its original mass in `40` days, what is its half-life ?
View Solution`99 %` of a radioactive element will decay between
View Solution`1 mg` gold undergoes decay with `2.7` days half-life period, amount left after `8.1` days is
View SolutionCeratain radioactive substance reduces to `25%` of its value is `16 days`. Its half-life is
View SolutionThe half-life of a radioactive substance against `alpha-`decay is `1.2 xx 10^7 s`. What is the decay rate for `4 xx 10^15` atoms of the substance ?
View Solution`10 gm` of radioactive material of half-life `15` year is kept in store for `20` years, The disintegrated material is.
View SolutionIn a sample of radioactive material, what percentage of the initial number of active nuclei will decay during one mean life ?
View SolutionA radioactive material has an initial amount `16 gm` After `120` days it reduces to `1 gm`. Then the half-life of radioactive material is
View SolutionHalf-life of a substance is `10` years. In what time, it becomes `(1)/(4) th` part of the initial amount ?
View SolutionIf `N_(0)` is the original mass of the substance of half - life period `t_(1//2) = 5 year` then the amount of substance left after `15` year is
View SolutionThe ratio activity of an element becomes `1//64 th` of its original value in `60 sec`. Then the half-life period is
View SolutionThe half-life of a radioactive substance is `48` hours. How much time will it take to disintegrate to its `(1)/(16) th` parts ?
View SolutionA radioactive substance has an average life of `5` hours. In a time of `5` hours
View SolutionA sample of a radioactive element has a mass of `10 g` at an instant `t=0`. The approxiamte mass of this element in the sample after two mean lives is .
View SolutionThe half-life of a sample of a radioactive substance is `1` hour. If `8 xx 10^10` atoms are present at `t = 0`, then the number of atoms decayed in the duration `t = 2` hour to `t = 4` hour will be
View SolutionA count rate meter shows a count of `240` per minute from a given radioactive source. One hour later the meter shows a count rate of `30` per minute. The half-life of the source is.
View SolutionActivity of radioactive element decreased to one third of original activity `R_0` in `9` years. After further `9` years, its activity will be
View SolutionThe half-life a radioacitve substance is `40` yeard. How long will it take to reduce to one fourth of its original amount and what is the value of decay constant ?
View SolutionA nucleus of mass `218` amu in Free State decays to emit an `alpha`-particle. Kinetic energy of the `beta-`particle emitted is `6.7 MeV`. The recoil energy (in MeV) of the daughter nucleus is
View SolutionRadioactive element decays to form a stable nuclide, then the rate of decay of reactant `((d N)/(d t))` will vary with time `(t)` as shown in figure.
View SolutionA radioactive sample has `N_0` active at `t = 0` . If the rate of disintegration at any time is `R` and the number of atoms is `N`, them the ratio `R//N` varies with time as.
View SolutionThe count rate of `10 g` of radioactive material was measured at different times and times has been shown in the figure. The half-life of material and the total counts (approximately) in the first half life period, respectively are.
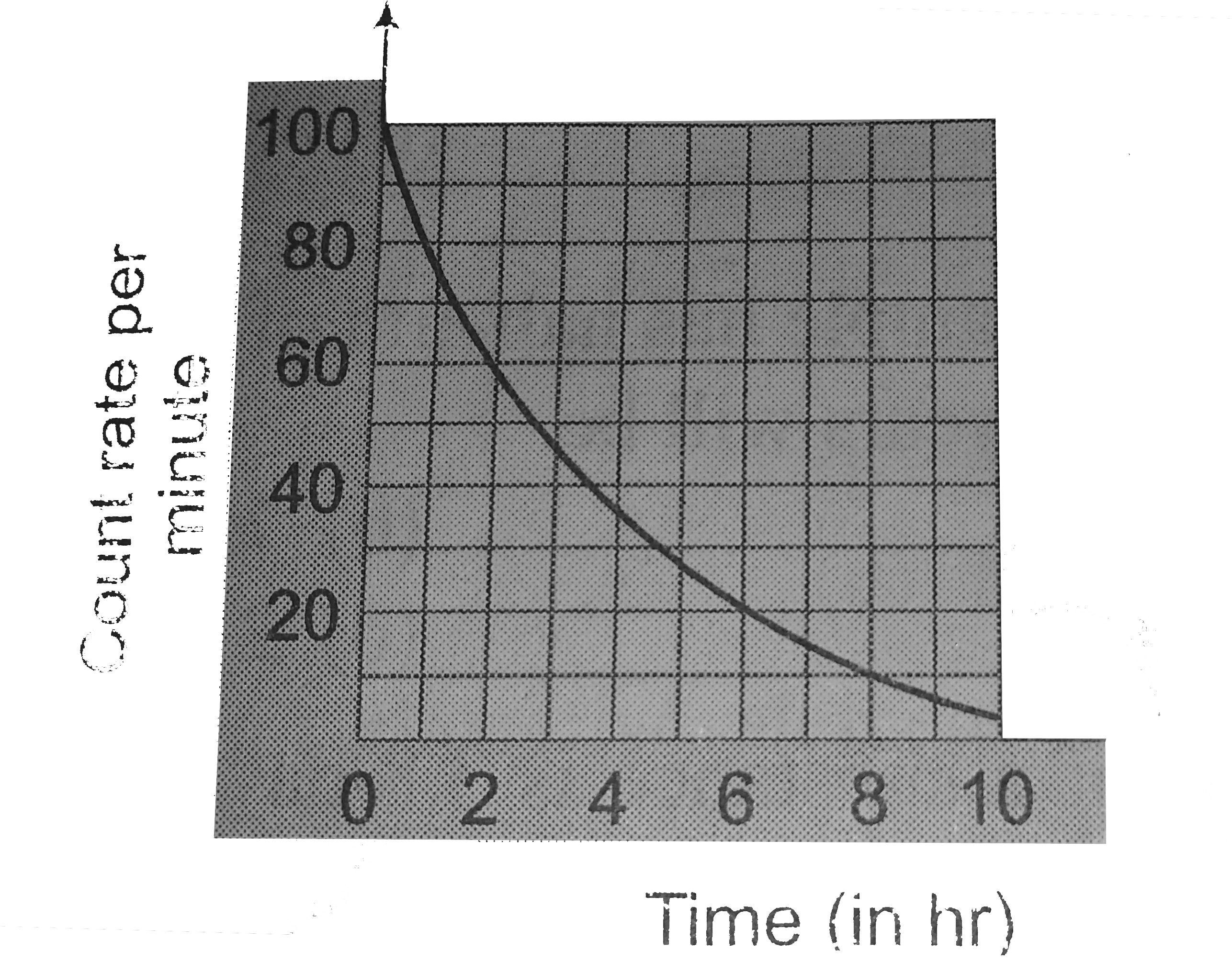 .
.
View SolutionThe fraction `f` of radioactive material that has decayed in time `t`, varies with time `t`. The correct variation id given by the curve.
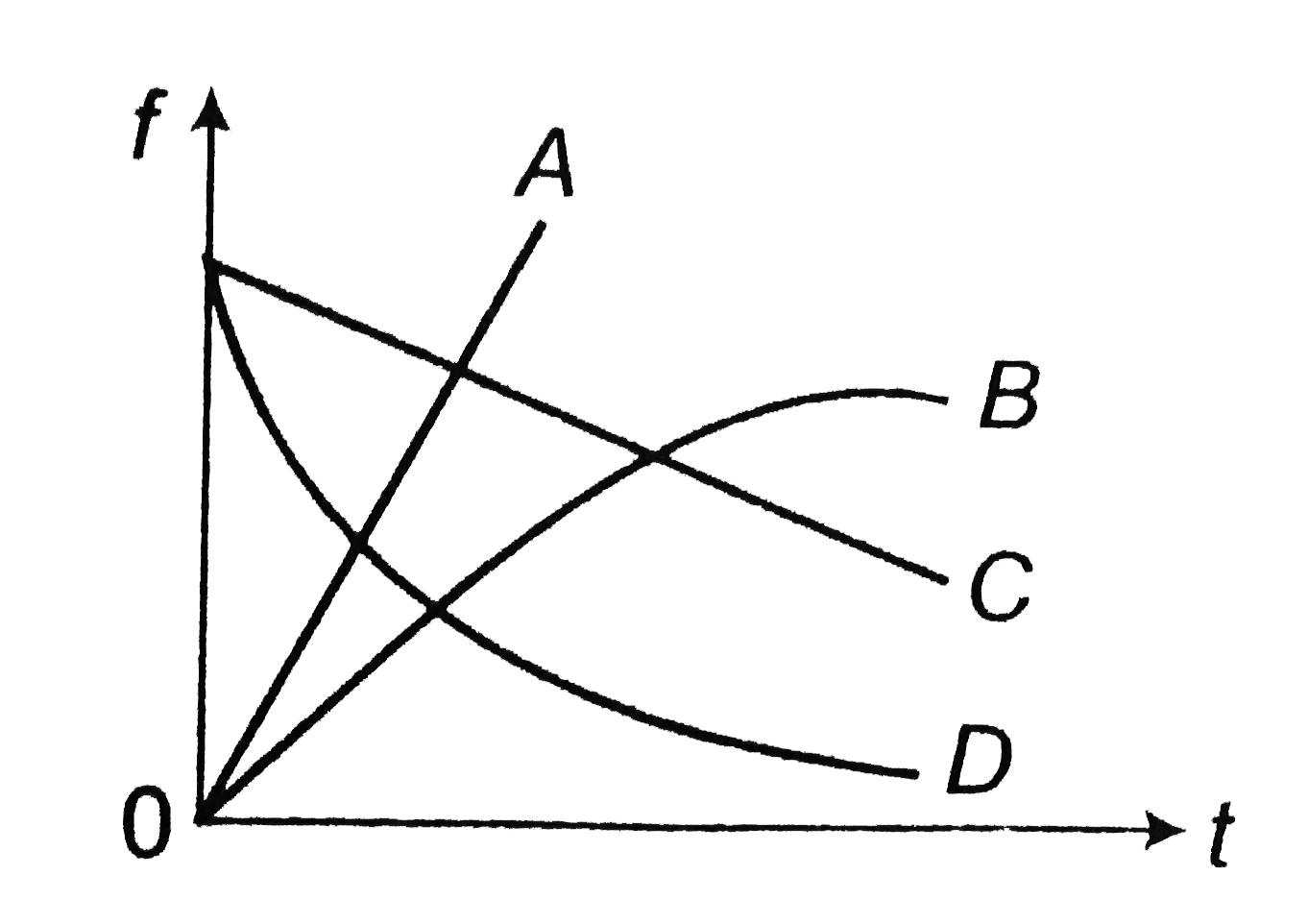 .
.
View Solution
Radioactive Disintegration questions and complete solutions for chapter NUCLEAR PHYSICS of A2Z PHYSICS (HINGLISH) of Class 12