Complete Solutions to ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS) of chapter GRAVITATION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | GRAVITATION |
| AAKASH INSTITUTE | ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS) |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
The acceleration due to gravity at a height 1 km above the earth is the same as at a depth d below the surface of earth. Then
View SolutionTwo astronauts are floating in gravitational free space after having lost contact with their spaceship. The two will
View SolutionStarting from the centre of the earth having radius R, the variation of `g` (acceleration due to gravity) is shown by
View SolutionA satellite of mass m is orbiting the earth (of radius R) at a height h from its surface. The total energy of the satellite in terms of `g_(0)`, the value of acceleration due to gravity at the earth's surface is
View SolutionAt what height from the surface of earth, the gravitation potential and the value of `g` are `-5.4 xx 10^(7) "J kg"^(-2) and 6 " ms"^(-2)` respecitvely ? Take, the radius of earth is 6400 km.
View SolutionThe ratio of escape velocity at earth `(V_(e))` to the escape velocity at a planet `(V_(p))` whose radius and mean density are twice as that of earth is
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small as comapred to the mass of the earth. Then,
View SolutionA remote-sensing satellite of earth revolves in a circular orbit at a height of `0.25xx10^(6)m` above the surface of earth. If earth's radius is `6.38xx10^(6)m` and `g=9.8ms^(-2)`, then the orbital speed of the satellite is
View SolutionKepler's third law states that square of period of revolution (T) of a planet around the sun, is proportional to third power of average distace r between the sun and planet i.e. `T^(2) = Kr^(3)`, here K is constant. If the masses of the sun and planet are M and m respectively, then as per Newton's law of gravitationa force of attraction between them is `F = (GMm)/(r^(2))`, hence G is gravitational constant. The relation between G and K is described as
View SolutionDependence of intensity of gravitational field (E) of the earth with distance (r) from centre of the earth is correctly represented by
View SolutionA body of mass `m` taken from the earth's surface to the height equal to twice the radius (R) of the earth. The change is potential energy of body will be
View SolutionInfinite number of bodies, each of mass 2 kg are situated on x-axis at distance 1 m, 2 m, 4 m, 8 m, respectively from the origin. The resulting gravitational potential due to this system at the origin will be
View SolutionA spherical planet has a mass `M_(p)` and `D_(p)`. A particle of mass m falling freely near the surface of this planet will experience an acceleration due to gravity, equal to
View SolutionA geostationary satellite is orbiting the earth at a height of 5R above that surface of the earth, R being the radius of the earth. The time period of another satellite in hours at a height of 2R from the surface of the earth is
View SolutionThe height at which the weight of a body becomes `1//6` th, its weight on the surface of the earth (radius R) is,
View SolutionIf `v_(e )` is escape velocity and `v_(o)` is orbital velocity of a satellite for orbit close to the earth's surface. Then these are related by
View SolutionWhich one of the following plots represents the variation of gravitational field F on a particle with distance r due to a thin spherical shell of radius R ?
( r is measured from the centre of the spherical shell )
View SolutionA planet moving along an elliptical orbit is closest to the sun at a distance `r_(1)` and farthest away at a distance of `r_(2)`. If `v_(1)` and `v_(2)` are the linear velocities at these points respectively, then the ratio `(v_(1))/(v_(2))` is
View SolutionA particle of mass M is situated at the centre of a spherical shell of same mass and radius R. The gravitational potential at a point situated at `(R )/(2)` distance from the centre will be
View SolutionA particle of mass m is thrown upwards from the surface of the earth, with a velocity u. The mass and the radius of the earth are respectively, M and R. G is gravitational constant and g is acceleration due to minimum value of u so that the particle does not return back to earth is :
View SolutionThe radii of circular orbits of two satellites A and B of the earth are 4R and R, respectively. If the speed of satellite A is 3v, then the speed of satellite B will be
View SolutionA particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance `a/2` from the centre.
View SolutionThe additional kinetic energy to be provided to a satellite of mass m revolving around a planet of mass M, to transfer it from a circular orbit of radius `R_(1)` to another of radius `R_(2)(R_(2) gt R_(1))` is
View SolutionThe dependence of acceleration due to gravity g on the distance r from the centre of the earth assumed to be a sphere of radius R of uniform density is as shown figure below.
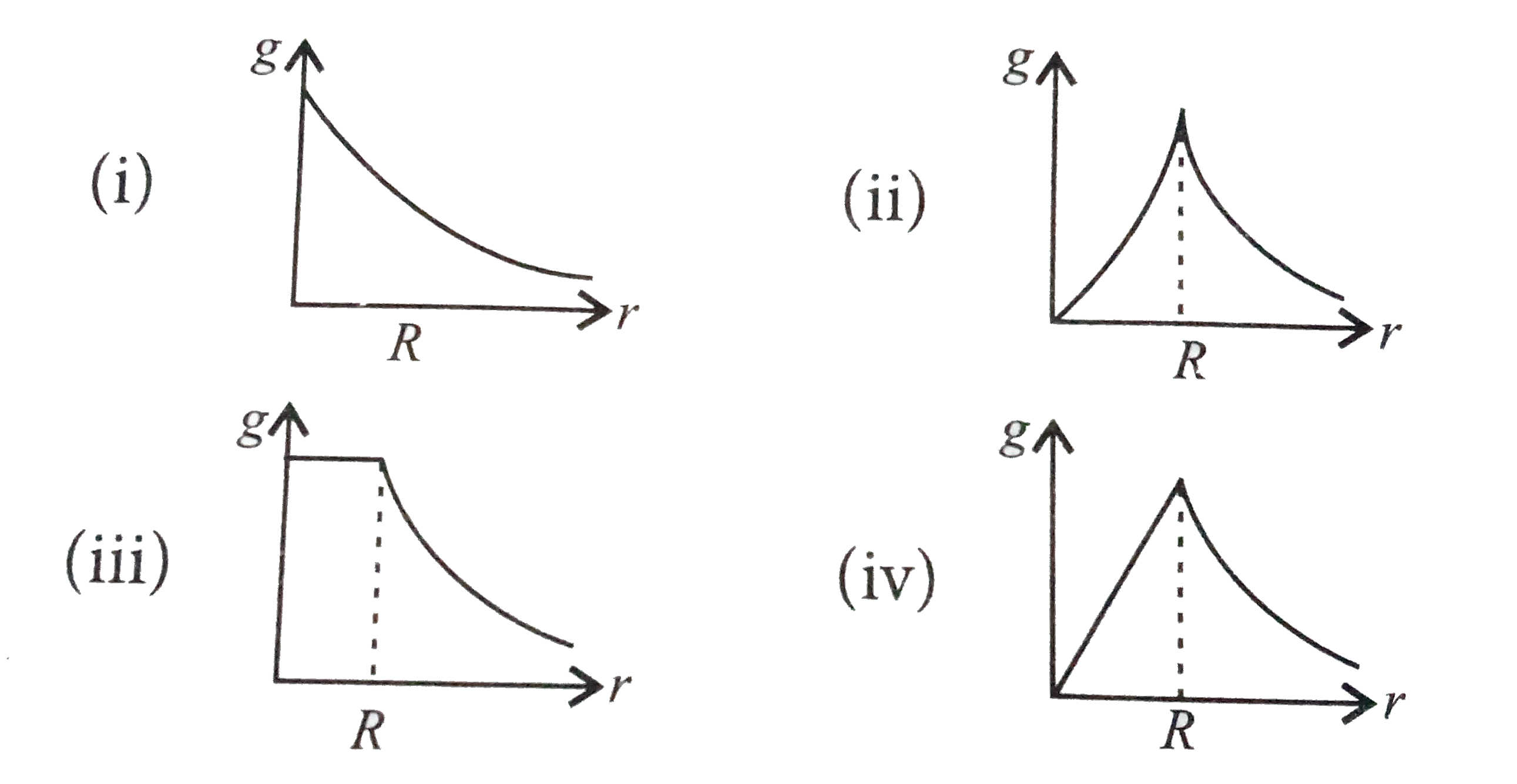
The correct figure is
View SolutionThe figure shows elliptical orbit of a planet m about the sun S. The shaded area SCD is twice the shaded area SAB. If `t_(1)` is the time for the planet to move from C to D and `t_(2)` is the time to move from A to B, then
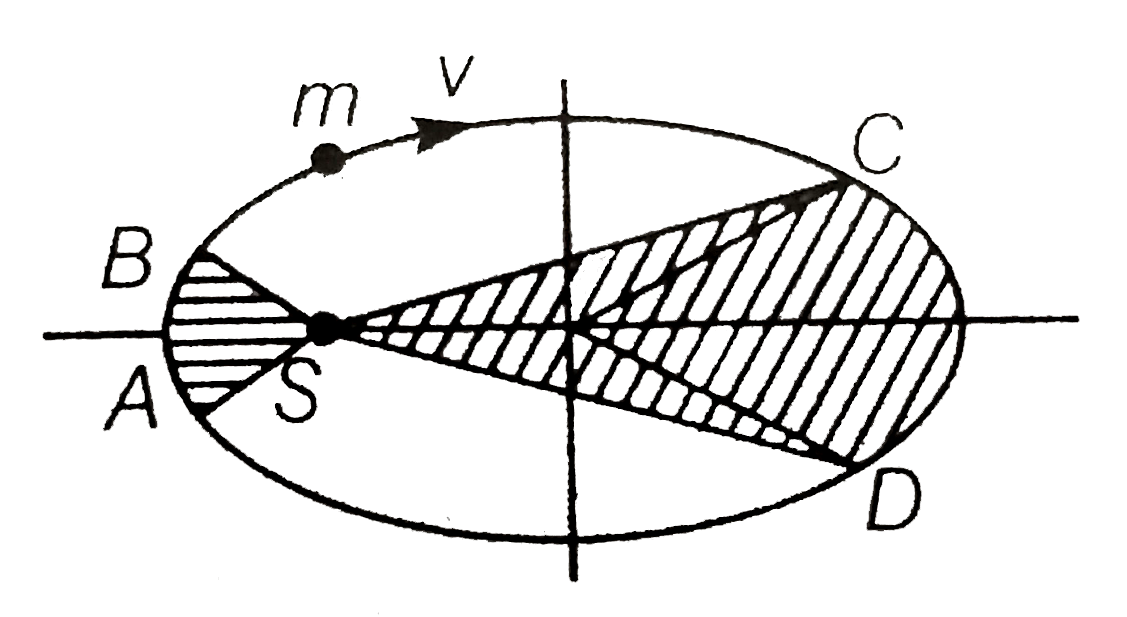
View SolutionTwo satellites of earth, `S_(1) and S_(2)` , are moving in the same orbit. The mass of `S_(1)` is four times the mass of `S_(2)` . Which one of the following statements is true ?
View SolutionThe earth is assumed to be a sphere of radius R. A platform is arranged at a height R from the surface of the earth. The escape velocity of a body from this platform is `fv_(e)`, where `v_(e)` is its escape velocity from the surface of the earth. Find the value of `f`.
View Solutionimagine a new planet having the same density as that of earth but it is 3 times bigger than the earth is size. If the acceleration due to gravity on the surface of earth is g and that on the surface of the new planet is g', then find the relation between g and g'.
View SolutionFor a satellite moving in an orbit around the earh, the ratio of kinetic energy to potential energy is
View SolutionThe radius of a planet is double that of earth but their average are the same. If the escape velocities at the planet and the earth are `v_(p)` and `v_( e)` respectively , then prove that `v_(p) = 2 v_(e)`.
View SolutionA particle of mass ‘m’ is kept at rest at a height 3R from the surface of earth, where ‘R’ is radius of earth and ‘M’ is mass of earth. The minimum speed with which it should be projected, so that it does not return back, is (g is acceleration due to gravity on the surface of earth)
View SolutionWhich of the following graphs shows the variation of acceleration due to gravity g with depth h from the surface of the earth ?
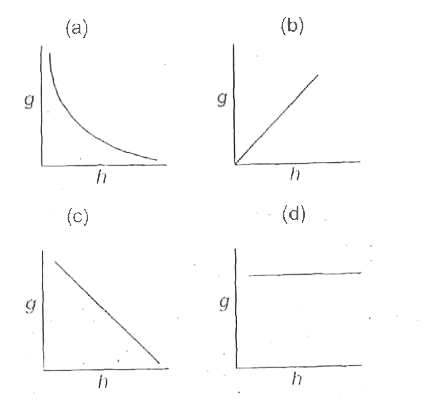
View SolutionAt what altitude (h) above the earth's surface would the accelration due to gravity be one fourth of its value at the earth's surface ?
View SolutionIf the gravitational force between two objects were proportional to `(1)/(R)` (and not as `(1)/(R^(2))`, where R is separation between them, then a particle in circular orbit under such a force would have its orbital speed v proportional to
View SolutionThe distance of two planets from the sun are `10^(13) and 10^(12)` m respectively. The ratio of the periods of the planet is
View SolutionThe radius of the earth is about `6400 km` and that of is about `3200 km`. The mass of the earth is about `10` times the mass of Mars. An object weighs `200 N` the surface of the earth. Its weight on the surface of mars would be
View SolutionThe earth `(mass = 10^(24) kg)` revolves round the Sun with an angular velocity `2 xx 10^(-7) rad s^(-1)` in a circular orbit of radius `1.5 xx 10^(8)km`. Find the force exerted by the Sun on the earth (in `xx 10^(21)N)`.
View SolutionTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of each particle is
View SolutionThe acceleration due to gravity g and density of the earth `rho` are related by which of the following relations?
(Where G is the gravitational constant and `R_(E)` is the radius of the earth )
View SolutionWhat will be the formula of the mass in terms of g,R and G ? (R = radius of the earth)
View SolutionThe time of revolution of planet `A` round the sun is `8` times that of another planet `B`. The distance of planet `A` from the sun is how many times the distance of `B` from the sun
View SolutionThe escape velocity of a body on the surface of the earth is `11.2km//s`. If the earth's mass increases to twice its present value and the radius of the earth becomeshalf, the escape velocity would become
View SolutionThe escape velocity of a sphere of mass m is given by (G= univesal gravitational constant, `M_(e) =` mass of the earth and `R_(e) =` radius of the earth)
View SolutionA body of weight 72 N moves from the surface of earth at a height half of the radius of earth , then geavitational force exerted on it will be
View SolutionA planet has mass equal to mass of the earth but radius one fourth of radius of the earth . Then escape velocity at the surface of this planet will be
View SolutionWith what velocity should a particle be projected so that its maximum height attained becomes equal to radius of earth ?
View SolutionA body of mass m is placed on the earth's surface. It is then taken from the earth's surface to a height ` = 3R`, then the change in gravitational potential energy is
View SolutionThe acceleration due to gravity on the planet A is 9 times the acceleration due to gravity on the planet B. A man jumps to a height of 2m on the surface of A. what is the height of jump by the same person on the planet B ?
View SolutionTwo spheres of masses m and M are situated in air and the gravitational force between them is F. the space around the masses is now filled with a liquid of specific gravity 3. The gravitational force will now be
View SolutionThe density of newly discovered planet is twice that of the earth. The acceleration due to gravity at the surface of the planet is equal to that at the surface of the earth. If the radius of the earth is R, the radius of the planet would be
View SolutionA ball is dropped from a satellite revolving around the earth at a height of 120km. The ball will
View Solution
ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS) questions and complete solutions for chapter GRAVITATION of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS GRAVITATION
- ASSIGNMENT SECTION -A (Objective Type Questions (one option is correct))
- ASSIGNMENT SECTION -B (Objective Type Questions (one option is correct))
- ASSIGNMENT SECTION -C (Objective Type Questions (More than one option are correct))
- ASSIGNMENT SECTION -D (Linked Comprehension Type Questions)
- ASSIGNMENT SECTION -E (Assertion - Reason Type Questions)
- ASSIGNMENT SECTION -F (Matrix - Match Type Questions)
- ASSIGNMENT SECTION -G (Integer Answer Type Questions)
- ASSIGNMENT SECTION -H (Multiple True - False Type Questions)
- ASSIGNMENT SECTION -I (Subjective Type Question)
- ASSIGNMENT SECTION -J (Aakash Challengers Questions)
- ASSIGNMENT SECTION - A (OBJECTIVE TYPE QUESTIONS)
- ASSIGNMENT SECTION - B (OBJECTIVE TYPE QUESTIONS)
- ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS)
- ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
- Example
- EXERCISE
- TRY YOUR SELF
- Try Yourself