Complete Solutions to Example of chapter GRAVITATION of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | GRAVITATION |
| AAKASH INSTITUTE | Example |
| Number Of Questions | 48 |
| Academic Year | 2023-24 |
The distance of two planets from the sun are `10^(13) and 10^(12)` m respectively. The ratio of the periods of the planet is
View SolutionA geostationary satellite is orbiting the earth at a height of 6R above the surface of the earth, where R is the radius of the earth. The time period of another satellite at a height of 2.5 R from the surface of the earth is …… hours.
View SolutionIf the masses of two bodies are quadrupled and the distance between their centres is doubled, then how many times the force of gravitation between them will be changed ?
View SolutionIf the distance between the two bodies is increased to two times, then by how many times the mass of one of the bodies to be changed to maintain the same gravitational force ?
View SolutionThree equal masses of `m kg` each are fixed at the vertices of an equilateral triangle `ABC`.
a. What is the force acting on a mass `2m` placed at the centroid `G` of the triangle?
b. What is the force if the mass at the vertex `A` is doubled? Take `AG=BG=CG=1m`
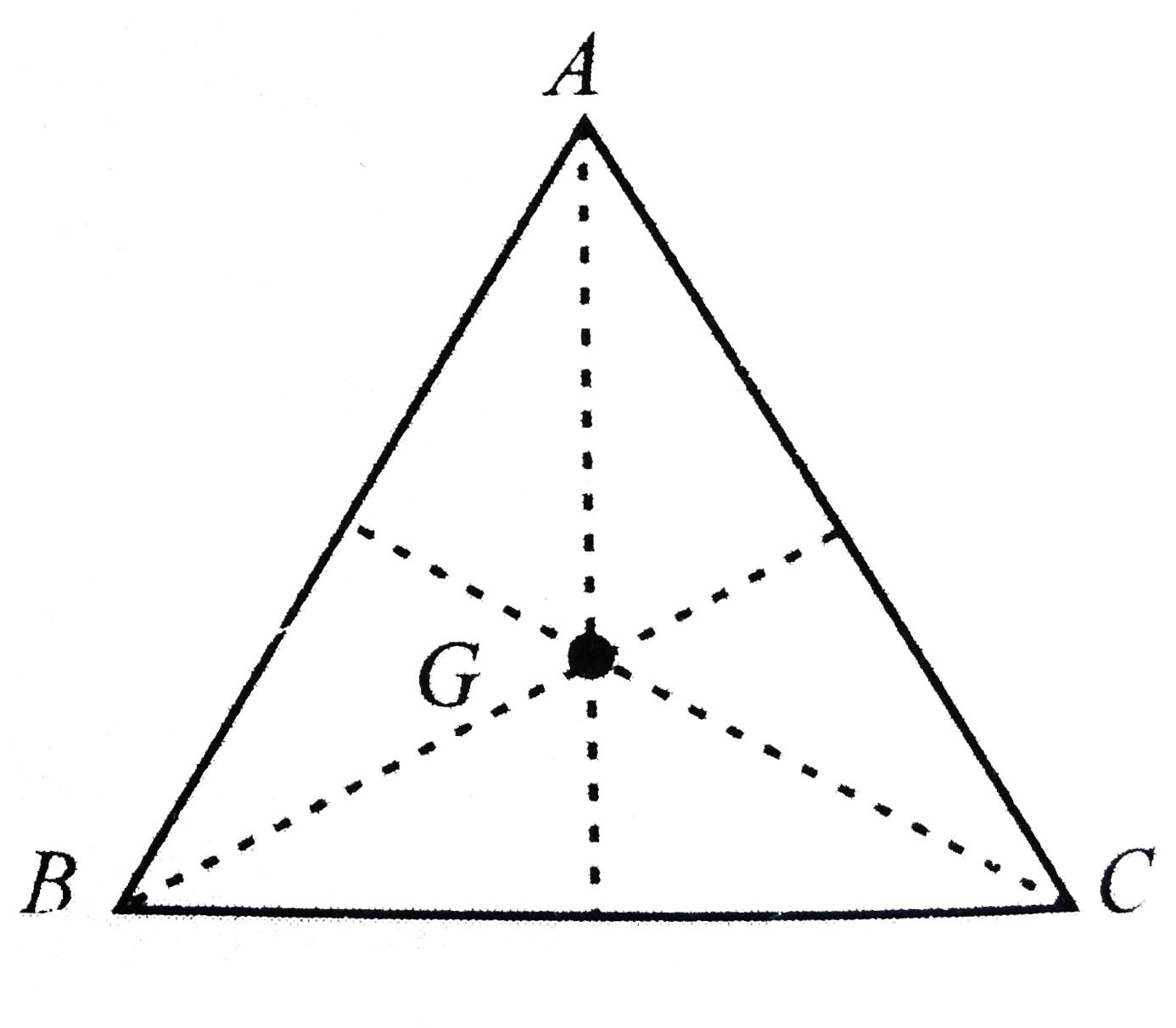
View SolutionThree balls each of mass 0.5 kg are kept at the vertices of an isosceles right triangle with its hypotenuse of `2sqrt(2)` m. What will be the net gravitational force on the ball kept at the vertex of right angle ?
View SolutionTwo bodies A and B having masses M and 3M respectively are kept at a distance 2.73 m apart. A small particle of mass m is to be place so that the net gravitational force on it, due to A and B is zero. What will be its distance from body A ?
View SolutionWhat will be the relation the acceleration due to gravity on the surface of the earth and on a planet respectively, whose mass and radius are twice that of the earth ?
View SolutionA spherical planet far out in space has a mass `M_(0)` and diameter `D_(0)`. A particle of mass m falling freely near the surface of this planet will experience an accelertion due to gravity which is equal to
View SolutionAt what altitude, the acceleration due to gravity reduces to half of its value as that on the surface of the earth ? Take radius of earth as `6.410^(6)` m, g on the surface of the earth as `9.8 m//s^(2)`.
View SolutionAt what height the acceleration due to gravity decreases by 36% of its value on the surface of the earth ?
View SolutionAt what depth the acceleration due to gravity becomes zero ?
View SolutionAt what depth from the surface of the earth, the acceleration due to gravity will be `(1)/(4)` th the value of g on the surface of the eath ?
View SolutionFind the potential energy of a system of four particles each of mass 2m kept at the vertices of a square of side x. Also find the potential at the centr of the square.
View SolutionTwo heavy spheres of masses `10^(4)` kg and `10^(6)` kg and each of radius 20 cm are separated by a distance of 100 m. What will be the potential at the mid-point of the joining their centres ?
View SolutionThe ratio of the masses and radii of two planets are 2 : 3 and 4 : 9. What is the ratio of the escape speed at their surface ?
View SolutionWhat will be the escape speed from a planet having mass 8 times that of earth and diameter 4 times that of the earth ? `[v_(e)=11.2 km//s]`
View SolutionThe value of escape speed from certain planet is 4 km/s. What will be the orbital speed of a satellite orbiting close to its surface ?
View SolutionWhat will be the orbital speed from a planet of mass `10^(30)` kg and and of radius `10^(8)` m ?
View SolutionWhat will be the mass of an object under free fall, if at earth's surface it weighs 100 N ? [Take `g=10 m//s^(2)`]
View SolutionA particle of mass 1 kg is released from rest at a point where gravitational potential is 5 J/kg. After some time, it passes through a point B with a speed of 1 m/s. What is the gravitational potential at B ?
View SolutionThe gravitational field due to a mass distribution is given by `vec(l)=(k)/(x^(2))hat(i)`, where k is a constant. Assuming the potential to be zero at infinity, find the potential at a point x = a.
View SolutionThe gravitational potential due to a mass distrubution is given by `V=(8x)/(x^(2)+p^(2))`. Find gravitational field at x = p.
View SolutionThe gravitational field due to a mass distribution is given by `l=kx^(-3//2)` in x-direction, where k is a positive constant. Taking potential to be zero at infinity, find its value at a distance x.
View SolutionThe distance of two planets from the sun are `10^(13) and 10^(12)` m respectively. The ratio of the periods of the planet is
View SolutionA satellite of time period 24 h is orbiting the earth at a height 6R above the surface of earth, where R is radius of earth. What will be the time period of another satellite at a height 2.5 R from the surface of earth ?
View SolutionIf the masses of two bodies are quadrupled and the distance between their centers is doubled, then how many times the force of gravitation between them will be changed ?
View SolutionIf the distance between the two spherical bodies is increased to four times, then by how many times, the mass of one of the bodies to be changed to maintain the same gravitational force ?
View SolutionThree equal masses of m kg each are fixed at the vertices of an equilateral triangle ABC.
(a) What is the force acting on a mass 2m placed at the centroid G of the triangle?
(b) What is the force if the mass at the vertex A is doubled?
Take AG=BG=CG=1m (see Fig.8.5)
View SolutionTwo particles of equal mass `m_(0)` are moving round a circle of radius r due to their mutual gravitational interaction. Find the time period of each particle.
View SolutionTwo particles A and B having masses M and 4M respectively are kept at a distance 2.73 m apart. Another small particle of mass m is to be placed so that the net gravitational force on it is zero. What will be its distance from body A ?
View SolutionA particle of mass `m` is situated at a distance `d` from one end of a rod of mass `M` and length `L` as shown in diagram. Find the magnitude of the gravitational force between them

View Solution`g_(e)` and `g_(p)` denote the acceleration due to gravity on the surface of the earth and another planet whose mass and radius are twice as that of earth. Then
View SolutionA spherical planet has a mass `M_(p)` and `D_(p)`. A particle of mass m falling freely near the surface of this planet will experience an acceleration due to gravity, equal to
View SolutionAt what altitude, the acceleration due to gravity reduces to one fourth of its value as that on the surface of the earth ? Take radius of earth as `6.4 xx 10^(6) m`, g on the surface of the earth as `9.8 ms^(-2)`.
View SolutionAt what height the acceleration due to gravity decreases by 36% of its value on the surface of the earth ?
View SolutionAt what depth the acceleration due to gravity becomes zero ?
View SolutionAt what depth from the surface of the earth, the acceleration due to gravity will be `(1)/(4)` th the value of g on the surface of the earth ?
View SolutionAt what rate should the earth rotate so that the apparent g at the equator becomes zero? What will be the length of the day in this situation?
View SolutionA particle is projected vertically with speed V from the surface of the earth . Maximum height attained by the particle , in term of the radius of earth R,V and g is ( V `lt` escape velocity , g is the acceleration due to gravity on the surface of the earth )
View SolutionAn object is dropped from height `h=2 R` on the surface of earth. Find the speed with which it will collide with ground by neglecting effect of air. (Where R is radius of earth, take mass of earth M)
View SolutionThree particles of mass m, 2m and 4m are placed at the corner of an equilibrium triangle of side a, Calculate :
(a) The potential energy of the system
(ii) The work done on the sysem if the side of the triangle is changed from a to 2a. Assume the potential energy to be zero when the separation is infinity.
View SolutionTwo heavy spheres of masses `10^(4)` kg and `10^(6)` kg and each of radius 20 cm are separated by a distance of 100 m. What will be the potential at the mid-point of the joining their centres ?
View SolutionThe ratio of the masses and radii of two planets are 2 : 3 and 4 : 9. What is the ratio of the escape speed at their surface ?
View SolutionWhat will be the escape speed from a planet having mass 8 times that of earth and diameter 4 times that of the earth ? `[v_(e)=11.2 km//s]`
View SolutionThe value of escape speed from certain planet is 4 km/s. What will be the orbital speed of a satellite orbiting close to its surface ?
View SolutionAssume that the force of gravitation `F prop 1/(r^(n))` . Then show that the orbital speed in a circular orbit of radius r is proportional to ` 1/(r^((n-1)//2))` , while its period T is proportional to ` r^((n+1)//2)`
View SolutionWhat will be the mass of an object under free fall, if at earth's surface it weighs 100 N ? [Take `g=10 m//s^(2)`]
View Solution
Example questions and complete solutions for chapter GRAVITATION of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS GRAVITATION
- ASSIGNMENT SECTION -A (Objective Type Questions (one option is correct))
- ASSIGNMENT SECTION -B (Objective Type Questions (one option is correct))
- ASSIGNMENT SECTION -C (Objective Type Questions (More than one option are correct))
- ASSIGNMENT SECTION -D (Linked Comprehension Type Questions)
- ASSIGNMENT SECTION -E (Assertion - Reason Type Questions)
- ASSIGNMENT SECTION -F (Matrix - Match Type Questions)
- ASSIGNMENT SECTION -G (Integer Answer Type Questions)
- ASSIGNMENT SECTION -H (Multiple True - False Type Questions)
- ASSIGNMENT SECTION -I (Subjective Type Question)
- ASSIGNMENT SECTION -J (Aakash Challengers Questions)
- ASSIGNMENT SECTION - A (OBJECTIVE TYPE QUESTIONS)
- ASSIGNMENT SECTION - B (OBJECTIVE TYPE QUESTIONS)
- ASSIGNMENT SECTION - C (PREVIOUS YEARS QUESTIONS)
- ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
- Example
- EXERCISE
- TRY YOUR SELF
- Try Yourself