Complete Solutions to ASSIGNMENT (SECTION -C) (Previous Year Questions) of chapter THERMODYNAMICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | THERMODYNAMICS |
| AAKASH INSTITUTE | ASSIGNMENT (SECTION -C) (Previous Year Questions) |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
A Carnot engine, having an efficiency of `eta= 1/10` as heat engine, is used as a refrigerator. If the work done on the system is 10 J, the amount of energy absorbed from the reservoir at lower temperature is
View SolutionThermodynamic processes are indicated in the following diagram

Match the following :

View SolutionOne mole of an ideal monatomic gas undergoes a process descrbed by the equation `pV^(3) =` constant. The heat capacity of the gas during this process is
View SolutionThe temperature inside a refrigerator is t2 C and the room temperature is t1 C. The amount of heat delivered to the room for each joule of electrical energy consumed ideally will be
View SolutionA refrigerator works between `4^(@)C` and `30^(@)C`. It is required to remove 600 calories of heat every second in order to keep the temperature of the refrigerated space constant. The power requiredd is
(Take, 1 cal = 4.2 Joules)
View SolutionA gas is compressed isothermally to half its initial volume. The same gas is compressed separately through an adiabatic process untill its volume is again reduced to half. Then
View Solution4.0 g of a gas occupies `22.4 L` at NTP. The specific heat capacity of the gas at constant volume is `50 KJ^(-1)`. If the speed of sound in this gas at NTP is `952 ms^(-1)`, then the heat capacity at constant pressure is
(Take gas constant `R = 8.3 JK^(-1) mol^(-1)` )
View Solutionthe coefficient of performance of a refrigerator is 5. If the temperature inside freezer is `-20^(@)C`, the temperature of the surrounding to which it rejects heat is
View SolutionAn ideal gas is compressed of half its initial volume by means of several process. Which of the process results in the maximum work done on the gas ?
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure
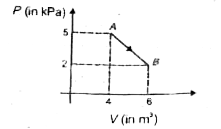
The change to internal energy of the gas during the transition is
View SolutionA Carnot engine, having an efficiency of `eta= 1/10` as heat engine, is used as a refrigerator. If the work done on the system is 10 J, the amount of energy absorbed from the reservoir at lower temperature is
View SolutionFigure below shows two paths that may be taken by a gas to go from a state A to a state C . In process AB , 400 J of heat is added to the system and in process BC , 100 J of heat is added to the system . The heat absorbed by the system in the process AC will be
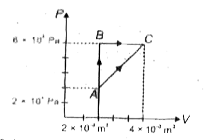
View SolutionA monatomic gas at a pressure P, having a volume V expands isothermally to a volume 2 V and then adiabatically to a volume 16 V. The final pressure of the gas is ( take `gamma=5/3`)
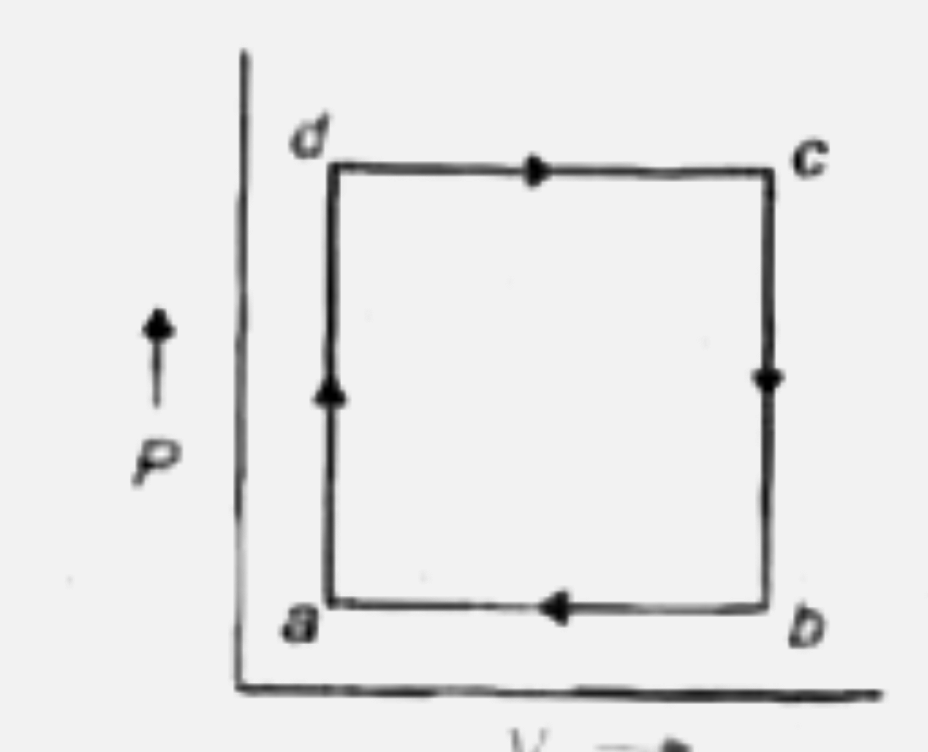
View SolutionA thermodynamic system undergoes cyclic process ABCDA as shown in figure. The work done by the system is
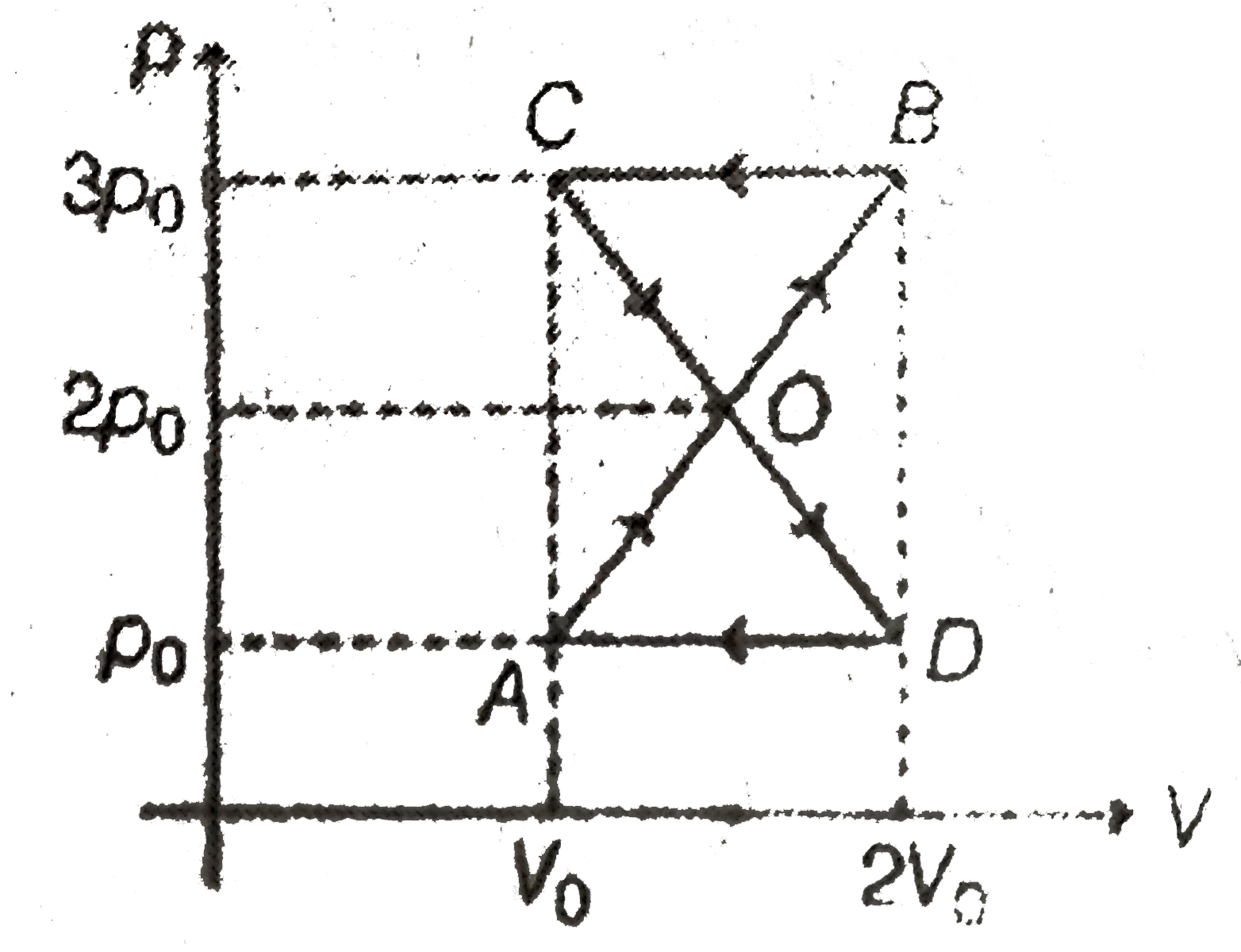
View SolutionA gas is taken through the cycle `A rarr B rarr C rarr A`, as shown. What is the net work done by the gas ?
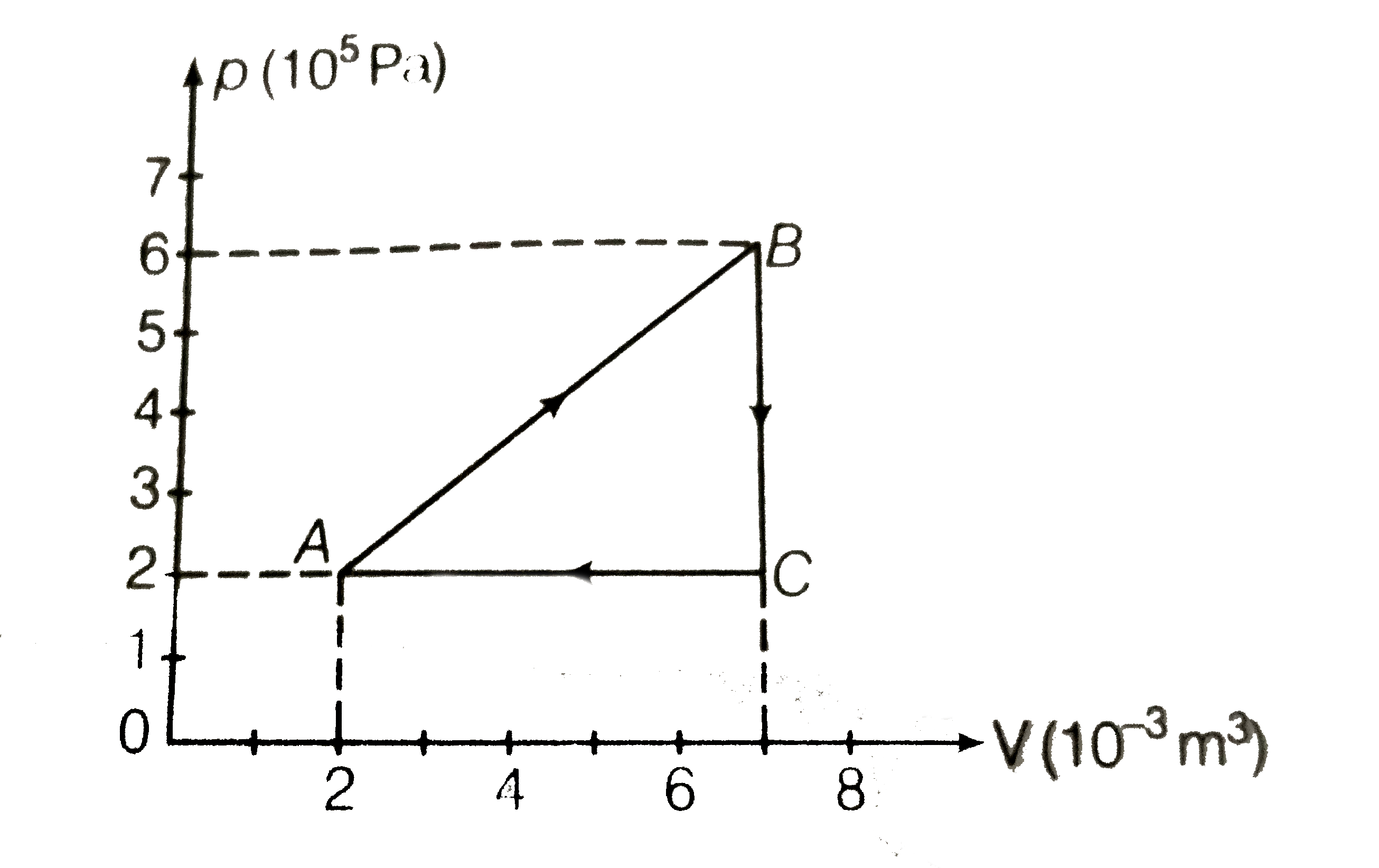
View SolutionThe molar specific heats of an ideal gas at constant pressure and volume are denoted by `C_(p)` and `C_(v)` respectively. If `gamma = (C_(p))/(C_(v))` and R is the universal gas constant, then `C_(v)` is equal to
View SolutionDuring an adiabatic process, the pressure of gas is found to be proportional to the cube of its absolute temperature. The ratio of `(C_(p,m)//C_(v,m))` for gas is :
View SolutionIn the given `(V - T)` diagram, what is the relation between pressures `p_(1)` and `p_(2)` ?

View SolutionOne mole of an ideal gas goes form an initial stateA to final state B via two processes : It first undergoes iosthermal expansion from vluem V to 3V and then its volume is reduced from 3V to V at constatn pressure.The correct P-V diagram rpresenting the two processes is
View SolutionA thermodynamics system is taken trough the cycle ABCD as shown in figure. Heat rejected by the gas during the cycle is:
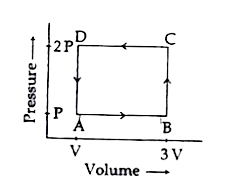
View SolutionAn ideal gas goes from state A to state B via three different processes as indicated in the P-V diagram -

If `Q_(1),Q_(2),Q_(3)` indicate the heat absorbed by the gas along the three process and `DeltaU_(1),DeltaU_(2),DeltaU_(3)`, indicate the change in internal energy along the three processes respectively, then -
View SolutionDuring an isothermal expansion , a confined ideal gas does -150J of work against its surroundings This implies that
View SolutionA mass of diatomic gas (`gamma` = 1.4) at a pressure of 2 atmosphere is compressed adiabatically so that its temperature rises from `27^(@)C " to " 927^(@)C`. The pressure of the gas in the final state is
View SolutionIf `Delta U` and `Delta W` represent the increase in internal energy and work done by the sytem respectively in a thermodynamical process, which of the following is true ?
View SolutionIf `C_(p)` and `C_(v)` denote the specific heats (per unit mass) of an ideal gas of molecular weight M.-
Where R is the molar gas constant
View SolutionA monoatomic gas at pressure `P_(1)` and volume `V_(1)` is compressed adiabatically to `1//8^(th)` its original volume. What is the final pressure of gas -
View SolutionIn thermodynamic processes which of the following statements is not true ?
View SolutionThe internal energy change in a system that has absorbed 2 kcal of heat and done 500 J of work is
View SolutionIf Q, E and W denote respectively the heat added, change in internal energy and the work done in a closed process, then
View SolutionAt `10^(@)C` the value of the density of a fixed mass of an ideal gas divided by its pressure is x. At `110^(@)C` this ratio is
View SolutionThe efficiency of a heat engine is `1//6`Its efficiency double when the temperature of sink decrease by `62^(@)C` its efficiency doubles.Then,What is the temperature of source?
View SolutionA Carnot engine whose sink is at `300K` has an efficiency of `40%`. By how much should the temperature of source be increased so as to increase its efficiency by `50%` of original efficiency.
View SolutionThe molar specific heat at constant pressure of an ideal gas is `(7/2)R`. The ratio of specific heat at constant pressure to that at constant volume is:-
View SolutionWhich of the following processes is reversible
View SolutionAn ideal gas heat engine operates in Carnot cycle between `227^(@)C` and `127^(@)C`. It absorbs `6 xx 10^(4)` cal of heat at highter temperature. Amount of heat converted to work is
View SolutionA system is taken from state a to state c by two paths abc and abc as shown in the figure. The internal energy at a is `U_a = 10J`. Along the path adc the amount of heat absorbed `deltaQ_1 = 50 J` and the work obtained `deltaW_1 = 20J` whereas along the path abc the heat absorbed `deltaQ_2 = 36J`. The amount of work along the path abc is
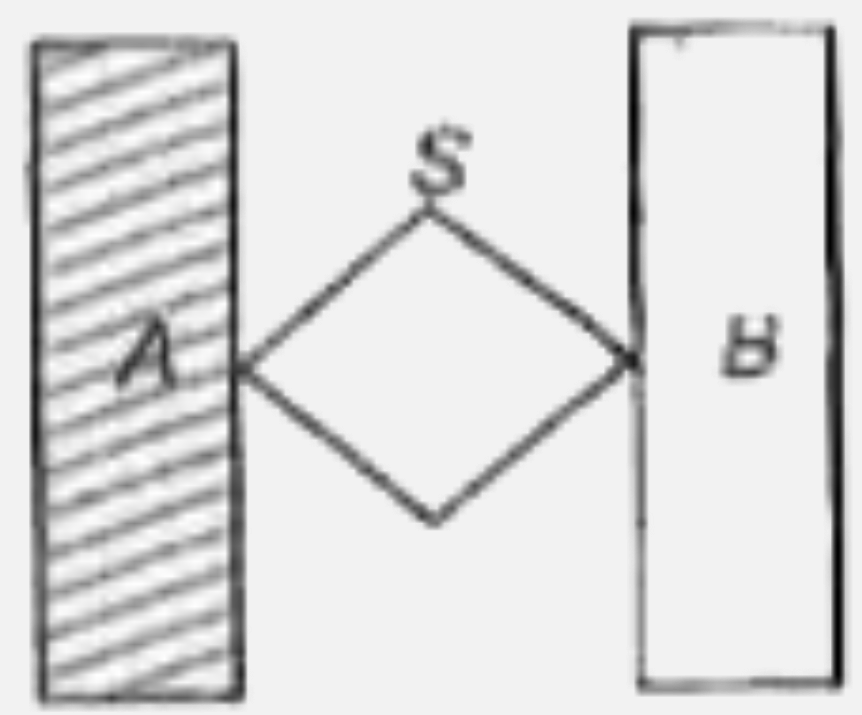
View SolutionConsider two insulated chambers (A,B) of same volume connected by a closed knob ,S. 1 mole of perfect gas is confined in chamber A. What is the change in entropy of gas when knob S is opened ?
View SolutionA Carnot engine has efficiency 25%. It operates between reservoirs of constant temperatuers with temperature difference of `80^@C`. What is the temperature of the low -temperature reservoir ?
View SolutionIn an adiabatic change the pressure and temperature of monoatomic gas are related as `P prop T^(c )` where C equal
View SolutionAn ideal Carnot engine, whose efficiency is `40%` receives heat at 500 K. If its efficiency is `50%`, then the intake temperature for the same exhaust temperature is
View SolutionA diatomic gas initially at `18^(@)C` is compressed adiabatically to one-eight of its original volume. The temperature after compression will be
View SolutionAn ideal gas underging adiabatic change has the following pressure-temperature relationship
View SolutionA sample of gas expands from volume `V_(1)` to `V_(2)`. The amount of work done by the gas is greater when the expansion is
View SolutionThe efficiency of a Carnot engine operating between temperatures of `100^(@)C` and `-23^(@)C` will be
View SolutionWe consider a thermodynamic system. If `Delta U` respresents the increase in its internal energy and W the work done by the system, which of the following statements is true ?
View SolutionIf the ratio of specific heat of a gas at constant pressure to that at constant volume is `gamma`, the change in internal energy of a mass of gas when the volume changes from V to 2V at constant pressure p is
View SolutionAn ideal gas at `27^(@)C` is compressed adiabatically to `(8)/(27)` of its original volume. The rise in temperature is `(gamma = (5)/(3))`
View SolutionTwo ideal Carnot engines operate in casade (all heat given up by one engine is used by the other engine to produce work) between temperatures, `T_(1)` and `T_(2)`. The temperature of the hot reservoir of the first engine is `T_(1)` and the temperature of cold reservoir of the second engine is `T_(2)`. T is temperature of the sink of first engine which is also the source for the second engine. How is T related to `T_(1)` and `T_(2)`, if both the engines perform equal amount of work?
View SolutionThe (W/Q) for a Carnot engine is 1/6. Now the temperature of sink is reduced by `62^@C`, then this ratio becomes twice, therefore the initial temperatureof the sink and source are respectively
View SolutionThe temperature of source and sink of a heat engine are `127^(@)C` and `27^(@)C` respectively. As inventor claims its efficiency to be `26%`, then,
View SolutionThe efficiency of carnot engine is 50% and temperature of sink is 500K. If temperature of source is kept constant and its efficiency raised to 60%, then the required temperature of the sink will be : -
View SolutionAn ideal gas heat engine operates in a Carnot cycle between `27^(@)C` and `127^(@)C`. It absorbs `6 kcal` at the higher temperature. The amount of heat (in kcal) converted into work is equal to
View SolutionOne mole of an ideal gas at an initial temperature of T K does 6 R joules of work adiabatically. If the ratio of specific heats of this gas at constant pressure and at constant volume is `5/3` , the final temperature of gas will be :-
View SolutionThe amount of heat energy required to raise the temperature of 1 g of helium at NTP, from `T_(1)K` to `T_(2)K` is
View SolutionWhich of the following relations does not give the equation of an adiabatic process, where tems have their usual meaning ?
View SolutionAccording to C.E van der Waal, the interatomic potential varies with the average interatomic distance (R) as
View SolutionA gas at pressure `p_(0)` is contained in a vessel. If the masses of all the molecules are halved and their speeds doubled, the resulting pressure would be
View SolutionThe mean free path of collision of gas melecules varies with its diameter (d) of the molecules as
View SolutionAt `0 K`, which of the following properties of a gas will be zero ?
View SolutionThe units of constant b used in van der Waals' equation are ………….. .
View SolutionThe degrees of freedom of a triatomic gas is
View SolutionTo find out degree of freedom, the correct expression is:
View SolutionThe equation of state for 5 g of oxygen at a pressure P and temperature T, when occupying a volume V, will be
View Solution
ASSIGNMENT (SECTION -C) (Previous Year Questions) questions and complete solutions for chapter THERMODYNAMICS of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS THERMODYNAMICS
- ASSIGNMENT (SECTION -A) (Objective Type Questions)
- ASSIGNMENT (SECTION -B) (Objective Type Questions)
- ASSIGNMENT (SECTION -C) (Previous Year Questions)
- ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
- Assignment (Section-A) Objective Type Questions (one option is correct)
- Assignment (Section-B) Objective Type Questions (one option is correct)
- Assignment (Section-C) Objective Type Questions (More than one option are correct)
- Assignment (Section-D) Linked comprehension Type questions
- Assignment (Section-E) Assertion-Reason Type Questions
- Assignment (Section-F) Matrix-Match type Question
- Assignment (Section-G) Integer Answer Type Questions
- Assignment (Section-H) Multiple True-False Type Question
- Assignment (Section-I) Subjective Type
- Assignment (Section-J) Aakash Challengers Questions
- Example
- EXERCISE
- TRY YOURSELF
- Try Youself