Complete Solutions to EXAMPLE of chapter DUAL NATURE OF RADIATION AND MATTER of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | DUAL NATURE OF RADIATION AND MATTER |
| AAKASH INSTITUTE | EXAMPLE |
| Number Of Questions | 57 |
| Academic Year | 2023-24 |
Calculate the energy associated with one photon of the radian of wavelength 4000Å.
View SolutionWork function of sodium is 2.3 eV. Does sodium show photoelectric emission for orange light `(lambda=6800Å)`?
Given `h=6.63xx10^(-34)Js`
View SolutionThe threshold frequency of a material is `2xx10^14` Hz. What is its work function in eV ?
View SolutionFind the maximum velocity of photoelectrons emitted by radiation of frequency `3 xx 10^(15)` Hz from a photoelectric surface having a work function of 4.0 eV. Given `h=6.6 xx 10^(-34)` Js and 1 eV = `1.6 xx 10^(-19)` J.
View SolutionLight of wavelength 2000 Å falls on a metallic surface whose work function is 4.21 eV. Calculate the stopping potential
View SolutionIf the speed of photoelectrons is ` 10^(4) m//s ` , what shold be the frequency of the incident radiation on a potassium metal? Given : Work function of potasslum = 2.3 eV .
View SolutionThe maximum velocity of an electron emitted by light of wavelength `lambda` incident on the surface of a metal of work function `phi`, is
Where h = Planck's constant , m = mass of electron and c = speed of light.
View SolutionLight of wavelength `2475 Å` is incident on barium. Photoelectrons emitted describe a circle of radius `100 cm` by a magnetic field of flux density `(1)/(sqrt(17)) xx 10^(-5) Tesla`.
Work function of the barium is (Given `(e )/(m) = 1.7 xx 10^(11)`)
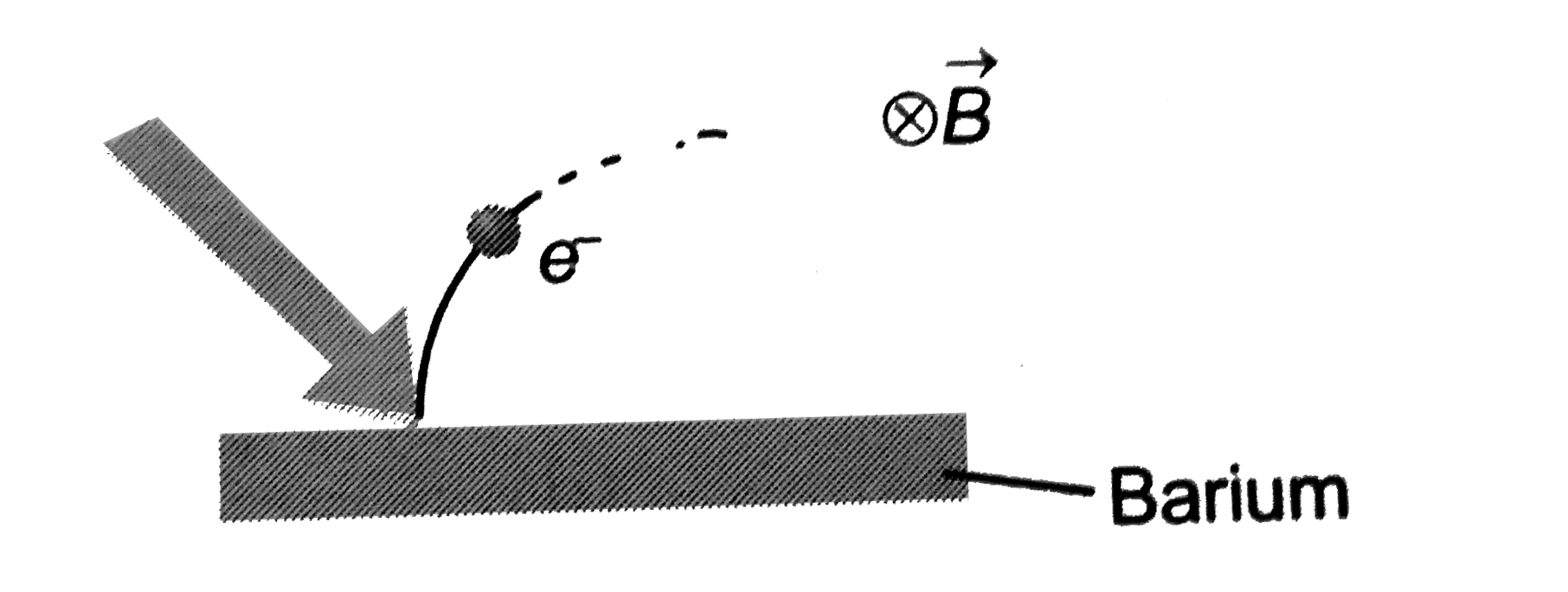
View SolutionMonochromatic light if wavelegath 3000 A is incident on a surface area ` 4 cm^(2)` . If intensity of light is ` 150 mW//m^(2)` , find the rate at which photons strike the target .
View SolutionIf light of frequency `8.2xx10^14` Hz is incident on the metal , cut-off voltage for photoelectric emission is 2.03 V.Find the threshold frequency . Given h=`6.63xx10^(-34) ` Js , e=`1.6xx10^(-19)` C.
View SolutionLight of wavelength 4000Å is incident on barium. Photoelectrons emitted describe a circle of radius 50 cm by a magnetic field of flux density `5.26xx10^-6 tesla`. What is the work function of barium in eV? Given `h=6.6xx10^(-34)Js , e=1.6xx10^(-19)C, m_e=9.1xx10^(-31)kg.`
View SolutionThe wavelength of a photon is 1.4 Å. It collides with an electron. The energy of the scattered electron is `4.26xx10^(-16)` J. Find the wavelength of photon after collision.
View SolutionThe wavelength `lambda` of a photon and the de-Broglie wavelength of an electron have the same value. Show that the energy of the photon is `(2 lambda mc)/h` times the kinetic energy of the electron, Where m,c and h have their usual meanings.
View SolutionIf de Broglie wavelength of an electron is 0.5467 Å,
find the kinetic energy of electron in eV. Given `h=6.6xx10^(-34)` Js ,
e=`1.6xx10^(-19)` C, `m_e=9.11xx10^(-31)` kg.
View SolutionThe ratio of momenta of an electron and an `alpha`-particle which are accelerated from rest by a potential difference of 100 V is
View SolutionFind the ratio of velocities of proton and `alpha`-particle if the de Broglie wavelengths of both the particles is same.
View SolutionThe de- broglie wavelength of an electron in the first bohr orbit is
View SolutionFind out the energy that should be added to an electron is terms of initial energy to reduce its de Broglie wavelengths from ` 10^(-10) " m to " 0.5 xx 10^(-10)` m .
View SolutionThe de - Broglie wavelength of a particle moving with a velocity `2.25 xx 10^(8) m//s` is equal to the wavelength of photon. The ratio of kinetic energy of the particle to the energy of the photon is (velocity of light is `3 xx 10^(8) m//s`
View SolutionWhen the momentum of a proton is changed by an amount ` p_(0)` the corresponding change in the de Brolie wavelength is found to be 0.25% . Find the original momentum of the photon .
View SolutionA proton and an `alpha`-particle are accelerated through the same potential difference. The ratio of Broglie wavelength `lamda_(p)` to that of `lamda_(alpha)` is
View SolutionThe ratio of de - Broglie wavelength of `alpha `- particle to that of a proton being subjected to the same magnetic field so that the radii of their path are equal to each other assuming the field induction vector `vec(B)` is perpendicular to the velocity vectors of the `alpha` - particle and the proton is
View SolutionThe eye can detect `5xx10^(4)` photons `(m^2s)^(-1)` of green light (`lamda=5000A)`, whole ear can detect `10^(-13)Wm^(2)` . As a power detector, which is more sensitive and by what factor?
View SolutionThe photoelectric work function for sodium is 2.7 eV. If light of frequency `9.0xx10^14` Hz falls on sodium, find (a) the stopping potential, (b)the kinetic energy of the most energetic electrons ejected , and (c ) the speed of those electrons.
View SolutionThe stopping potential for photoelectrons ejected from a surface by 375 nm photons is 1.870 V. Calculate the stopping potential for 600 nm photons .
View SolutionFind the threshold wavelength of light that would produce photoelectrons for a silver surface . The work function for silver is 4.8 eV
View SolutionCalculate the energy of a photon of blue light, `lambda`=450 nm in air (or vacuum).
View SolutionEstimate how many visible light photons a 100 W light bulb emits per second . Assume the bulb has a typical efficiency of about 3% (that is 97% of the energy goes to heat)
View SolutionSuppose the `10^19` photons emitted per second from the 100 W lightbulb in were all focused onto a piece of black paper and absorbed. (a)Calculate the momentum of one photon and (b)estimate the force all these photons could exert on the paper.
View SolutionCalculate the de-Broglie wavelength of a 0.20 kg ball moving with a speed of 15 m/s
View SolutionThe wavelength associated with an electron, accelerated through a potential difference of `100V`, is of the order of
View SolutionAn electron and a photon have the same de Broglie wavelength. Which one of these has higher kinetic energy?
View SolutionFind the ratio of de Broglie wavelength of molecules of hydrogen and helium which are at temperatures ` 27^(@) " and " 127^(@) C ` respectively
View SolutionA proton and an `alpha`-particle are accelerated through the same potential difference. The ratio of Broglie wavelength `lamda_(p)` to that of `lamda_(alpha)` is
View SolutionCalculate the energy associated with one photon of the radian of wavelength 4000Å.
View SolutionWork function of sodium is 2.3 eV. Does sodium show photo-electric emission for light of wavelength 6800 Å ?
View SolutionThe threshold frequency of a material is `2xx10^14` Hz. What is its work function in eV ?
View SolutionFind the maximum velocity of photoelectrons emitted by radiation of frequency `3xx10^15` Hz from a photoelectric surface having a work function 4.0 eV
View SolutionLight of wavelength 2000 Å falls on a metallic surface whose work function is 4.21 eV. Calculate the stopping potential
View Solutionif the speed of photoelectrons is `10^4` m/s, what should be the frequency of the incident radiation on a potassium metal ? Given : Work function of potassium =2.3 eV
View SolutionFind the maximum velocity of an electron emitted by light of wavelength `lambda` incident on the surface of a metal of work function `phi`.
View SolutionLight of wavelength 2475 Å is incident on barium . Photo electrons emitted describe a circle of radius 100 cm by a magnetic field of flux density `1/sqrt17xx10^(-5)` tesla. Find the work function of the barium . (Given `e/m=1.7xx10^11`)
View SolutionMonochromatic light of wavelength `3000 Å` is incident on a surface area `4 cm^(2)`. If intensity of light is `150 m W//m^(2)` , then rate at which photons strike the target is
View SolutionIf light of frequency `8.2xx10^14` Hz is incident on the metal , cut-off voltage for photoelectric emission is 2.03 V.Find the threshold frequency . Given h=`6.63xx10^(-34) ` Js , e=`1.6xx10^(-19)` C.
View SolutionWhen light of wavelangth `4000 Å` is incident on a barium emitter , emitted photo electrons in a transverse magnetic field strength ` B = 5.2 xx 10^(-6)` T moves in a circular path . Find the radius of the circle . Given work function of barium is 2.5 eV and mass of electron is ` 9.1 xx 10^(-31)` kg .
` e = 1.6 xx 10^(-19) C , h = 6.6 xx 10^(34) Js ` .
View SolutionThe wavelength of a photon is 1.4 Å. It collides with an electron. The energy of the scattered electron is `4.26xx10^(-16)` J. Find the wavelength of photon after collision.
View SolutionIf the energy of the photon is ` (2 lambda_(p)mc)/(h) ` times the kinetic energy of the electron then show then the wavelength ` lambda ` of photon and the de Broglie wavelength of an electron have the same value
(Where m, c and h have their usual meanings .)
View SolutionIf de Broglie wavelength of an electron is 0.5467 Å,
find the kinetic energy of electron in eV. Given `h=6.6xx10^(-34)` Js ,
e=`1.6xx10^(-19)` C, `m_e=9.11xx10^(-31)` kg.
View SolutionThe ratio of momenta of an electron and an `alpha`-particle which are accelerated from rest by a potential difference of 100 V is
View SolutionFind the ratio of velocities of proton and `alpha`-particle if the de Broglie wavelengths of both the particles is same.
View SolutionFind the de Broglie wavelength of revolving electron for the Bohr's first orbit of circumference `2pir`.
View SolutionThe energy that should be added to an electron, to reduce its de-Broglie wavelengths from `10^(-10) m` to `0.5 xx 10^(-10)` m wil be
View SolutionFind the ratio of kinetic energy of the particle to the energy of the photon . If the de Broglie wavelength of a particle moving with a velocity ` 2.25xx 10^(8) m//s ` is equal to the wavelength of photon .
View SolutionWhen the mkomentum of a proton is changed by an amount `p_(0)`, the corresponding change in the de-Broglie wavelength is found to be `0.25%`. Then, the original momentum of the proton was
View SolutionA proton and an alpha - particle are accelerated through same potential difference. Then, the ratio of de-Broglie wavelength of proton and alpha-particle is
View SolutionFind the ratio of de Broglie wavelength of an `alpha`-particle to that of a photon being subjected to the same magnetic field so that the radii of their path are equal to each other assuming the field induction vector `vecB` is perpendicular to the velocity vectors of the `alpha`-particle and proton.
View SolutionThe eye can detect `5xx10^(4)` photons `(m^2s)^(-1)` of green light (`lamda=5000A)`, whole ear can detect `10^(-13)Wm^(2)` . As a power detector, which is more sensitive and by what factor?
View Solution
EXAMPLE questions and complete solutions for chapter DUAL NATURE OF RADIATION AND MATTER of AAKASH INSTITUTE ENGLISH of Class 12
All Exercises from AAKASH INSTITUTE Class 12 PHYSICS DUAL NATURE OF RADIATION AND MATTER
- ASSIGNMENT (SECTION-A)
- ASSIGNMENT (SECTION-B)
- ASSIGNMENT (SECTION-C)
- ASSIGNMENT (SECTION-D)
- ASSIGNMENT SECTION C. Objective (More than one answer)
- ASSIGNMENT SECTION A. Objective (Only one answer)
- ASSIGNMENT SECTION B.Objective (Only one answer)
- ASSIGNMENT SECTION D.Linked Comprehension
- ASSIGNMENT SECTION E.Assertion-Reason
- ASSIGNMENT SECTION F.Matrix Match
- ASSIGNMENT SECTION G. Integer
- ASSIGNMENT SECTION H.Multiple True-False
- ASSIGNMENT SECTION I.Subjective
- ASSIGNMENT SECTION J.Aakash Challengers
- EXAMPLE
- EXERCISE
- Try Yourself