Complete Solutions to Exercise (More Than One Correct Option Type Questions) of chapter THEORY OF EQUATIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | THEORY OF EQUATIONS |
| ARIHANT MATHS | Exercise (More Than One Correct Option Type Questions) |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
If `0 lt a lt b lt c` and the roots `alpha,beta` of the equation `ax^2 + bx + c = 0` are non-real complex numbers, then
View SolutionIf A, G and H are the arithmetic mean, geometric mean and harmonic mean between unequal positive integers. Then, the equation `Ax^2 -|G|x- H=0` has
(a) both roots are fractions (b) atleast one root which is negative fraction (c) exactly one positive root (d) atleast one root which is an integer
View SolutionThe adjoining graph of `y=ax^(2)+bx+c` shows that
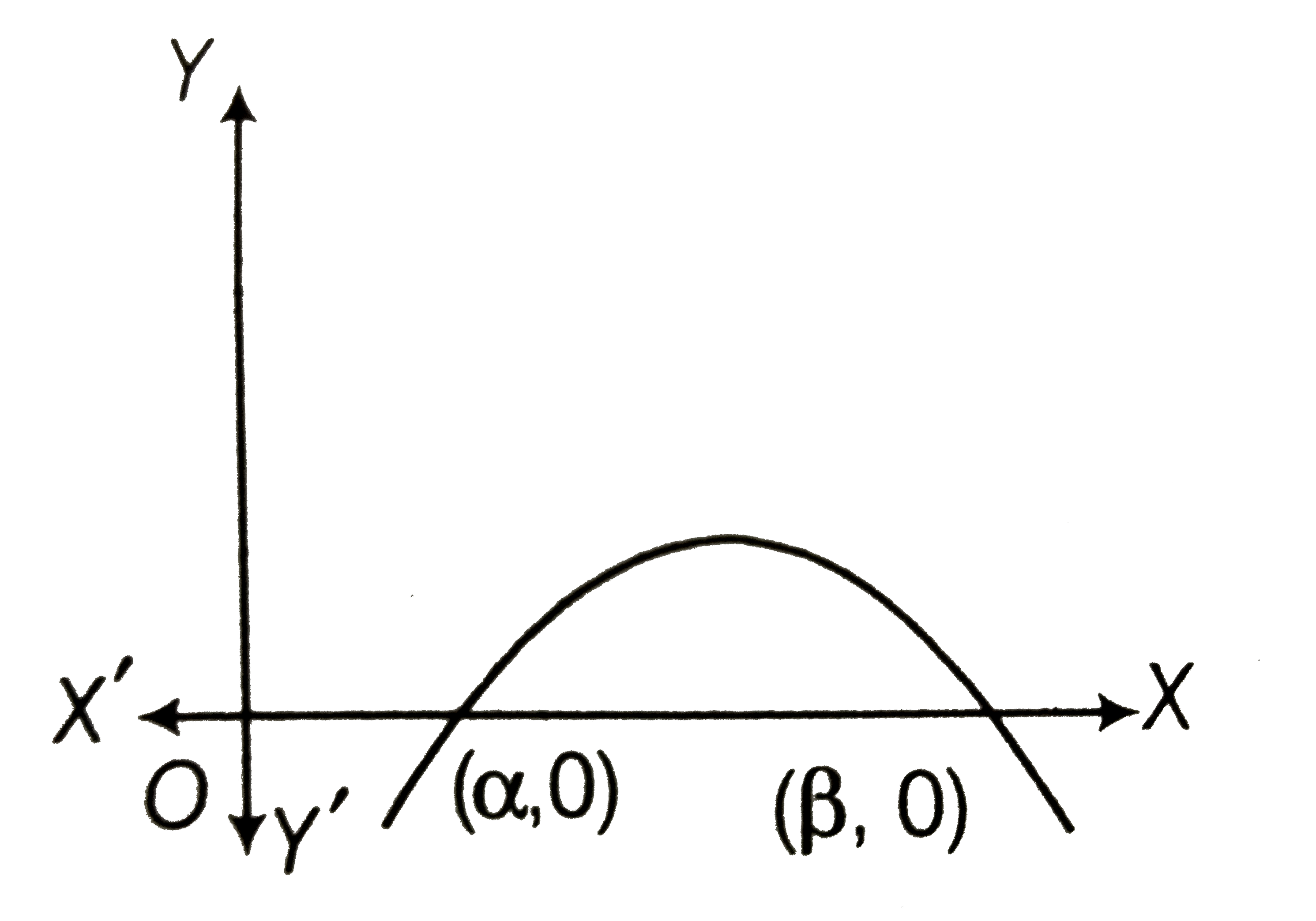
View Solution`ax^2 + bx + c = 0(a > 0),` has two roots `alpha and beta` such `alpha < -2 and beta > 2,` then
View SolutionIf `b^(2)ge4ac` for the equation `ax^(4)+bx^(2)+c=0` then all the roots of the equation will be real if
View SolutionIf the roots of the equation `x^(3) + bx^(2) + cx - 1 = 0` form an increasing G.P., then b belongs to which interval ?
View SolutionLet `f(x) = a x^2 + bx + c`, where `a, b, c in R, a!=0`. Suppose `|f(x)| leq1, x in [0,1]`, then
View Solution`cosα` is a root of the equation `25x^2+5x−12=0,−1 lt x lt 0`, then find the value of `sin2α` is:
View SolutionIf `a,b, c epsilon R(a!=0)` and `a+2b+4c=0` then equatio `ax^(2)+bx+c=0` has
View SolutionFor which of the following graphs the quadratic expression `y=ax^(2)+bx+c` the product `abc` is negative ?
View SolutionIf `a, b in R` and `ax^2 + bx +6 = 0,a!= 0` does not have two distinct real roots, then :
View SolutionIf `x^3+3x^2-9x+c` is of the form `(x-alpha)^2(x-beta)` then `c` is equal to
View SolutionIf `a x^2+(b-c)x+a-b-c=0` has unequal real roots for all `c in R ,t h e n` `b<0 a >0`
View SolutionIf the equation whose roots are the squares of the roots of the cubic `x^3-a x^2+b x-1=0` is identical with the given cubic equation, then (A) `a=0,b=3` (B) `a=b=0` (C) `a=b=3` (D) `a ,b ,` are roots of`x^2+x+2=0`
View Solution`ax^2 + bx + c = 0(a > 0),` has two roots `alpha and beta` such `alpha < -2 and beta > 2,` then
View Solution
Exercise (More Than One Correct Option Type Questions) questions and complete solutions for chapter THEORY OF EQUATIONS of ARIHANT MATHS (ENGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS THEORY OF EQUATIONS
- Examples
- Exercise (Matching Type Questions)
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Single Integer Answer Type Questions)
- Exercise (Single Option Correct Type Questions)
- Exercise (Statement I And Ii Type Questions)
- Exercise (Subjective Type Questions)
- Exercise For Session 1
- Exercise For Session 2
- Exercise For Session 3
- Exercise For Session 4
- Exercise For Session 5
- MATCH TYPE
- SCQ_TYPE