Complete Solutions to Exercise (Passage Based Questions) of chapter THEORY OF EQUATIONS of Class 12 book with complete answers and questions

If G and L are the greatest and least values of the expression`(2x^(2)-3x+2)/(2x^(2)+3x+2), x epsilonR` respectively.
The least value of `G^(100)+L^(100)` is
(a) `2^(100)` (b) `3^(100)` (c) `7^(100)` (d) none of these

If G and L are the greatest and least values of the expression`(2x^(2)-3x+2)/(2x^(2)+3x+2), x epsilonR` respectively.
G and L are the roots of the equation

If G and L are the greatest and least values of the expression`(2x^(2)-3x+2)/(2x^(2)+3x+2), x epsilonR` respectively. If `L^(2)ltlamdaltG^(2), lamda epsilon N` the sum of all values of `lamda` is

If the roots of the equaion `x^4-12 x^3+c x^2+dx+81=0` are positive then the value of c is The value of d is. Roots of the equation 2cx+d=0 is

If the roots of the equaion `x^4-12 x^3+c x^2+dx+81=0` are positive then the value of c is The value of d is. Roots of the equation 2cx+d=0 is

If the roots of the equaion `x^4-12 x^3+c x^2+dx+81=0` are positive then the value of c is The value of d is. Roots of the equation 2cx+d=0 is

In the given figue vertices of `DeltaABC` lie on `y=f(x)=ax^(2)+bx+c`. The `DeltaABC` is right angled isosceles triangle whose hypotenuse `AC=4sqrt(2)` units.

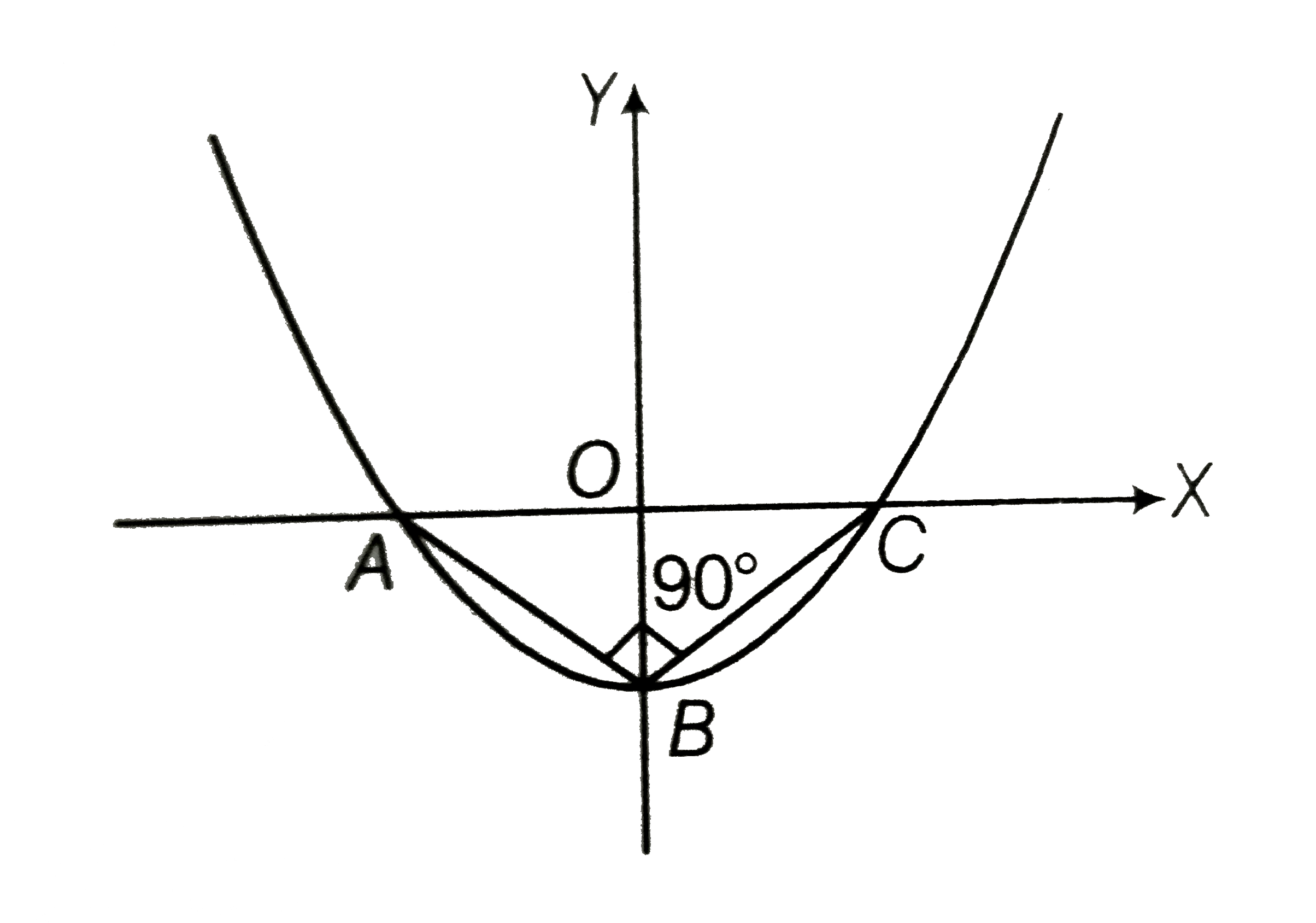
`y=f(x)` is given by

In the given figue vertices of `DeltaABC` lie on `y=f(x)=ax^(2)+bx+c`. The `DeltaABC` is right angled isosceles triangle whose hypotenuse `AC=4sqrt(2)` units.

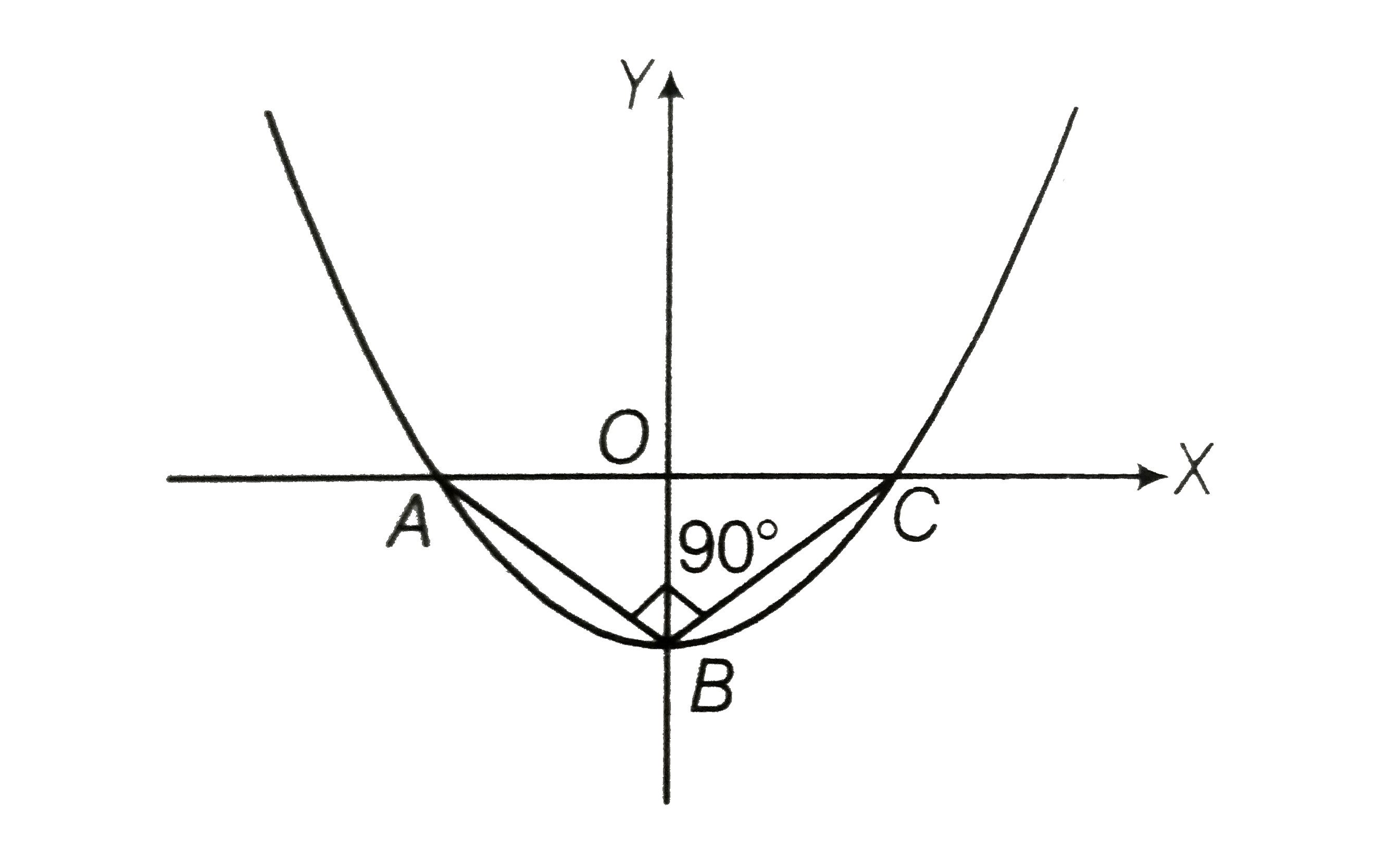
Minimum valueof `y=f(x)` is

In the given figue vertices of `DeltaABC` lie on `y=f(x)=ax^(2)+bx+c`. The `DeltaAB` is right angled isosceles triangle whose hypotenuse `AC=4sqrt(2)` units.

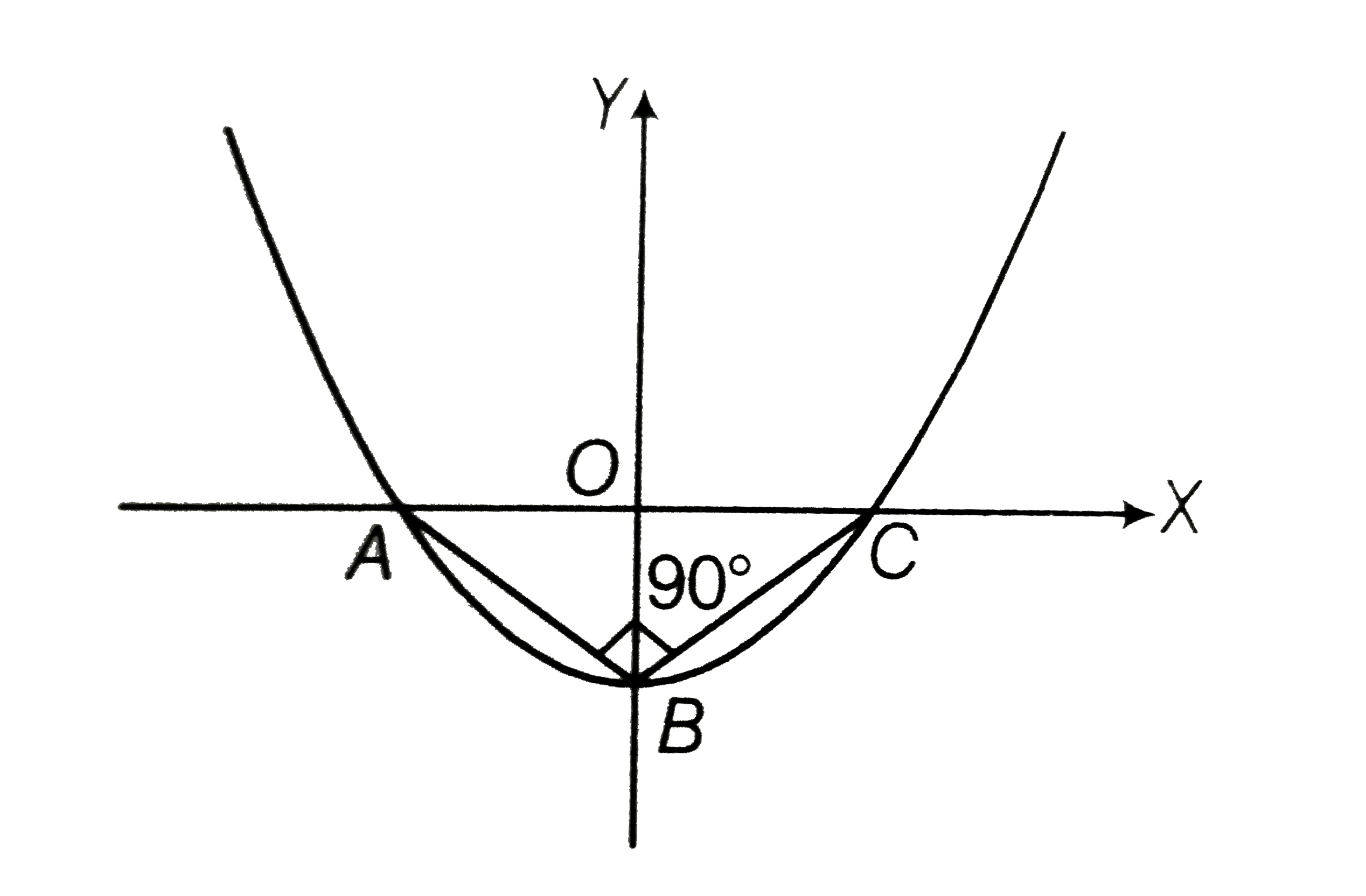
Number of integral value of `lamda` for which `(lamda)/2` lies between the roots of `f(x)=0`, is

Let `f(x) = x2 + b_1x + c_1. g(x) = x^2 + b_2x + c_2`. Real roots of `f(x) = 0` be `alpha, beta` and real roots of `g(x) = 0` be `alpha+gamma, beta+gamma`. Least values of `f(x)` be `- 1/4`Least value of `g(x)` occurs at `x=7/2`

Let `f(x) = x2 + b_1x + c_1. g(x) = x^2 + b_2x + c_2`. Real roots of `f(x) = 0` be `alpha, beta` and real roots of `g(x) = 0` be `alpha+gamma, beta+gamma`. Least values of `f(x)` be `- 1/4`Least value of `g(x)` occurs at `x=7/2`

Let `f(x)=x^(2)+bx+c` and `g(x)=x^(2)+b_(1)x+c_(1)` Let the real roots of `f(x)=0` be `alpha, beta` and real roots of `g(x)=0` be `alpha +k, beta+k` fro same constant `k`. The least value fo `f(x)` is `-1/4` and least value of `g(x)` occurs at `x=7/2` The roots of `g(x)=0` are

If `ax^2-bx + c=0` have two distinct roots lying in the interval `(0,1); a, b,in N`, then the least value of a , is

If `ax^(2)+bx+c=0` have two distinct roots lying int eh interval `(0,1),a,b,c ` ` epsilon N` The least value of `b` is

If `ax^(2)-bx+c=0` have two distinct roots lying in the interval `(0,1),a,b,c Epsilon N` The least value of `log_(5)abc` is

If `2x^(3)+ax^(2)+bx+4=0` (a and b are positive real numbers) has three real roots.
The minimum value of `a^(3)` is a. 108 b. 216 c. 432 d. 864

If `2x^(3)+ax^(2)+bx+4=0` (a and b are positive real numbers) has three real roots.
The minimum value of `b^(3)` is a. 108 b. 216 c. 432 d. 864

If `2x^(3)+ax^(2)+bx+4=0` (a and b are positive real numbers) has three real roots.
The minimum value of `(a+b)^(3)` is

If `alpha, beta, gamma` are the roots of the equation `x^(4)+Ax^(3)+Bx^(2)+Cx+D=0` such that `alpha beta= gamma delta=k` and A,B,C,D are the roots of `x^(4)-2x^(3)+4x^(2)+6x-21=0` such that `A+B=0`
The value of `C/A` is

If `alpha, beta, gamma, delta` are the roots of the equation `x^(4)+Ax^(3)+Bx^(2)+Cx+D=0` such that `alpha beta= gamma delta=k` and A,B,C,D are the roots of `x^(4)-2x^(3)+4x^(2)+6x-21=0` such that `A+B=0` The value of `(alpha+beta)(gamma+delta)` is terms of B and `k` is

If `alpha, beta, gamma` are the roots of the equation `x^(4)+Ax^(3)+Bx^(2)+Cx+D=0` such that `alpha beta= gamma delta=k` and A,B,C,D are the roots of `x^(4)-2x^(3)+4x^(2)+6x-21=0` such that `A+B=0`
The correct statement is