Complete Solutions to Examples of chapter AREA OF BOUNDED REGIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | AREA OF BOUNDED REGIONS |
| ARIHANT MATHS | Examples |
| Number Of Questions | 74 |
| Academic Year | 2023-24 |
Mark the region represtented by `3x+4yle12`.
View SolutionSketch the curve `y=x^3`.
View SolutionSketch the curve `y=x^3-4x`.
View SolutionSketch the curve `y=(x-1)(x-2)(x-3)`.
View SolutionSketch the graph for `y=x^(2)-x`.
View SolutionSketch the curve `y="sin"2x`.
View SolutionSketch the curve `y="sin"^(2)x`.
View SolutionConstruct the graph for `f(x)=(x^(2)-1)/(x^(2)+1)`.
View SolutionConstruct the graph for `f(x)=x+(1)/(x)`.
View SolutionConstruct the graph for `f(x)=(1)/(1+e^(1//x))`.
View SolutionSketch the graph `y=|x+1|dot` Evaluate `int_(-4)^2\ |x+1|dxdot` What does the value of this integral represent on the graph?
View SolutionThe area inside the parabola `5x^2-y=0` but outside the parabola `2x^2-y+9=0` is (a) `12sqrt(3)` sq units (b) `6sqrt(3)` sq units (c) `8sqrt(3)` sq units (d) `4sqrt(3)` sq units
View SolutionThe area enclosed by `y = x(x - 1)(x - 2)` and x-axis, is given by
View SolutionThe area between the curve `y=2x^4-x^2,` the axis, and the ordinates of the two minima of the curve is 11/60 sq. units (b) 7/120 sq. units 1/30 sq. units (d) 7/90 sq. units
View SolutionSketch the curves and identify the region bounded by the curves `x=1/2,x=2,y=logxa ny=2^xdot` Find the area of this region.
View SolutionFind the area of region : `{(x,y) : 0 le y le x^(2) + 1, 0 le y le x + 1,0 le x le 2}`.
View SolutionThe area common to the region determined by `y >= sqrtx` and `x^2 + y^2 < 2` has the value
View SolutionFind the area of the figure enclosed by the curve `5x^2+6x y+2y^2+7x+6y+6=0.`
View SolutionIf `f(x)={(sqrt({x}), x !in Z),(1, x in Z):}` and `g(x)={x}^2` then area bounded by f(x) and g(x) for `x in [0,10]` is
View SolutionFind the area of the region bounded by the curves `y=x^(2), y=|2-x^(2)|, and y=2,` which lies to the right of the line x=1.
View SolutionThe area enclosed by the curve `|y|=sin2x,` where `x in [0,2pi].` is
View SolutionLet `f(x)=x^(2), g(x)="cos" x` and `alpha,beta (alpha lt beta)` be the roots of the equation `18x^(2)-19pi x+pi^(2)=0`. Then the area bounded by the curves `u="fog"(x)`, the ordinates `x=alpha, x=beta` and the X-asis is
View SolutionFind the area bounded by the curves `x^2+y^2=25 ,4y=|4-x^2|,` and `x=0` above the x-axis.
View SolutionFind area enclosed by `|x|+|y|=1`.
View SolutionLet `f(x)="max"{sin x,cos x,1/2}`, then determine the area of region bounded by the curves `y=f(x)`, X-axis, Y-axis and `x=2pi`.
View SolutionIf A denotes the area bounded by `f(x)=|("sin"x + "cos"x)/(x)|`, X-axis, `x=pi` and `x=3 pi`,then
View SolutionIf `y=f(x)` makes positive intercepts of 2 and 1 unit on x and y-coordinates axes and encloses an area of `3/4` sq unit with the axes, then `int_0^2 x f'(x)\ dx`, is
View SolutionThe area of the region included between the regions satisfying `min(|x|,|y|) geq1` and `x^2+y^2leq5` is
View SolutionThe area of the region bounded by the curves `y=sqrt[[1+sinx]/cosx]` and `y=sqrt[[1-sinx]/cosx]` bounded by the lines x=0 and `x=pi/4` is
View SolutionLet T be the triangle with vertices `(0,0), (0,c^2 )and (c, c^2)` and let R be the region between `y=cx and y = x^2` where `c > 0` then
View SolutionSuppose fis defined from `R -> [-1,1]` as `f(x)=(x^2-1)/(x^2+1)` where R is the set of real number .then the statement which does not hold is
View SolutionConsider `f(x)={{:(cosx,0lexlt(pi)/(2)),(((pi)/(2)-x)^(2),(pi)/(2)lexltpi):}` such that f is periodic with period `pi`. Then which of the following is not true?
View SolutionConsider the functions f(x) and g(x), both defined from `R rarrR` and are defined as `f(x)=2x-x^(2) and g(x)=x^(n)` where `n in N`. If the area between f(x) and g(x) is 1/2, then the value of n is
View SolutionThe area of the region bounded by the curve `y=e^x` and lines `x=0a n dy=e` is `e-1` (b) `int_1^e1n(e+1-y)dy` `e-int_0^1e^x dx` (d) `int_1^e1nydy`
View SolutionConsider the function `f(x)=x^(3)-8x^(2)+20x-13`
The function `f(x)` defined for `R to R`
View SolutionConsider the function `f(x)=x^(3)-8x^(2)+20x-13`
Area enclosed by `y=f(x)` and the coordinate axes is
View SolutionLet `h(x)-f(x)-g(x)` where `f(x)=sin^4 pi x and g(x)=Inx`. Let `x_0,x_1,x_2,......,x_(n-1)` be the roots of `f(x) = g(x)` in increasing oder.Then the absolute area enclosed by `y = f(x) and y = g(x)` is given by
View SolutionLet `h(x)=f(x)=f_(x)-g_(x)`, where `f_(x)=sin^(4)pix` and `g(x)=In x`. Let `x_(0),x_(1),x_(2) , ....,x_(n+1_` be the roots of `f_(x)=g_(x)` in increasing order.
In the above question, the value of n is
View SolutionLet `h(x)=f(x)=f_(x)-g_(x)`, where `f_(x)=sin^(4)pix` and `g(x)=In x`. Let `x_(0),x_(1),x_(2) , ....,x_(n+1_` be the roots of `f_(x)=g_(x)` in increasing order.
The absolute area enclosed by `y=f_(x)` and `y=g(x)` is given by
View SolutionConsider the function defined implicitly by the equation `y^3-3y+x=0` on various intervals in the real line. If `x in (-oo,-2) uu (2,oo)`, the equation implicitly defines a unique real-valued defferentiable function `y=f(x)`. If `x in (-2,2)`, the equation implicitly defines a unique real-valud diferentiable function `y-g(x)` satisfying `g_(0)=0`.
If `f(-10sqrt2)=2sqrt(2)`, then `f"(-10sqrt(2))` is equal to
View SolutionConsider the function defined implicitly by the equation `y^3-3y+x=0` on various intervals in the real line. If `x in (-oo,-2) uu (2,oo)`, the equation implicitly defines a unique real-valued defferentiable function `y=f(x)`. If `x in (-2,2)`, the equation implicitly defines a unique real-valud diferentiable function `y-g(x)` satisfying `g_(0)=0`.
The area of the region bounded by the curve `y=f(x)`, the X-axis and the line `x=a` and `x=b`, where `-oo lt a lt b lt -2` is
View SolutionConsider the function defined implicitly by the equation `y^3-3y+x=0` on various intervals in the real line. If `x in (-oo,-2) uu (2,oo)`, the equation implicitly defines a unique real-valued defferentiable function `y=f(x)`. If `x in (-2,2)`, the equation implicitly defines a unique real-valud diferentiable function `y-g(x)` satisfying `g_(0)=0`.
If `f(-10sqrt2)=2sqrt(2)`, then `f"(-10sqrt(2))` is equal to
View SolutionA curve `y=f(x)` passes through point `P(1,1)` . The normal to the curve at `P` is a `(y-1)+(x-1)=0` . If the slope of the tangent at any point on the curve is proportional to the ordinate of the point, then the equation of the curve is (a) `( b ) (c) y=( d ) e^(( e ) (f) K(( g ) (h) x-1( i ))( j ))( k ) (l)` (m) (b) `( n ) (o) y=( p ) e^(( q ) (r) K e (s))( t ) (u)` (v) (c) `( d ) (e) y=( f ) e^(( g ) (h) K(( i ) (j) x-2( k ))( l ))( m ) (n)` (o) (d) None of these
View SolutionSketch the region bounded by the curves `y=x^2a n dy=2/(1+x^2)` . Find the area.
View SolutionThe area enclosed between the curves `y=log_(e)(x+e),x=log_(e)((1)/(y))`, and the x-axis is
View SolutionFind the area of the region bounded by the curve C : y=tan x ,tangent drawn to C at x=pi/4, and the x-axis.
View SolutionFind all the possible values of `b >0,` so that the area of the bounded region enclosed between the parabolas `y=x-b x^2a n dy=(x^2)/b` is maximum.
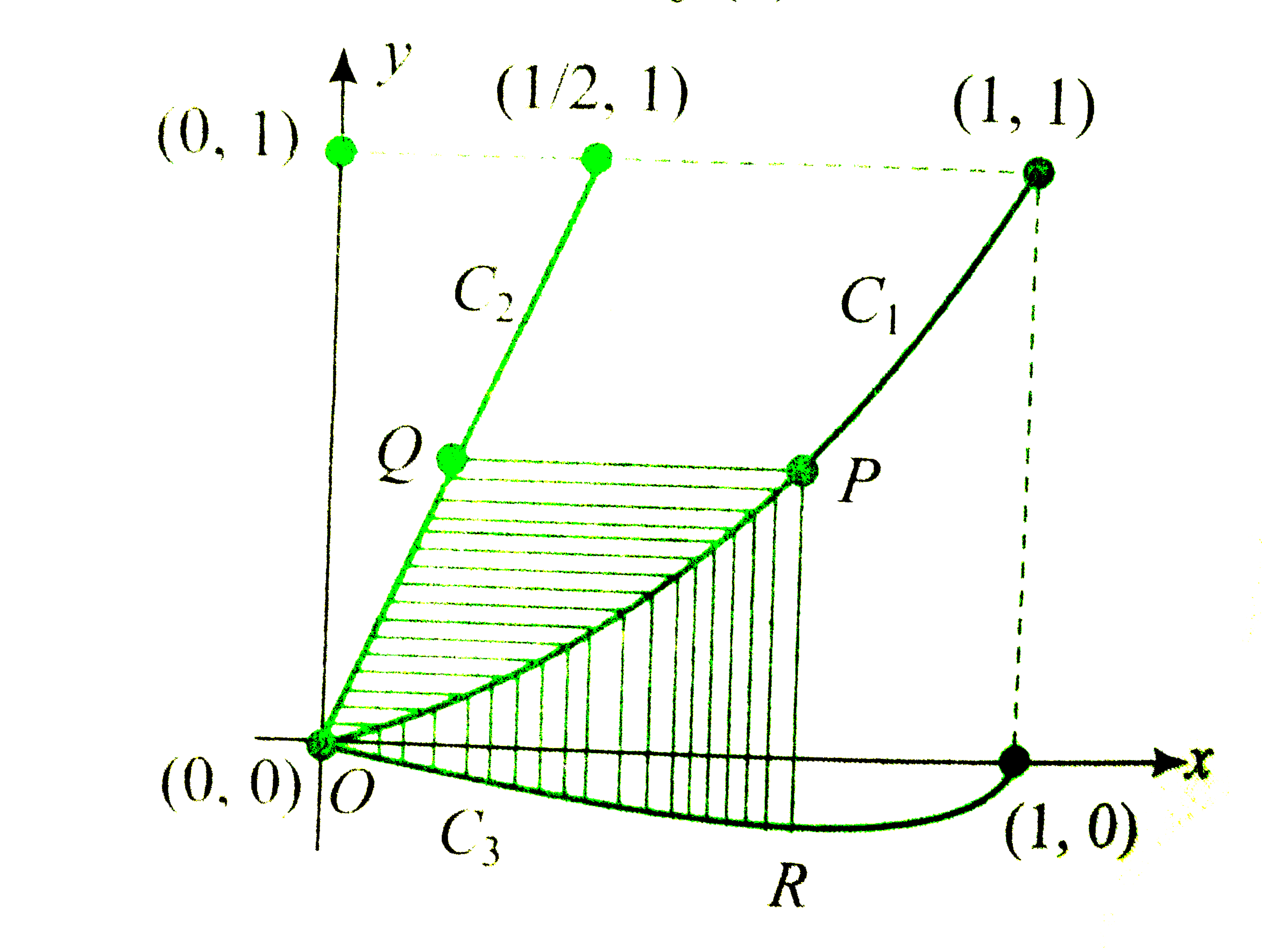
View SolutionLet `C_(1) and C_(2)` be the graphs of the functions `y=x^(2) and y=2x,` respectively, where `0le x le 1." Let "C_(3)` be the graph of a function y=f(x), where `0lexle1, f(0)=0.` For a point P on `C_(1),` let the lines through P, parallel to the axes, meet `C_(2) and C_(3)` at Q and R, respectively (see figure). If for every position of `P(on C_(1)),` the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
View SolutionCompute the area of the region bounded by the curves `y-e x(log)_e xa n dy=(logx)/(e x)`
View SolutionIf `A_n` be the area bounded by the curve `y=(tanx)^n` and the lines `x=0,\ y=0,\ x=pi//4` , then for `n > 2.`
View SolutionConsider a square with vertices at `(1, 1), (-1, 1), (-1, -1) and (1, -1)`. Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
View SolutionThe area of the region included between the curves `x^2+y^2=a^2 and sqrt|x|+sqrt|y|=sqrta(a > 0)` is
View SolutionShow that the area included between the parabolas `y^2 = 4a(x + a) and y^2 = 4b(b - x)` is `8/3 sqrt(ab) (a+b).`
View SolutionDetermine the area of the figure bounded by two branches of the curve `(y-x)^(2)=x^(3)` and the straight line `x=1`.
View SolutionProve that the areas `S_(0),S_(1),S_(2)`...bounded by the `x`-axis and half-waves of the curve `y=e^(-ax) sin betax,xge0` form a geometric progression with the common ratio `r=e^(-pi alpha//beta)`.
View SolutionLet `b!=0` and for `j=0,1,2,....,n`. Let `S_(j)` be the area of the region bounded by Y_axis and the curve `x cdot e^(ay)=sin by, (jpi)/bleyle((j+1)pi)/(b)`. Show that `S_(0),S_(1),S_(2),...S_(n)` are in geometric progression. Also, find their sum for a=-1 and `b=pi`.
View SolutionFor any real `t ,x=1/2(e^t+e^(-t)),y=1/2(e^t-e^(-t))` is a point on the hyperbola `x^2-y^2=1` Show that the area bounded by the hyperbola and the lines joining its centre to the points corresponding to `t_1a n d-t_1` is`t_1dot`
View SolutionFind the area enclosed by circle `x^(2)+y^(2)=4`, parabola `y=x^(2)+x+1`, the curve `y=[sin^(2)x/4+cos x/4]` and X-axis (where,[.] is the greatest integer function.
View SolutionLet `f(x)=M a xi mu m{x^2,(1-x)^2,2x(1-x)},` where `0lt=xlt=1.` Determine the area of the region bounded by the curves `y=f(x),x-a xi s ,x=0,` and `x=1.`
View SolutionLet `f(x)={(-2,-3 lex le0),(x-2,0 lt x le3):}`, where `g(x) = min {f(|x|)+|f(x)|, f(|x|)-|f(x)|}`. Find the area bounded by the curve `g(x)` and the X-axis between the ordinates at `x=3` and `x=-3`.
View SolutionLet `O(0,0),A(2,0),a n dB(1 1/(sqrt(3)))` be the vertices of a triangle. Let `R` be the region consisting of all those points `P` inside ` O A B` which satisfy `d(P , O A)lt=min[d(p ,O B),d(P ,A B)]` , where `d` denotes the distance from the point to the corresponding line. Sketch the region `R` and find its area.
View SolutionA curve `y=f(x)` passes through the origin. Through any point `(x , y)` on the curve, lines are drawn parallel to the co-ordinate axes. If the curve divides the area formed by these lines and co-ordinates axes in the ratio `m : n ,` find the curve.
View SolutionFind the ratio of the areas in which the curve `y=[(x^3)/(100)+x/35]` divides the circle `x^(2)+Y^(2)-4x+2y+1=0`. (where, [.] denotes the greated integer function).
View SolutionArea bounded by the line y=x, curve `y=f(x),(f(x)gtx,AA xgt1)` and the lines x=1,x=t is `(t-sqrt(1+t^2)-(1+sqrt2))` for all `tgt1`. Find `f(x)`.
View SolutionIf the area bounded by the curve y=f(x), x-axis and the ordinates x=1 and x=b is (b-1) `sin`(3b+4), then find f(x).
View SolutionLet f (x) be a function which satisfy the equatio `f (xy) = f9x) + f(y)` for all `x gt 0, y gt 0` such that `f '(1) =2.` Let A be the area of the region bounded by the curves `y =f (x), y = |x ^(3) -6x ^(2)+11 x-6| and x=0,` then find value of ` (28)/(17)A.`
View SolutionFind the area of the region which is inside the parabola satisfying the condition `|x-2 y|+|x+2y|le 8` and `xy ge 2`.
View SolutionConsider the function `f(x)={{:(x-[x]-(1)/(2),x !in),(0, "x inI):}` where [.] denotes the fractional integral function and I is the set of integers. Then find `g(x)max.[x^(2),f(x),|x|},-2lexle2.`
View SolutionFind the area of the region bounded by the curves `y=x^2 and y = sec^-1[-sin^2x],` where [.] denotes G.I.F.
View SolutionDraw a graph of the function `f(x) = cos^(-1) (4x^(3)-3x), x in [-1,1]` and find the ara enclosed between the graph of the function and the x-axis varies from 0 to 1.
View SolutionLet `f(x)` be continuous function given by `f(x)={2x ,|x|lt=1`and `x^2+a x+b ,|x|>1}dot`
Find the area of the region in the third quadrant bounded by the curves `x=-2y^2a n dy=f(x)` lying on the left of the line `8x+1=0.`
View SolutionLet `[x]` denotes the greatest integer function. Draw a rough sketch of the portions of the curves `x^(2)=4[sqrt(x)]y and y^(2)=4[sqrty]x` that lie within the square `{(x,y)|1lexle4, 1 leyle4}`. Find the area of the part of the square that is enclosed by the two curves and the line `x+y=3`.
View SolutionFind all the values of the parameter `a(ale1)` for which the area of the figure bounded by pair of straight lines `y^(2)-3y+2=0` and curves `y=[a]x^(2),y=1/2[a]x^(2)` is greatest , where [.] denotes the greatest integer function.
View SolutionFind the area in the 1* quadrant bounded by `[x]+[y]=n`, where `n in N and y=k`(where `k in n AA k<=n+1`), where [.] denotes the greatest integer less than or equal to x.
View Solution
Examples questions and complete solutions for chapter AREA OF BOUNDED REGIONS of ARIHANT MATHS (ENGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS AREA OF BOUNDED REGIONS
- Area of bounded Regions Exercise 5: Matching Type Questions
- Area of bounded Regions Exercise 7: Subjective Type Questions
- Examples
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Single Integer Answer Type Questions)
- Exercise (Single Option Correct Type Questions)
- Exercise (Statement I And Ii Type Questions)
- Exercise (Subjective Type Questions)
- Exercise For Session 1
- Exercise For Session 2