Complete Solutions to Example of chapter FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | FUNCTIONS |
| ARIHANT MATHS | Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
In the given figure, find the domain, codomain and range.

View SolutionThe number of functions `f: {1,2, 3,... n}-> {2016, 2017}`, where ne N, which satisfy thecondition f1)+f(2)+ ...+ f(n) is an odd number are
View SolutionFind whether `f(x)=x^(3)` forms a mapping or not.
View SolutionFind whether `x^(2)/a^(2)+y^(2)/b^(2)=1` forms a mapping or not.
View SolutionFind the domain of the following functions.
`{:((i)y=sqrt(5x-3),(ii)y=root(3)(5x-3)),((iii)y=(1)/((x-1)(x-2)),(iv)y=(1)/(root(3)(x-1))):}`
View SolutionFind the domain of `f(x)=sqrt(((1-5^x)/(7^(-1)-7)))`
View SolutionFind domain of the function `10^x+10^y=10`
View SolutionFind the domain of the function : `f(x)=1/(sqrt((log)_(1/2)(x^2-7x+13)))`
View SolutionFind domain of the function `f(x)=1/(log_10 (1-x)) +sqrt(x+2)`
View SolutionFind domain of `f(x)=log_(10)(1+x^(3))`.
View SolutionFind domain of `f(x)=log_(10)log_(10)(1+x^(3))`.
View SolutionFind domain of the function ` log_10 log_10 log_10 log_10 log_10 x`
View SolutionFind the domain of `f(x)=sqrt((log)_(0. 4)((x-1)/(x+5)))`
View SolutionFind the domain `f(x)=log_(100x)((2 log_(10) x+1)/-x)`
View SolutionThe domain of definition of `f(x)=((log)_2(x+3))/(x^2+3x+2)` is `R-{-1,-2}` (b) `-2,oo)` `R-{-1,-2,-3}` (d) `(-3,oo)-{-1,-2}`
View SolutionFind the domain for `f(x)=sin^(-1)((x^(2))/(2))`.
View SolutionThe domain of definition of the function
`f(x)= sin^(-1){log_(2)((x^(2))/(2))}`, is
View SolutionFind domain for `f(x)=sqrt(cos (sin x))`
View SolutionFind the domain for `f(x)=sin^(-1)((1+x^2)/(2x))`
View SolutionFind range and domain of `f(x)=sqrt(s i n^-1(log_2x))`
View SolutionThe domain of the function
`f(x)=log_(e){log_(|sinx|)(x^(2)-8x+23)-(3)/(log_(2)|sinx|)}`
contains which of the following interval (s) ?
View SolutionSolve for x.
`abs(x-3)+abs(4-x)=1`
View SolutionSolve `abs(x/(x-1))+abs(x)=x^(2)/abs(x-1)`.
View SolutionFind domain for `y=1/sqrt(abs(x)-x)`.
View SolutionThe domain of the function `f(x)=1/(sqrt(4x=|x^2-10 x+9}))` is `(7-sqrt(40),7+sqrt(40))` `(0,7+sqrt(40))` `(7-sqrt(40),oo)` (d) none of these
View SolutionThe domain of the function
`f(x)=sqrt(abs(sin^(-1)(sinx))-cos^(-1)(cosx))` in `[0,2pi]` is
View SolutionSketch the graph of
`{:((i) f(x)=sgn(x^(2)+1),(ii) f(x)=sgn(log_(e)x)),((iii) f(x)=sgn(sin x), (iv) f(x)=sgn(cos x)):}`
View SolutionFind domain for, `f(x)=cos^(-1)[x]`.
View SolutionFind the value of
`[3/4]+[3/4+1/100]+[3/4+2/100]+...+[3/4+99/100]`.
View SolutionGiven that `y=2[x]+3` and `y=3[x-2]+5` then find the value of `[x+y]`
View SolutionFind domain for `f(x)=[sinx] cos(pi/([x-1]))`.
View SolutionThe domain of the function
`f(x)=(log_(4)(5-[x-1]-[x]^(2)))/(x^(2)+x-2)` is
(where [x] denotes greatest integer function)
View Solution`f(x)= 1/sqrt([x]-x)`, where `[*]` denotes the greatest integeral function less than or equals to x. Then, find the domain of f(x).
View SolutionThe function `f(x)` is defined in `[0,1]` . Find the domain of `f(t a nx)dot`
View SolutionIf the domain of `y=f(x)` is `[-3,2]`, then find the domain of `g(x)=f([x]),` where [] denotes the greatest integer function.
View SolutionIf the function f(x)=[3.5+bsin x] (where [.] denotes the greatest integer function) is an even function, the complete set of values of b is
View SolutionThe domain of the function
`f(x)=log_(3)log_(1//3)(x^(2)+10x+25)+(1)/([x]+5)`
(where [.] denotes the greatest integer function) is
View SolutionIf [x] dnote the greatest integer less than or equal to x then the equation ` sin x=[1+sin x ]+[1-cos x ][` has no solution in
View SolutionIf `{x}` and `[x]` represent fractional and integral part of x respectively, find the value of `[x]+sum_(r=1)^(2000)({x+r})/2000`
View SolutionSolve the equation `4[x]=x+{x}`
View SolutionFind the solution set of `(x)^(2)+(x+1)^(2)=25` where `(x)` is the least integer greater than or equal to `x`.
View SolutionIf `[x]` is the greatest integer less than or equal to `x` and `(x)` be the least integer greater than or equal to `x` and `[x]^(2)+(x)^(2)gt25` then `x` belongs to
View SolutionThe number of solutions of `|[x]-2x|=43`, where `[x]` denotes the greatest integer `lex` is
View SolutionFind the range for `y=(x-[x])/(1-[x]+x)`.
View SolutionFind the range for `f(x)=e^(x)/(1+[x]) " when " x ge 0`.
View SolutionFind the domain and range of the function `y=log_(e)(3x^(2)-4x+5)`.
View SolutionFind the range of `f(x) = sqrt( x- 1) + sqrt(5 - x)`.
View SolutionFind the range of `log_3{log_(1/2)(x^2+4x+4)}`
View SolutionRange of the function
`f(x)=(cos^(-1)abs(1-x^(2)))` is
View SolutionIf `x,y` and`z` are three real numbers such that `x+y+z=4` and `x^2+y^2+z^2=6`,then show that each of x,y and z lie in the closed interval `[2/3,2]`
View SolutionThe range of the function
`f(x)=1/abs(sinx)+1/abs(cosx)` is
View SolutionIf `z=x+i ya n dx^2+y^2=16 ,` then the range of `||x|-|y||` is `[0,4]` b. `[0,2]` c. `[2,4]` d. none of these
View SolutionFind the range of f(x)=`(1)/(pi)sin^(-1)x+tan^(-1)+(x+1)/(x^(2)+2x+5)`
View SolutionThe range of the function `sin^2x-5sinx -6` is
View SolutionRange of the function
`f(x)=sqrt(abs(sin^(-1)abs(sinx))-abs(cos^(-1)abs(cosx)))` is
View SolutionThe number of values of `yin[-2pi,2pi]` satisfying the equation `|sin2x|+|cos2x|=|siny|` is 3 (b) 4 (c) 5 (d) 6
View Solution`f(x)=cot^(- 1)(x^2-4x+5)` then range of `f(x)` is equal to :
View SolutionFind the range of `f(x)=(x^(2)+14x+9)/(x^(2)+2x+3)`, where x `in` R.
View SolutionIf the range of function ` f(x) = (x + 1)/(k+x^(2))` contains the interval
[-0,1] , then values of k can be equal to
View SolutionFind the range of the function
`" " f(x)=(sin^(2)x+sinx-1)/(sin^(2)x-sinx+2)`.
View SolutionIf f is an even function, then find the realvalues of x satisfying the equation `f(x)=f((x+1)/(x+2))`
View SolutionFind out whether the given function is even, odd or neither even nor odd
`" where " f(x)={{:(xabs(x),",",x le -1),([1+x]+[1-x],",",-1 lt x lt 1),(-xabs(x),",",x ge 1 ):}`
where `||` and [] represent then modulus and greater integer functions.
View SolutionProve sin x is periodic and find its period.
View SolutionProve that f(x)=x-[x] is periodic function. Also, find its period.
View SolutionLet `f(x)` be periodic and `k` be a positive real number such that `f(x+k)+f(x)=0fora l lx in Rdot` Prove that `f(x)` is periodic with period `2kdot`
View SolutionFind periods for
`{:((i) cos^(4)x., (ii) sin^(3)x., (iii)cos sqrt(x).,(iv) cos x.):}`
View SolutionFind the period `f(x)=sinx+{x},` where {x} is the fractional part of `xdot`
View SolutionFind period of `f(x)=tan3x+sin(x/3)`.
View SolutionFind the period of `f(x)=sinx+tanx/2+sinx/(2^2)+t a n x/(2^3)+....+sinx/(2^(n-1))+tanx/(2^n)`
View SolutionFind the period of `f(x)=abs(sinx)+abs(cosx)`.
View SolutionPeriod of` f(x) = sin^4 x + cos^4 x`
View SolutionFind the period of `"cos"(cosx)+cos(sinx)dot`
View SolutionFind the period of `f(x)=cos^(-1)(cos x)`
View SolutionThe period of `f(x)=cos(abs(sinx)-abs(cosx))` is
View SolutionPeriod of the function `f(x)=sin(sin(pix))+e^({3x})`, where {.} denotes the fractional part of x is
View SolutionLet `f(x)=sinx+cos(sqrt(4-a^(2)))x`. Then, the integral values of 'a' for which f(x) is a periodic function, are given by
View SolutionLet`f(x)={{:(-1+sinK_(1)pix",", "x is rational."), (1+cosK_(2)pix",", x):}`
If f(x) is a periodic function, then
View SolutionIf `f(x)=tan^2((pix)/(n^2-5n+8))+cot(n+m)pix;(n in N, m in Q)` is a periodic function with 2 as its fundamental period, then m can't belong to
View SolutionLet `f(x)` be a periodic function with period `int_0^x f(t+n) dt 3 and f(-2/3)=7 and g(x) =` .where `n=3k, k in N`. Then `g'(7/3) =`
View SolutionLet `f:[-pi//2,pi//2] rarr [-1,1]` where f(x)=sinx. Find whether f(x) is one-one or not.
View SolutionIf `f(x)=x^3+3x^2+4x+ bsinx+ c cosx AA x in R` is a one-one function then the value of `b^2 + c^2` is
View SolutionShow `f:R rarr R " defined by " f(x)=x^(2)+x " for all " x in R` is many-one.
View SolutionShow that `f: R->R` defined by `f(x)=(x-1)(x-2)(x-3)` is surjective but not injective.
View SolutionIf `f:R rarr [pi/6,pi/2], f(x)=sin^(-1)((x^(2)-a)/(x^(2)+1))` is an onto function, the set of values `a` is
View SolutionShow `f:R rarr R` defined by `f(x)=x^(2)+4x+5` is into
View SolutionLet `A={x:-1 le x le 1}=B` be a function `f: A to B.` Then find the nature of each of the following functions.
(i) `f(x) = |x| " (ii) " f(x)=x|x|`
(iii) `f(x)=x^(3) " (iv) " f(x)="sin"(pi x)/(2)`
View SolutionThe function `f : R -> R` defined as `f (x) =1/2 In (sqrt(sqrt(x^2+1)+x) + sqrt(sqrt(x^2+1)-x))` is
View SolutionIf X={1,2,3,4,5} and Y={a,b,c,d,e,f} and `f:X rarr Y`, find the total number of
`{:((i)" functions ",(ii)" one to one functions "),((iii)" many-one functions ",(iv)" constant functions "),((v)" onto functions ",(vi)" into functions "):}`
View SolutionFind the number of surjections from A to B, where A={1,2,3,4}, B={a,b}.
View Solution`f(x)=log_(x^(2)) 25 and g(x)=log_(x)5.` Then f(x)=g(x) holds for x belonging to
View SolutionLet `A={1,2},\ B={3,6}` and `f: A->B` given by `f(x)=x^2+2\ n d\ g: A->B` given by `g(x)=3xdot` Then we observe that `f\ a n d\ g` have the same domain and co-domain. Also we hve, `f(1)=3=g(1)a n d\ f(2)=6=g(2)dot` Hence `f=gdot`
View SolutionWhich pair of functions is identical?
View SolutionLet `f: A -> B and g : B -> C` be two functions and `gof: A -> C` is define statement(s) is true?
View SolutionLet `R` be the set of real numbes. If `f: RvecR ;f(x)=x^2` and `g: RvecR ;g(x)=2x+1` . Then, find `foga n dgof` . Also, show that `fog!=gofdot`
View SolutionLet g(x)=1+x-[x]
`"and " f(x)={{:(-1","x lt 0),(0","x=0),(1","x gt 0):}`
Then, for all x, find f(g(x)).
View SolutionLet `f (x) [ {:(1+x"," , 0 le x le 2),( 3-x"," ,2 lt x le 3):}:`
` g(x) =f (f (x)):`
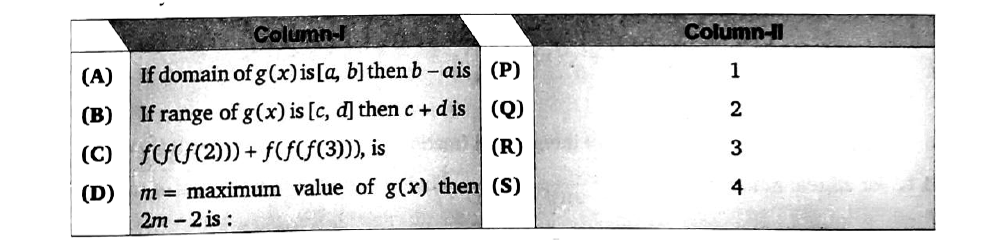
View SolutionLet `f(x)={(x+1",", x lt1),(2x+1",",1lt x le 2):}" and " g(x)={(x^(3)",", -1 le x lt 2),(x+2",",2 le x le 3):}`
find `fog(x)`.
View SolutionIf `f(x)=2x+abs(x),g(x)=1/3(2x-abs(x))` and h(x)=f(g(x)), domain of `underbrace(sin^(-1)(h(h(h(h...h(x)...)))))_("n times")` is
View SolutionA function `f: RvecR` satisfies `xcosy(f(2x+2y)-f(2x-2y)=cosxsiny(f(2x+2y)+f(2x-2y))dot` If `f^(prime)(0)=1/2,t h e n` `a)f^(prime)(x)=f(x)=0` `b)4f^(x)+f(x)=0` `c)f^(x)+f(x)=0` `d)4f^(x)-f(x)=0`
View SolutionIf `f(x)=3x-5,` then `f^(-1)(x)` is given by `1/((3x-5))` is given by `((x+5))/3` does not exist because `f` is not one-one does not exist because `f` is not onto
View Solution
Example questions and complete solutions for chapter FUNCTIONS of ARIHANT MATHS (ENGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS FUNCTIONS
- Example
- Exercise (Matching Type Questions)
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Single Integer Answer Type Questions)
- Exercise (Single Option Correct Type Questions)
- Exercise (Statement I And Ii Type Questions)
- Exercise (Subjective Type Questions)
- Exercise For Session 1
- Exercise For Session 10
- Exercise For Session 11
- Exercise For Session 12
- Exercise For Session 2
- Exercise For Session 3
- Exercise For Session 4
- Exercise For Session 5
- Exercise For Session 6
- Exercise For Session 7
- Exercise For Session 8
- Exercise For Session 9
- FUNCTION EXERCISE 5: Matching Type Questions
- FUNCTION EXERCISE 7: Subjective Type Questions
- FUNCTION EXERCISE 8:Questions Asked in Previous 10 Years Exams