Complete Solutions to Exercise (More Than One Correct Option Type Questions) of chapter LIMITS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | LIMITS |
| ARIHANT MATHS | Exercise (More Than One Correct Option Type Questions) |
| Number Of Questions | 15 |
| Academic Year | 2023-24 |
If `lim_(x -> oo) 4x ( pi/4 - tan^-1 ((x+1) / (x+2))) = y^2 + 4y + 5` then `y` can be equal to
View Solution`lim_(xto0)(1-cos(x^(2)))/(x^(3)(4^(x)-1))` is equal to:
View SolutionIf `f(x)=e^([cotx])`, where `[y]` represents the greatest integer less than or equal to `y` then
View Solution`lim_(xto0)[m(sinx)/x]` is equal to (where `m epsilon I` and `[.]` denotes greatest integer function)
View SolutionIf `("lim")_(xvec0)(1+a x+b x^2)^(2/x)=e^3,` then find the value of `aa n dbdot`
View SolutionThe graph of the function `y=f(x)` is shown in the adjacent figure then correct statement is
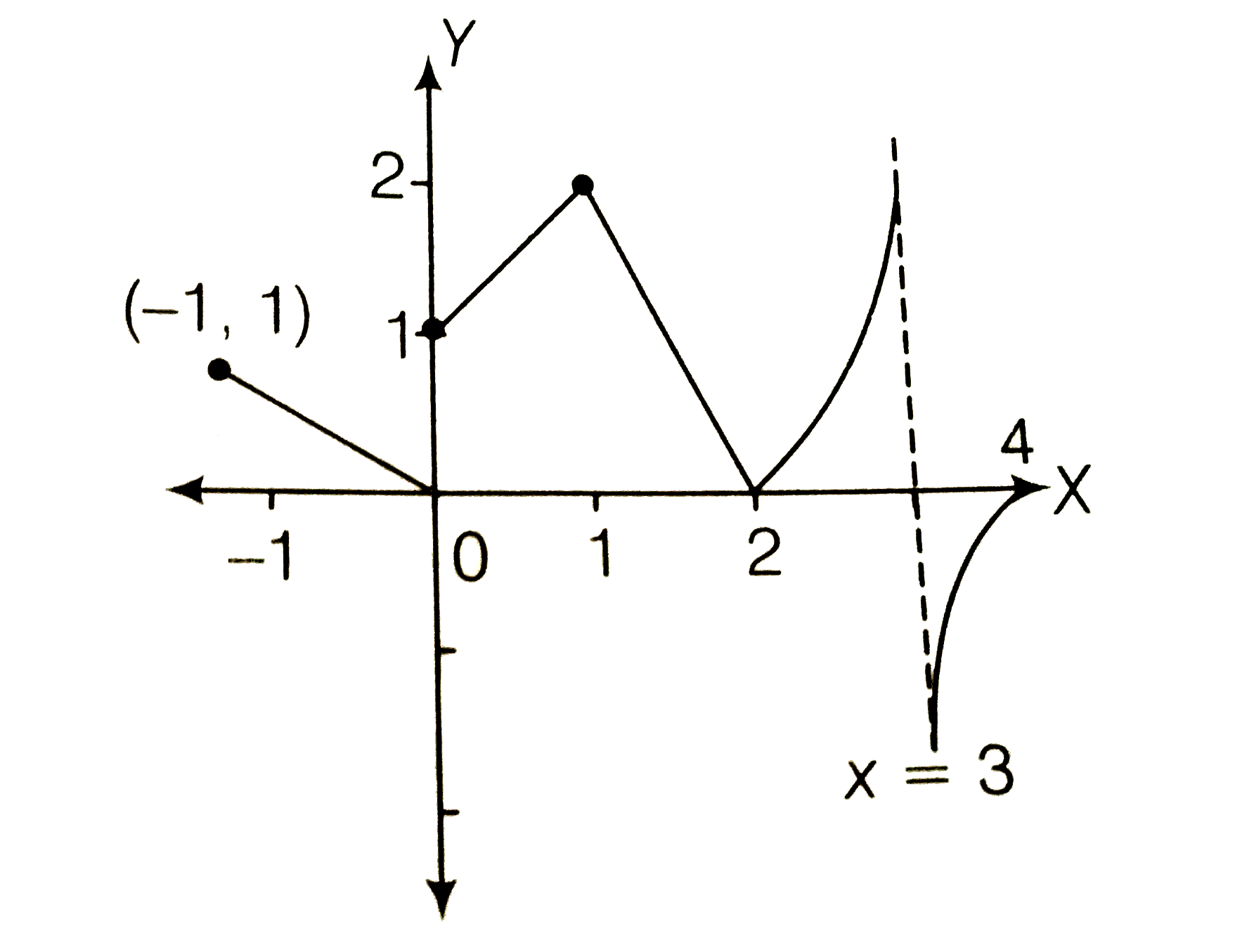
View SolutionFind `lim_(xto0)(cot^(-1)(1/x))/x`
View SolutionIf `l=lim_(xtooo)((x+1)/(x-1))^(x)`, the value of `{l}` and `[l]` are
View SolutionIf `f(x)={("sin"[x])/([x]),for[x]!=0, 0,for[x]=0,w h e r e[x]` denotes the greatest integer less than or equal to `x ,` then `("lim")_(xvec0)f(x)` is (a) `1` (b) 0 (c) `-1` (d) none of these
View Solution`lim_(xtoc)f(x)` does not exist when
where `[.]` and `{.}` denotes greatest integer and fractional part of `x`
View SolutionIdentify the correct statement.
View SolutionFor `agt0,` let `l=lim_(xto(pi)/2)(a^(cotx)-a^(cosx))/(cotx-cosx)` and `m=lim_(xto-oo)(sqrt(x^(2)+ax))-(sqrt(x^(2)-ax))` then solve it
View SolutionConsider the function `f(x)=((ax+1)/(bx+2))^(x)`, where `a,bgt0`, the `lim_(xtooo)f(x)` is
View SolutionIf `f(x)=(x.2^(x)-x)/(1-cosx)` and `g(x)=2^(x).sin((log2)/(2^(x)))` then
View SolutionIf `lim_(xto3)(x^(3)+cx^(2)+5x+12)/(x^(2)-7x+12)=l` (finite real number), ten
View Solution
Exercise (More Than One Correct Option Type Questions) questions and complete solutions for chapter LIMITS of ARIHANT MATHS (ENGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS LIMITS
- Examples
- Exercise (Matching Type Questions)
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Single Integer Answer Type Questions)
- Exercise (Single Option Correct Type Questions)
- Exercise For Session 1
- Exercise For Session 2
- Exercise For Session 3
- Exercise For Session 4
- Exercise For Session 5
- Exercise For Session 6
- MATCHING TYPE QUESTIONS