Complete Solutions to Exercise (Passage Based Questions) of chapter LIMITS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | LIMITS |
| ARIHANT MATHS | Exercise (Passage Based Questions) |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
If `lim_(xtoa)f(x)=1` and `lim_(xtoa)g(x)=oo` then `lim_(xtoa){f(x)}^(g(x))=e^(lim_(xtoa)(f(x)-1)g(x))`
`lim_(xto0)((sinx)/x)^((sinx)/(x-sinx))` is equal to
View SolutionIf `lim_(xtoa)f(x)=1` and `lim_(xtoa)g(x)=oo` then `lim_(xtoa){f(x)}^(g(x))=e^(lim_(xtoa)(f(x)-1)g(x))` `lim_(xto0)((x-1+cosx)/x)^(1/x)` is equal to
View SolutionIf `lim_(xtoa)f(x)=1` and `lim_(xtoa)g(x)=oo` then `lim_(xtoa){f(x)}^(g(x))=e^(lim_(xtoa)(f(x)-1)g(x))` `lim_(xto0)((a^(x)+b^(x)+c^(x))/3)^(2/x)` is equal to
View SolutionFind `dy/dx if 2x-3y=tanx`
View SolutionFind |A| If `A = |(x^2, 2x), (x^4 , 5x)|`
View SolutionLet `f(x)=lim_(ntooo)(cos sqrt(x/n))^(n),g(x)=lim_(nto oo)(1-x+x root(n)(e))^(n)`
Now consider the function `y=h(x)` where `h(x)=tan^(-1)(g^(-1)f^(-1)(x))`.
Range of the function `y=h(x)` is
View SolutionHow many 4 digits numbers can be formed from the digits 1 to 10 if not digit can be repeated.
View SolutionFind `dy/dx if 2y=e^y-2x`
View SolutionLet `f: N -> R and g : N -> R` be two functions and `f(1)=08, g(1)=0.6`, `f(n+1)=f(n)cos(g(n))-g(n)sin(g(n)) and g (n+1)=f(n) sin(g(n))+g(n) cos(g(n))` for `n>=1`. `lim_(n->oo) f(n)` is equal to
View SolutionLet `f:NtoR` and `g:NtoR` be two functions and `f(1)=0.8,g(1)=0.6,f(n+1)=f(n) cos (g(n))-g(n)sin(g(n))` and `g(n+1)=f(n)sin(g(n))+g(n)cos(g(n))` for `n ge1`.
`lim_(ntooo)f(n)` is equal to
View SolutionA circle arc of radius `1` subtends an angle of `x` radians as shown in figure. The centre of the circle is `O` and the point `C` is the intersection of two tangent lines at `A` and `B`. Let `T(x)` be the area of `DeltaABC` and `S(x)` be the area of shaded region.
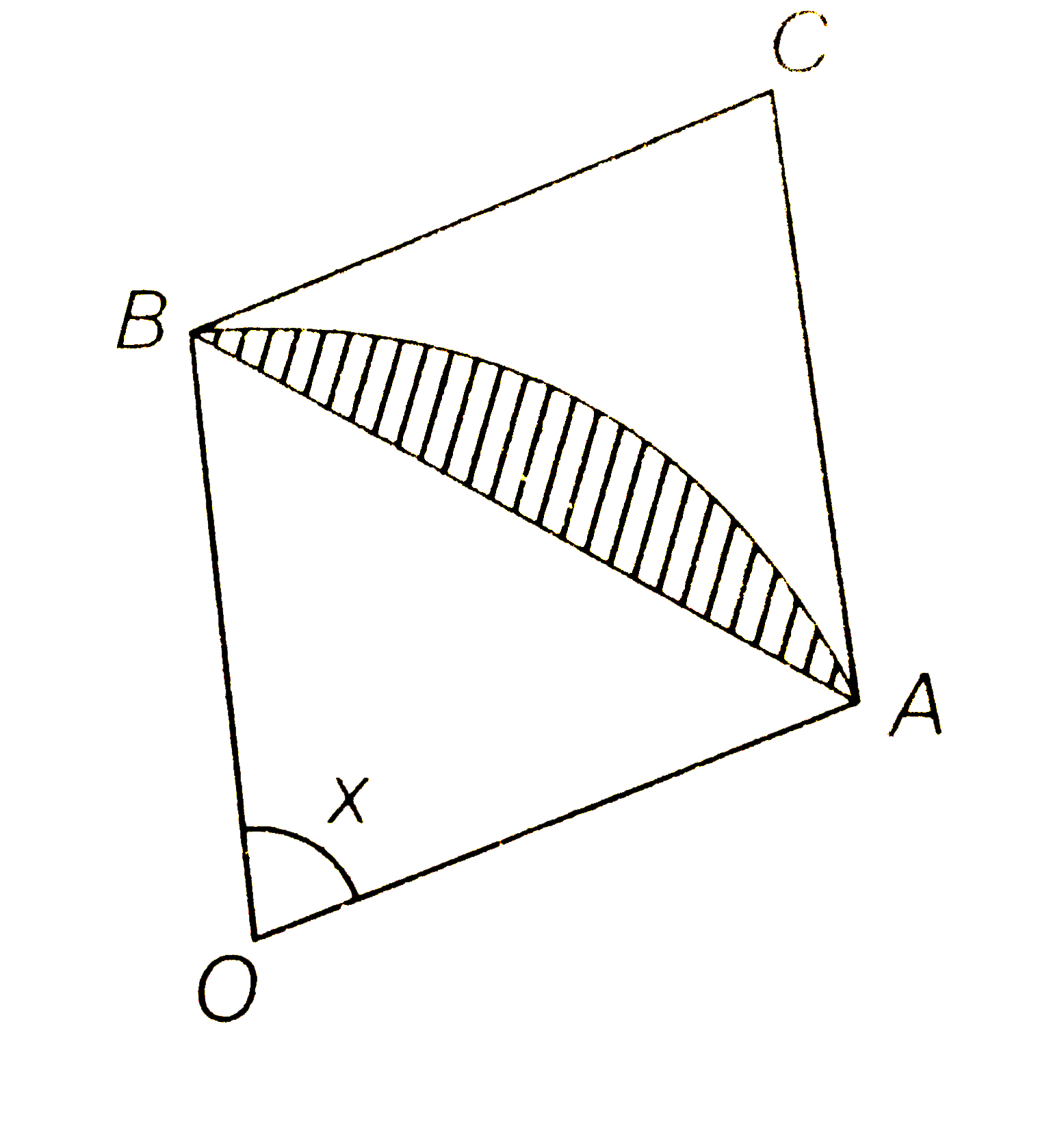
`lim_(xto0)(T(x))/(x^(3))` is
View SolutionA circle arc of radius 1 subtends an angle of x radians as shown in figure. The centre of the circle is O and the point C is the intersection of two tangent lines at A and B. Let `T(x)` be the area of `DeltaABC` and `S(x)` be the area of shaded region.
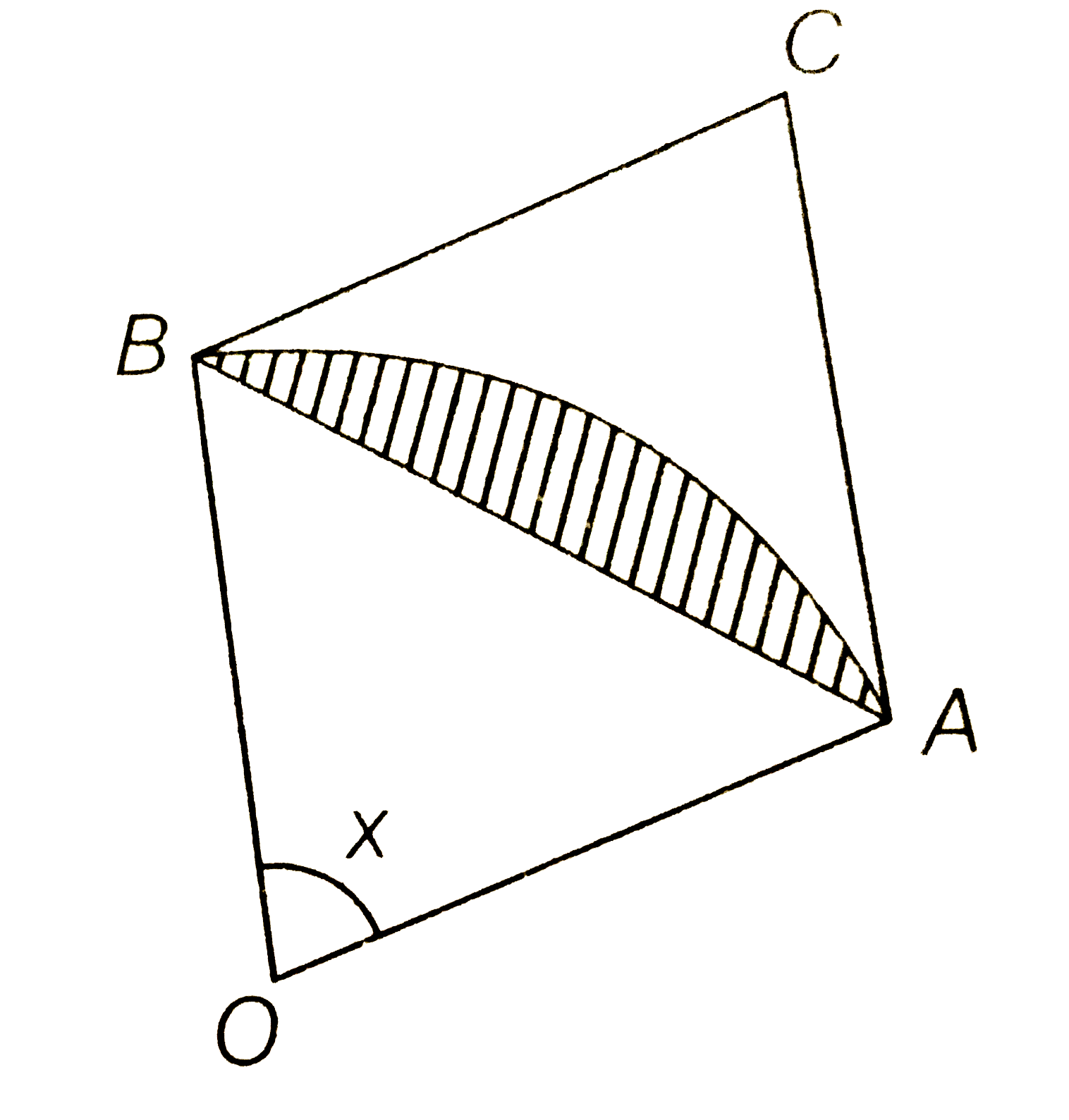
`lim_(xto0)(S(x))/x` is
View SolutionA circular are of radius `1` subtends an angle of `x` radians `0 < x < pi/2` as shown in the figure . the point `r` is the intersection of the two tangent line at `P` and `Q`. let `T(x)` be the area of triangle `PQR` and `S(x)` be the area of the shaded region then find `T(x) & S(x) & lim_(x->0)(T(x))/(S(x))`
View Solution
Exercise (Passage Based Questions) questions and complete solutions for chapter LIMITS of ARIHANT MATHS (ENGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS LIMITS
- Examples
- Exercise (Matching Type Questions)
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Single Integer Answer Type Questions)
- Exercise (Single Option Correct Type Questions)
- Exercise For Session 1
- Exercise For Session 2
- Exercise For Session 3
- Exercise For Session 4
- Exercise For Session 5
- Exercise For Session 6
- MATCHING TYPE QUESTIONS