Complete Solutions to Exercise (Single Option Correct Type Questions) of chapter DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS |
| ARIHANT MATHS | Exercise (Single Option Correct Type Questions) |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
Consider the cubic equation `f(x)=x^(3)-nx+1=0` where `n ge3, n in N` then `f(x)=0` has
07:23View SolutionIf the normal to `y=f(x)` at (0, 0) is given by `y-x =0,` then `lim_(x to 0)(x^(2))/(f(x^(2))-20f(9x^(2))+2f(99x^(2)))`, is
07:09View SolutionTangent to a curve intercepts the y-axis at a point P. A line perpendicular to the tangent through P passes through another point (1,0). The differential equation of the curve is
02:55View SolutionThe number of point in the rectangle `{(x , y)}-12lt=xlt=12a n d-3lt=ylt=3}` which lie on the curve `y=x+sinx` and at which in the tangent to the curve is parallel to the x-axis is (a) 0 (b) 2 (c) 4 (d) 8
03:32View SolutionIf `3(a+2c)=4(b+3d),` then the equation `a x^3+b x^2+c x+d=0` will have no real solution at least one real root in `(-1,0)` at least one real root in `(0,1)` none of these
04:51View SolutionIf `3(a+2c)=4(b+3d),` then the equation `a x^3+b x^2+c x+d=0` will have no real solution at least one real root in `(-1,0)` at least one real root in `(0,1)` none of these
04:51View SolutionLet f(x) be a differentiable function in the interval (0, 2) then the value of `int_(0)^(2)f(x)dx`
03:04View SolutionLet `f(x)` be a fourth differentiable function such `f(2x^2-1)=2xf(x)AA x in R,` then `f^(iv)(0)` is equal
02:18View SolutionThe curve `x+y-log_(e)(x+y)=2x+5` has a vertical tangent at the point `(alpha, beta).` then `alpha+beta` is equal to
03:16View SolutionLet y = f(x), `f : R ->R` be an odd differentiable function such that `f'''(x)>0` and `g(alpha,beta)=sin^8alpha+cos^8beta+2-4sin^2alpha cos^2 beta` If `f''(g(alpha, beta))=0` then `sin^2alpha+sin^2beta` is equal to
07:37View SolutionA polynomial of 6th degree `f(x)` satisfies `f(x)=f(2-x), AA x in R`, if `f(x)=0` has 4 distinct and 2 equal roots, then sum of the roots of `f(x)=0` is
05:56View SolutionLet a curve `y=f(x),f(x)ge0, AA x in R` has property that for every point P on the curve length of subnormal is equal to abscissa of p. If `f(1)=3`, then f(4) is equal to
03:03View SolutionIf a variable tangent to the curve `x^2y=c^3` makes intercepts `a , bonx-a n dy-a x e s ,` respectively, then the value of `a^2b` is `27c^3` (b) `4/(27)c^3` (c) `(27)/4c^3` (d) `4/9c^3`
08:59View SolutionLet `f(x)=|(1,1,1),(3x-x,5-3x^(2),3x^(3)-1),(2x^(2)-1,3x^(5)-1,7x^(8)-1)|`. Then which of the following is/are correct?
07:39View SolutionThe graphs `y=2x^(3)-4x+2and y=x^(3)+2x-1` intersect in exactly 3 distinct points. Then find the slope of the line passing through two of these points.
04:01View SolutionIn which of the following functions is Rolles theorem applicable? `(a)f(x)={x ,0lt=x<1 0,x=1on[0,1]` `(b)f(x)={(sinx)/x ,-pilt=x<0 0,x=0on[-pi,0)` `(c)f(x)=(x^2-x-6)/(x-1)on[-2,3]` `(d)f(x)={(x^3-2x^2-5x+6)/(x-1)ifx!=1,-6ifx=1on[-2,3]`
10:06View SolutionThe figure shows a right triangle with its hypotenuse `OB` along the `y`-axis and its vertex `A` on the parabola `y=x^(2)`.
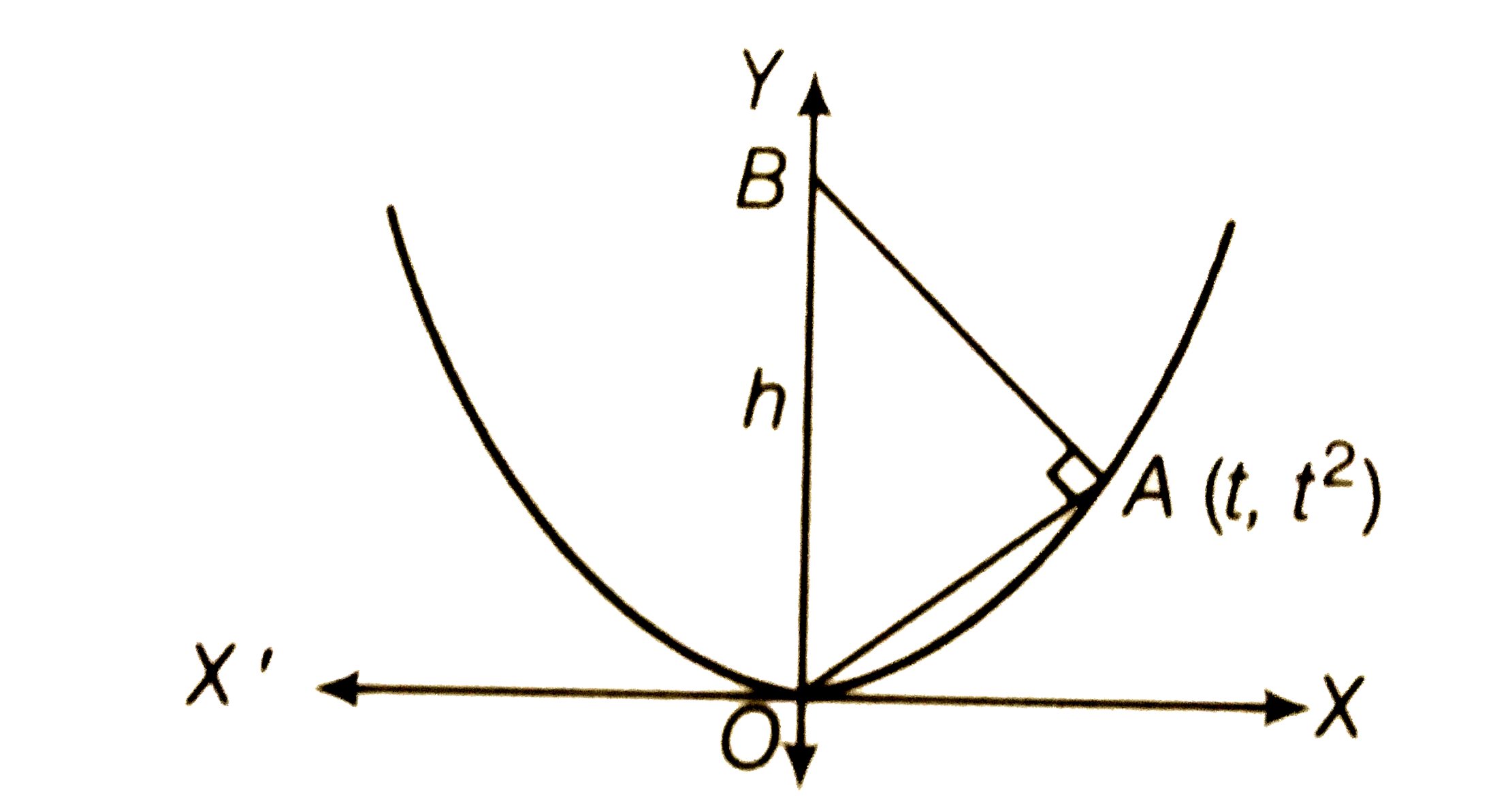
Let `h` represents the length of the hypotenuse which depends on the `x`-coordinate of the point `A`. The value of `lim_(t to o (h)` is equal to02:43View SolutionNumber of positive integral value(s) of `a` for which the curve `y=a^(x)` intersects the line `y=x` is:
02:58View SolutionGiven `f(x)=4-(1/2-x)^(2/3),g(x)={("tan"[x])/x ,x!=0 1,x=0` `h(x)={x},k(x)=5^((log)_2(x+3))` Then in [0,1], lagranges mean value theorem is not applicable to (where [.] and {.} represents the greatest integer functions and fractional part functions, respectively). `f` (b) `g` (c) `k` (d) `h`
17:00View SolutionIf the function `f(x)=x^(4)+bx^(2)+8x+1` has a horizontal tangent and a point of inflection for the same value of x, then the value of b is equal to
02:25View SolutionCoffee is coming out from a conical filter, with height and diameter both are 15 cm into a cylindrical coffee pot with a diameter 15 cm. The rate at which coffee comes out from the filter into the pot is 100 cu cm/min.
The rate (in cm/min) at which the level in the pot is rising at the instance when the coffe in the pot is 10 cm, is04:06View SolutionA horse runs along a circle with a speed of `20k m//h` . A lantern is at the centre of the circle. A fence is along the tangent to the circle at the point at which the horse starts. Find the speed with which the shadow of the horse moves along the fence at the moment when it covers 1/8 of the circle in km/h.
06:52View SolutionWater runs into an inverted conical tent at the rate of `20 ft^3`/ min and leaks out at the rate of `5 ft^3`/min .The height of the water is three times the radius of the water's surface. The radius of the water surface is increasing when the radius is 5 ft, is
03:21View SolutionLet `f(x)=x^3-3x^2+2x` Find `f'(x)`
01:00View SolutionThe x-intercept of the tangent at any arbitrary point of the curve `a/(x^2)+b/(y^2)=1` is proportional to square of the abscissa of the point of tangency square root of the abscissa of the point of tangency cube of the abscissa of the point of tangency cube root of the abscissa of the point of tangency
05:13View SolutionIf f(x) is continuous and differentible over `[-2, 5]` and `-4lef'(x)le3` for all x in `(-2, 5)`, then the greatest possible value of `f(5)-f(-2)` is
03:02View SolutionA curve is represented parametrically by the equations `x=t+e^(at) and y=-t +e^(at, t in R and a gt 0`. If the curve touches the axis of x at the point A, then the coordinates of the point A are
03:40View SolutionAt any two points of the curve represented parametrically by `x=a (2 cos t- cos 2t);y = a (2 sin t - sin 2t)` the tangents are parallel to the axis of x corresponding to the values of the parameter t differing from each other by :
05:18View SolutionLet `F(x)=int_(sinx)^(cosx)e^((1+sin^(-1)(t))dt` on `[0,(pi)/(2)]`, then
05:12View SolutionGiven `f'(1)=1and f(2x)=f(x)AAxgt0.If f'(x)` is differentiable, then there exists a number `c in (2,4)` such that `f''(c )` equal
03:26View SolutionLet `f(x)a n dg(x)` be two functions which are defined and differentiable for all `xgeqx_0dot` If `f(x_0)=g(x_0)a n df^(prime)(x)>g^(prime)(x)` for all `x > x_0,` then prove that `f(x)>g(x)` for all `x > x_0dot`
02:07View SolutionThe range of values of m for which the line y = mx and the curve `y=(x)/(x^(2)+1)` enclose a region, is
01:54View SolutionLet S be a square with sides of length x. If we approximate the change in size of the area of S by `h (dA)/(dx)|_(x=x_0)`, when the sides are changed from `x_0` to `x_0 + h`, then the absolute value of the error in our approximation, is
02:53View SolutionConsider `f(x)=int_1^x(t+1/t)dt` and `g(x)=f'(x)` If P is a point on the curve `y=g(x)` such that the tangent to this curve at P is parallel to the chord joining the point `(1/2,g(1/2))` and `(3,g(3))` of the curve then the coordinates of the point P
06:55View Solution
Exercise (Single Option Correct Type Questions) questions and complete solutions for chapter DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS of ARIHANT MATHS (ENGLISH) of Class 12
All Exercises from ARIHANT MATHS Class 12 MATHS DY / DX AS A RATE MEASURER AND TANGENTS, NORMALS
- EXAMPLE
- Examples
- Exercise (Matching Type Questions)
- Exercise (More Than One Correct Option Type Questions)
- Exercise (Passage Based Questions)
- Exercise (Questions Asked In Previous 13 Years Exam)
- Exercise (Single Integer Answer Type Questions)
- Exercise (Single Option Correct Type Questions)
- Exercise (Statement I And Ii Type Questions)
- Exercise (Subjective Type Questions)
- EXERCISE : 5
- Exercise For Session 1
- Exercise For Session 2
- Exercise For Session 3
- Exercise For Session 4
- Exercise For Session 5
- Exercise For Session 6
- SINGLE OPTION CORRECT TYPE QUESTIONS
