Complete Solutions to बहुविकल्पीय प्रश्न of chapter रैखिक प्रोग्रामन of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | रैखिक प्रोग्रामन |
| BALAJI PUBLICATION | बहुविकल्पीय प्रश्न |
| Number Of Questions | 13 |
| Academic Year | 2023-24 |
रैखिक प्रोग्रामन समस्या निम्न व्यवरोधों के अन्तर्गत `x_(1) + 2x_(2) le 2000, x_(1) + x_(2) le 1500 , x_(2) le 600` और `x_(1) , x_(2) ge 0` हैं तो कौन - सा बिंदु घिरा हुए धन भाग में नही हैं ?
View Solutionनिम्न व्यवरोधों `x+2y ge 11, 3x+4y ge 30, 2x + 5y le 30, xge0, yge0` के अन्तर्गत कौन - सा बिंदु इसके अन्तर्गत होगा ?
View Solutionअसमिका `2x + y ge 2` तथा `x - y le 3` के उभयनिष्ठ आलेख का शीर्ष होगा -
View Solutionनिम्न व्यवरोधों `3x + 4y le 18, 2x + 3y ge 3` तथा ` x,y ge 0` सुसंगत क्षेत्र का शीर्ष हैं -
View SolutionXY- तल पर तृतीय चतुर्थांश क्षेत्र की आवश्यक दशा होगी -
View Solutionनिम्न सुसंगत क्षेत्र के लिए रेखीय व्यवरोध हैं -
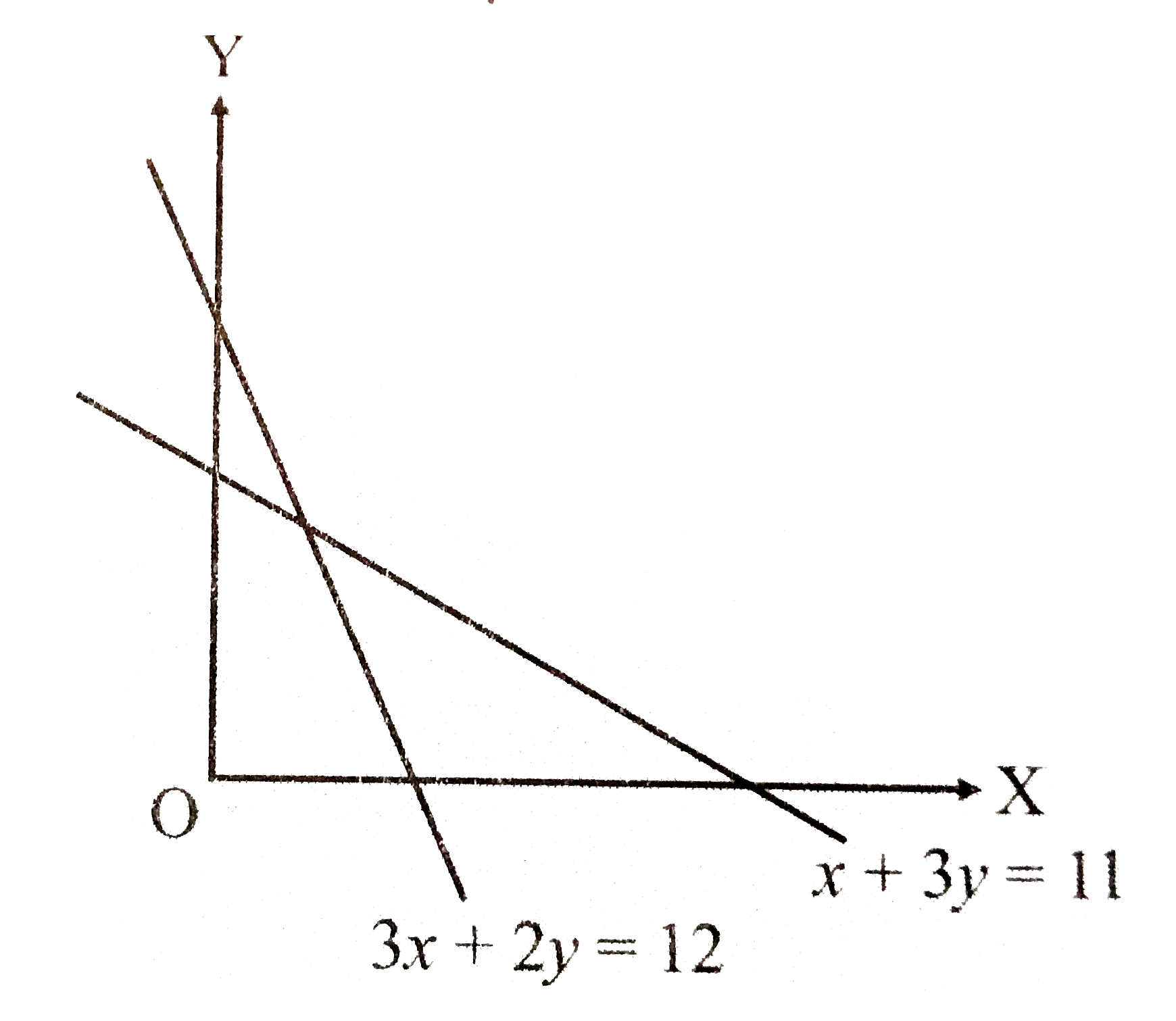
View Solution`2x+y gt 5` का हल समुच्चय हैं -
View Solution`y - x le 0` प्रदर्शित करती हैं -
View Solutionउद्देश्य फलन का न्यूनतम मान निम्न बिंदु पर प्राप्त होगा जो -
View Solutionछायांकित भाग प्रदर्शित करता है -
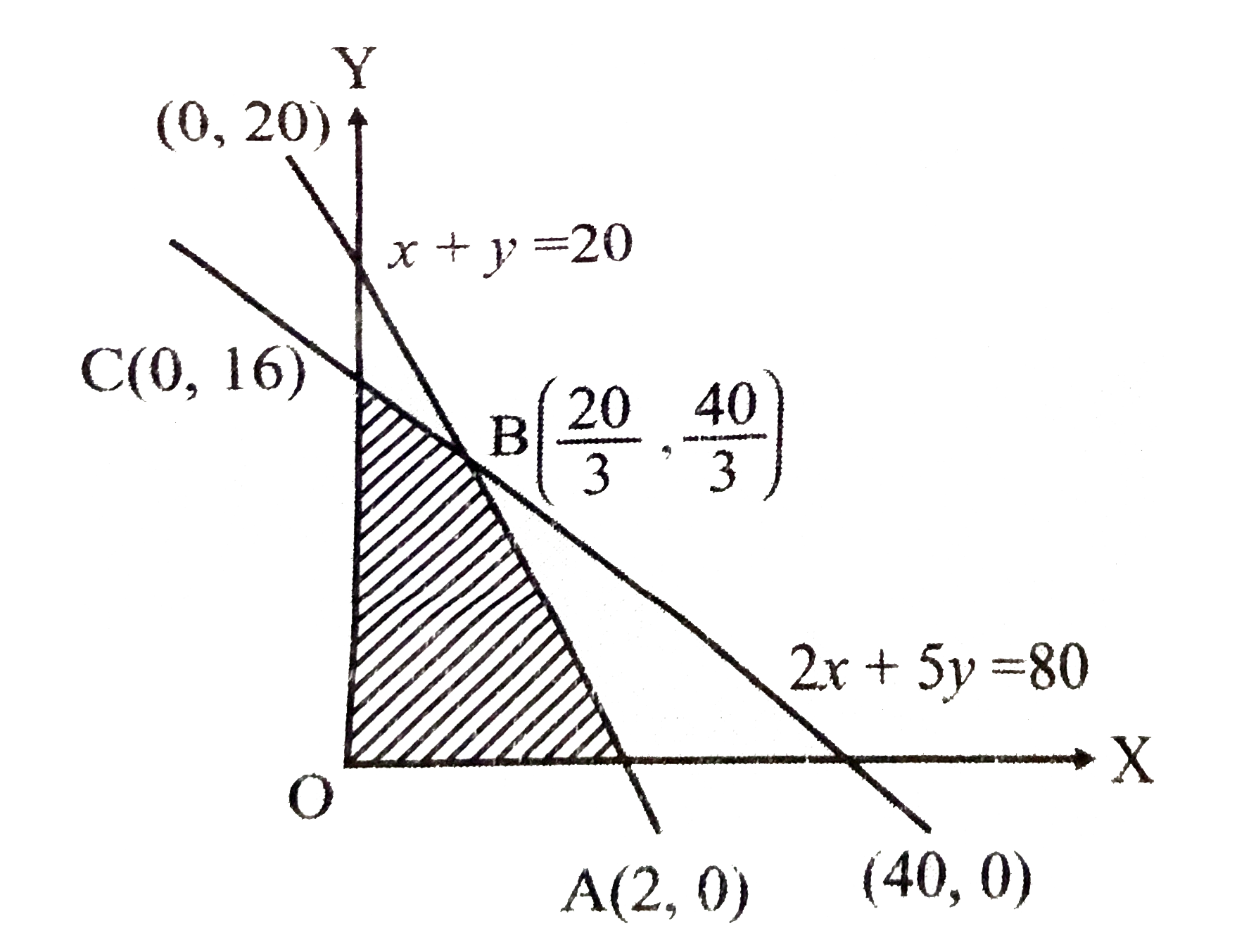
View Solutionनिम्न व्यवरोधों `3y + x ge3, xge0, yge0` के अन्तरगर्त सुसंगत क्षेत्र का क्षेत्रफल होगा -
View Solutionनिम्न व्यवरोधों के अन्तर्गत उपरोक्त चित्र में सुसंगत क्षेत्र बताओं -
`L_(1) le 0, L_(2) ge 0, L_(3) = 0 , x ge 0 , yge0`
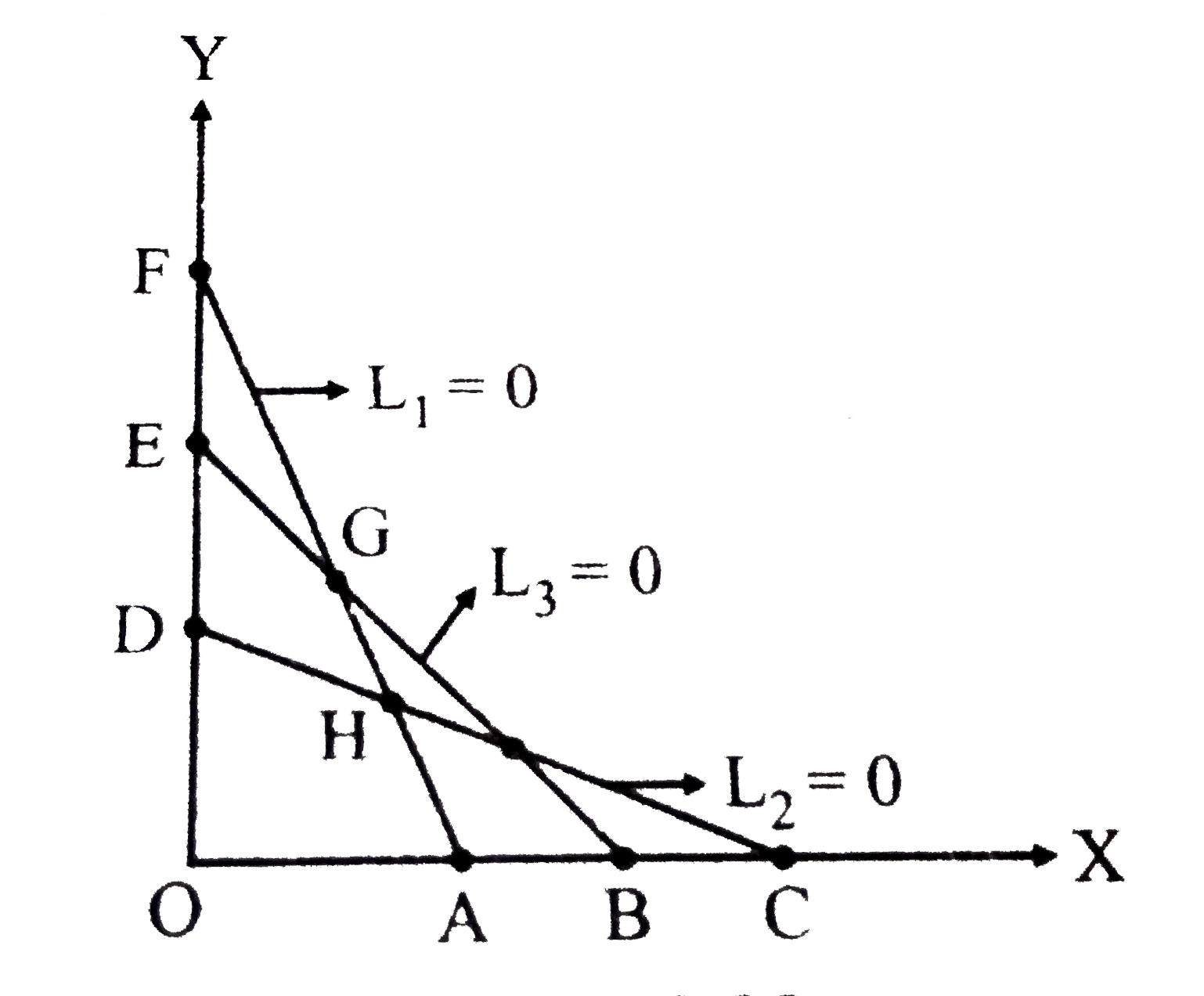
View Solutionनिम्न में से असमिका `2x + 3y le 6, 5x + 3y le 1` तथा `x,y ge 0` के द्वारा घिरा धन क्षेत्र का शीर्ष नहीं है-
View Solution
बहुविकल्पीय प्रश्न questions and complete solutions for chapter रैखिक प्रोग्रामन of SHREE BALAJI MATHS (HINDI) of Class 12