Complete Solutions to साधित उदाहरण of chapter रैखिक प्रोग्रामन of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | रैखिक प्रोग्रामन |
| BALAJI PUBLICATION | साधित उदाहरण |
| Number Of Questions | 26 |
| Academic Year | 2023-24 |
निम्न समस्या को आलेख विधि से हल करो -
अधिकतम z = `3x_(1) + 4x_(2)`
प्रतिबंध `5x_(1) + 4x_(2) le 200`
`3x_(1) + 5x_(2) le 150`
`5x_(1) + 4x_(2) ge 100`
`8x_(1) + 4x_(2) ge 80`
और `x_(1) , x_(2) ge 0`
View Solutionआलेख व्दारा निम्न रैखिक प्रोग्रामन समस्या का हल ज्ञात कीजिए
निम्न अवरोधों के अन्तर्गत
`2x + 3y le 6`
` 3x - 2y le 6`
`y le 1`
` x,yge 0`
`z = 8x + 9y` का अधिकतम मान ज्ञात कीजिए ।
View Solutionआलेख विधि से सिध्द कीजिए कि निम्न समस्या के उद्देश्य फलन का अधिकतम एंव न्यूनतम मान समान हैं -
अधिकतम ( निम्नतम) z = 5x + 3y
प्रतिबंध `x + y le 6`
`x le 3`
`y ge 3`
`2x + 3y ge 3`
तथा ` x ge 0 , y ge 0`
View Solutionनिम्न प्रोग्रामन समस्या को आलेख विधि से हल कीजिए ।
अधिकतम z `= x_(1) + 2 x_(2)`
प्रतिबंध `x_(1) le 80`
`x_(2) le 60 `
` 5x_(1) + 6 x_(2) le 600`
` x_(1) + 2x_(2) le 160`
तथा `x_(1) , x_(2) ge 0 `
View Solutionआलेखीय विधि व्दारा निम्न रैखिक प्रोग्रामन समस्या को निम्न व्यवरोधों के अंतर्गत हल कीजिए -
`2x + 4y le 8`
`3x + y le 6`
` x + y le 4`
`x ge 0 , y ge 0`
का अधिकतम मान ज्ञात कीजिए |
View Solutionएक फर्म A,B,C प्रकार के कपड़े बनाती हैं । इन कपड़ो के लिए लाल , हरी और नीली तीन प्रकार की ऊन की आवश्यकता पड़ती हैं । Aकपड़े की एक इकाई लम्बाई के लिए 2 मीटर लाल और 3 मीटर नीली ऊन , B कपड़े की एक इकाई लम्बाई के लिए 3 मीटर लाल, 2 मीटर हरी और 2 मीटर नीली ऊन तथा C कपड़े की एक इकाई लम्बाई के लिए 5 मीटर हरी , 4 मीटर नीली ऊन की आवश्यकता पड़ती हैं । फर्म के पास 16 मीटर लाल ऊन , 20 मीटर हरी और 30 मीटर नीली ऊन का स्टॉक हैं । A,B,C के लिए प्रति इकाई लम्बाई अनुमानित लाभ क्रमशः 6 रुपये , 10 रुपये और 8 रुपये हो तो बताइये कि फर्म को अपना स्टॉक किस प्रकार प्रयोग में लेना चाहिए ताकि उसे अधिकतम लाभ हो समस्या का केवल गणितीय संरुपण कीजिए ।
View Solutionएक थोक व्यापारी 24000 रुपये से अनाज का व्यापार शुरु करना चाहता हैं । गेँहू 400 रुपये प्रति क्विंटल तथा चावल 600 रुपये प्रति क्विंटल हैं । उसके स्टोर में 200 क्विंटल अनाज की क्षमता हैं । वह गेँहू पर 25 रुपये प्रति क्विटंल तथा चावल पर 40 रुपये प्रति क्विंटल लाभ कमाता हैं । यदि वह x क्विंटल चावल तथा y क्विंटल गेँहू रखता हैं तो अधिकतम लाभ के लिए इस समस्या का गणितीय रुपान्तरण कीजिए ।
View Solutionएक फर्नीचर निर्माता कुर्सी और मेज, दो प्रकार के उत्पादन करता हैं । ये दोनों उत्पादन A और B दो मशीनों पर बनती हैं । एक कुर्सी को बनाने में 2 घण्टे A मशीन पर और 6 घण्टे B मशीन पर लगते हैं । एक मेज को बनाने में 4 घण्टे A मशीन पर और 2 घण्टे B मशीन पर लगते हैं । प्रतिदिन मशीन A पर 16 घण्टे और मशीन B पर 20 घण्टे उपलब्ध हैं । निर्माता को एक कुर्सी और एक मेज से प्राप्त लाभ क्रमशः 3 रुपये तथा 5 रुपये हो तो समस्या का गणितीय संरुपण कीजिए ।
View Solutionएक कम्पनी A और B नमूने की दो चमड़े की बेल्ट बनाती हैं । बेल्ट A उच्च कोटि की एंव बेल्ट B घटिया कोटि की हैं । दोनों बेल्टों पर लाभ क्रमशः 40 तथा 30 रुपये प्रति बेल्ट हैं । A प्रकार की एक बेल्ट के बनाने में B किस्म की एक बेल्ट बनाने से दोगुना समय लगता हैं । यदि सब बेल्ट B नमूने की हों तो कम्पनी 1000 बेल्ट प्रतिदिन बना सकती हैं । लेकिन चमड़े की पूर्ति केवल 800 ( A और B दोनों को मिलाकर ) बेल्ट प्रतिदिन के लिए पर्याप्त हैं । बेल्ट A के लिए एक फेन्सी बक्कल चाहिए और उसके लिए केवल 400 बक्कल प्रतिदिन प्राप्त हैं । बेल्ट B के लिए केवल 700 बक्कल प्रतिदिन प्राप्त है । अधिकतम लाभ के लिए कम्पनी दोनों तरह की बेल्ट कितनी बनाए , आलेख विधि से हल करते हुए ज्ञात कीजिए ?
View Solutionएक आहारविद् दो भोज्यों P व Q का उपयोग करते हुए एक विशेष आहार तैयार करता हैं । भोज्य P के प्रत्येक पैकेट (जिसमें 30 ग्राम अन्तर्विष्ट हैं ) में कैल्सियम के 12 मात्रक , लौह तत्व के 4 मात्रक , कोलेस्ट्रोल के 6 मात्रक और विटामिन A के 6 मात्रक अन्तर्विष्ट है जबकि उसी मात्रा के भोज्य Q के पैकेट में कैल्सियम तत्व के 3 मात्रक , लौह तत्व के 20 मात्रक , कोलेस्ट्रोल के 4 मात्रक और विटामिन A के 3 मात्रक अन्तर्विष्ट हैं । आहार में कम से कम 240 मात्रक कैल्सियम , लौह तत्व के कम - से - कम 460 मात्रक और कोलेस्ट्रोल के अधिक - से - अधिक 300 मात्रक अपेक्षित हैं । प्रत्येक भोज्य के कितने पैकेटों का उपयोग किया जायें ताकि आहार में विटामिन A की मात्रा को न्यूनतम किया जा सकें ।
View Solutionएक फैक्ट्री दो विभिन्न उत्पादों को बनाने के लिए तीन विभिन्न साधन काम में लेती हैं । साधन A की 20 इकाई , साधन B की 12 इकाई व साधन C की 16 इकाई उपलब्ध हैं । पहले उत्पाद की एक इकाई के लिए साधनों की क्रमशः 2,2,4 इकाईयाँ की आवश्यकता पड़ती हैं । तथा दूसरे उत्पाद के लिए 4,2 और 0 इकाईयों की । यह ज्ञात है कि पहला उत्पाद 3 मुद्रा इकाई प्रति इकाई का तथा दूसरा उत्पाद 3 मुद्रा इकाई प्रति इकाई का लाभ देता हैं । रैखिक प्रोग्रामन समस्या का संरुपण कीजिए तथा लेखाचित्र विधि से बताइये कि अधिकतम लाभ के लिए प्रत्येक उत्पाद की कितनी इकाईयाँ बनायी जायें ?
View Solutionएक स्वचालित वाहन निर्माता अपनी फैक्ट्री में जो , दो कार्यशालाओं में विभाजित हैं , मोटर कारें एंव ट्रक बनाता हैं । पहली कार्यशाला में , जहाँ प्रारम्भिक ढाँचे तैयार किये जाते हैं , एक ट्रक के लिए 5 मानव दिवस तथा एक मोटर कार के लिए 2 मानव दिवस लगते हैं । दूसरी कार्यशाला में जिसमें वाहनों को अंतिम रुप दिया जाता हैं , प्रत्येक निर्मित ट्रक या मोटर कार के लिए 3 मानव दिवस लगते हैं । मशीन एंव मानव की सीमाओं के कारण पहली कार्यशाला में 180 मानव दिवस प्रति सप्ताह तथा दूसरी कार्यशाला में 135 मानव दिवस प्रति सप्ताह उपलब्ध हैं । यदि निर्माता को प्रत्येक ट्रक पर 3000 रुपये तथा प्रत्येक मोटर कार पर 2000 रुपये का लाभ हो तो लेखाचित्र विधि से ज्ञात कीजिए कि निर्मााता को अधिकतम लाभ हेतु प्रत्येक प्रकार के कितने वाहन बनाने चाहिए ?
View Solutionएक उत्पादन के कारखाने में तीन मशीनें I, II और III लगी हैं । मशीन I और II अधिकतम 12 घण्टे तक चलाए जाने की क्षमता रखती हैं । जबकि मशीन III प्रतिदिन कम - से - कम 5 घण्टे चलनी चाहिए । निर्माणकर्ता केवल दो प्रकार के सामान M और N का उत्पादन करता हैं । जिनमें प्रत्येक के उत्पादन में तीनों मशीनों की आवश्यकता होती हैं । M और N के प्रत्येक उत्पाद के एक नग उत्पादन में तीनों मशीनों के संगत लगा समय (घण्टों में ) निम्नलिखित सारणी में दिया गया हैं -

वह उत्पाद M पर 600 रुपये प्रति नग और उत्पाद N पर 400 रुपये प्रति नग की दर से लाभ कमाता हैं । मानते हुए कि उसके सभी उत्पाद बिक जाते हैं , जिनका उत्पादन किया गया हैं , तब ज्ञात कीजिए कि प्रत्येक उत्पादन के कितने नगों का उत्पादन किया जाये जिससे लाभ का अधिकतमीकरण हो अधिकतम लाभ क्या होगा ?
View Solutionएक ग्रह सज्जाकार A तथा B दो प्रकार के लैम्प बनाता हैं । दोनों लैम्प पहले एक तरासक ( cutter ) के पास तथा बाद में एक रुपाकार (finisher ) के पास जाते हैं । लैम्प A के लिए तरासक के 2 घण्टे तथा रुपाकार का एक घण्टा लगता हैं और लैम्प B के लिए तरासक का एक घण्टा तथा रुपाकार के 2 घण्टे लगते हैं । प्रत्येक माह में तरासक के पास 104 घण्टे तथा रुपाकार के पास 76 घण्टे उपलब्ध हैं । लैम्प A तथा B पर क्रमशः 6 रुपये व 11 रुपये हो तब यह मानते हुए कि निर्मित सभी लैम्प बिक जाते हैं , सज्जाकार को एक माह में अधिकतम लाभ हेतु प्रत्येक प्रकार के कितने लैम्प बनाने चाहिए ?
View SolutionP और Q दो स्थानों पर दो कारखाने स्थापित हैं । इन स्थानों से सामान A,B और C पर स्थित तीन डिपो में भेजे जाते हैं । इन डिपो की साप्ताहिक आवश्यकता क्रमशः 5,5 और 4 सामान की हैं जबकि P और Q की स्थापित कारखानों की उत्पादन क्षमता 8 और 6 नग हैं ।
प्रति नग परिवहन व्यय निम्नलिखित हैं -
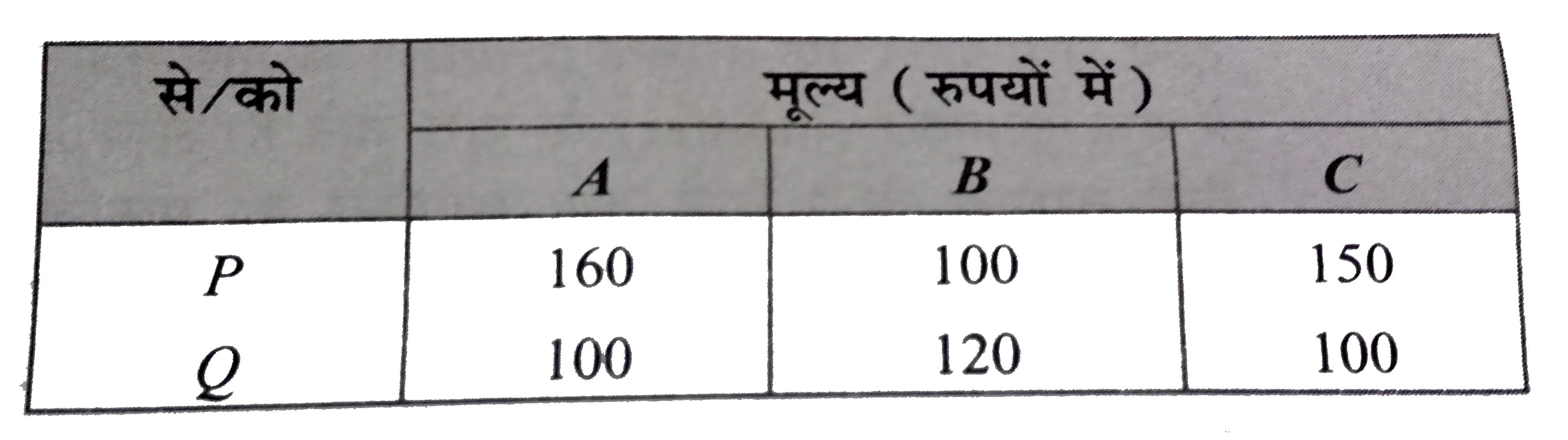
प्रत्येक कारखाने से कितने नग सामान प्रत्येक डिपो को भेजा जाए जिसमें परिवहन व्यय न्यूनतम हो ? न्यूनतम परिवहन व्यय क्या होगा ?
View Solutionआलेखीय विधि व्दारा निम्न रैखिक प्रोग्रामन समस्या को हल कीजिए , निम्न व्यवरोधों के अन्तर्गत
`x + 2y ge 10` ...(1)
` 3x + 4y ge 24` ...(2)
`x ge 0, y ge 0` ...(3)
z = 200x + 500 y का न्यूनतम मान ज्ञात कीजिए ।
View Solutionआलेखीय विधि व्दारा निम्न रैखिक प्रोग्रामन समस्या को हल कीजिए , निम्न व्यवरोधों के अन्तर्गत
` x + 3y le 60`
` x + y ge 10`
` x le y , x ge 0 , y ge 0 `
z = 3x + 9y का न्यूनतम एंव अधिकतम मान ज्ञात कीजिए ।
View Solutionदो सिलाई मास्टर A व B प्रतिदिन क्रमशः 15 रु0 व 20 रु0 कमाते हैं । A प्रतिदिन 6 कमीज और 4 पायजामा तथा B प्रतिदिन 10 कमीज व 4 पायजामा सिलता हैं । न्यूनतम लागत पर 60 कमीज और 32 पायजामा सिलने में उन्हें कितने दिन कार्य करना चाहिए ?
View Solutionएक फर्नीचर विक्रेता दो वस्तुऐं मेज तथा कुर्सी बनाता हैं । उसके पास कुल 60 वस्तुओं के लिए 5000 रुपये हैं । एक मेज का मूल्य 250 रुपये तथा कुर्सी का मूल्य 50 रुपये हैं । वह मेज को 50 रुपये के लाभ पर तथा कुर्सी को 15 रुपये के लाभ पर बेच सकता हैं । यह मानते हुए कि वह सारी वस्तुऐं बेच सकता हैं , अधिकतम लाभ कमाने के लिए अपने धन को कैसे खर्च करेगा ?
View Solutionयदि एक व्यक्ति मोटर साइकिल पर 25 किमी/घण्टा से चलता हैं । वह 2 रुपये प्रति किमी पैट्रोल पर खर्च करता हैं । यदि वह 40 किमी/घण्टा की चाल से चलता हैं तो पैट्रोल 5 रुपये प्रति किमी की दर से खर्च होता हैं । वह 100 रुपये पैट्रोल पर खर्च करें तो 1 घण्टे में तय की गयी दूरी ज्ञात करों । इसे एक रैखिक प्रोग्रामन समस्या के रुप में व्यक्त करो तथा हल करों ।
View Solutionएक कम्पनी दो प्रकार के उत्पाद A तथा B बनाती है तथा A को 5 रुपये प्रति इकाई तथा B को 3 रुपये प्रति इकाई पर बेचती हैं । प्रत्येक उत्पाद दो मशीनों `M_(1)` तथा `M_(2)` से बनता हैं । A के 1 इकाई को बनाने में 1 मिनट मशीन `M_(1)` तथा 2 मिनट मशीन `M_(2)` पर लगते हैं जबकि B के 1 इकाई को बनाने में 1 मिनट मशीन `M_(1)` तथा 1 मिनट मशीन `M_(2)` पर लगते हैं । मशीन `M_(1)` व `M_(2)` क्रमशः 5 घण्टे तथा 6 घण्टे एक दिन में काम करती हैं तो 1 दिन में अधिकतम लाभ पाने के लिए उत्पाद A तथा B की कितनी इकाइयाँ बन सकती हैं ? इसे आलेखीय विधि व्दारा हल करो ।
View Solutionएक फैक्ट्री मालिक A तथा B दो तरह की मशीने खरीदता हैं । मशीनों की आवश्यकता तथा सीमायें निम्न तालिका में गयी हैं -

उशके पास 9000 `"मीटर"^(2)` क्षेत्रफल तथा 72 कुशल श्रमिक है जो दोनों मशीनों को चला सकते हैं । वह प्रत्येक प्रकार की कितनी मशीन खरीदेगा जिससे उसे प्रतिदिन उत्पादन अधिकतम हो ?
View Solutionएक अवकाश प्राप्त व्यक्ति 70,000 रुपये निवेश कर सकता हैं तथा दो प्रकार के बॉण्ड बाजार में हैं । प्रथम बॉण्ड में निवेश की गयी धनराशि का 8 तथा दूसरे बॉण्ड में निवेश की गयी धनराशि का 10 वार्षिक मिलता हैं । उपरोक्त के अनुसार वह कम से कम 10000रुपये पहले बॉण्ड में तथा दूसरे बॉण्ड में 30,000 अधिक निवेश नहीं कर सकता हैं । एक वर्ष बाद अधिकतम रिटर्न के लिए वह किस प्रकार निवेश करेगा ?
View Solutionएक कम्पनी A , B तथा C तीन प्रकार के कैलकुलेटर I तथा फैक्ट्री II में बनाती हैं । वह कम्पनी 6400 कैलकुलेटर A प्रकार के , 4000 कैलकुलेटर B प्रकार के तथा 4800 कैलकुलेटर C प्रकार वालो का ठेका लेती हैं । फैक्ट्री I, A प्रकार के 50 कैलकुलेटर , B प्रकार के 50 कैलकुलेटर तथा C प्रकार के 30 कैलकुलेटर प्रतिदिन बनाती हैं जबकि फैक्ट्री II, A प्रकार के 40 कैलकुलेटर , B प्रकार के 20 तथा C प्रकार के 40 कैलकुलेटर बनाती हैं । फैक्ट्री I की प्रतिदिन लागत 12000 रुपये जबकि फैक्ट्री II की प्रतिदिन लागत 15000 रुपये हैं । न्यूनतम लागत पर दोनों फैक्ट्री कितने दिनों में इस ठेके को पूरा कर लेगी इसे रैखिक प्रोग्रामन समस्या के रुप में आलेखीय विधि व्दारा हल करों ।
View Solutionएक सेवानिवृत्त व्यक्ति 50000रुपये का निवेश करना चाहता हैं । उसके ब्रॉकर ने उसे दो तरह के बाण्डस A तथा B जिसमें निवेशित धन पर क्रमशः 10% और 9% रिटर्न मिलता हैं , में निवेश करने की सिफारिश की । उसने कम से कम 20000 रुपये बाण्ड A तथा कम से कम 10000 रुपये बाण्ड B में निवेश करने का निर्णय किया । वह बाण्ड A में कम से कम बाण्ड B जितना ओर निवेस करता चाहता हैं । अधिकतम रिटर्न के लिए दी गई रैखिक प्रोग्रामन समस्या को आलेखनीय विधि से हल कीजिए ।
View Solutionएक उत्पादक दो प्रकार के उत्पाद A तथा B का निर्माण करता हैं । दोनों उथ्पादों को दो विभिन्न मशीनों की आवश्यकता होती हैं । पहली मशीन की उपलब्ध क्षमता 12 घण्टे/दिन तथा दूसरी मशीन की 9 घण्टे/दिन हैं ।
उत्पाद A की प्रत्येक इकाई को दोनों मशीनों पर 3 घण्टों की आवश्यकता है तथा उत्पाद B की प्रत्येक इकाई को पहली मशीन पर 2 घण्टों तथा दूसरी मशीन पर 1 घण्टे की आवश्यकता है । उत्पाद A की प्रत्येक इकाई 7 रुपये के लाभ तथा B की 4 रुपये के लाभ पर बेची जाती हैं । आलेखनीय विधइ व्दारा अधिकतम लाभ के लिए उत्पादन स्तर प्रति दिन ज्ञात कीजिए ।
View Solution
साधित उदाहरण questions and complete solutions for chapter रैखिक प्रोग्रामन of SHREE BALAJI MATHS (HINDI) of Class 12