Complete Solutions to EXERCISE - 1 (SPECIAL DPP - 2) of chapter वृत of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | वृत |
| BANSAL HINDI | EXERCISE - 1 (SPECIAL DPP - 2) |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
यदि बिंदु `(lamda, - lamda)` वृत `x^2 + y^2 -4x+ 2y-8=0`
के अंदर स्थित हों, तो `lamda` के मानों का परिसर ज्ञात कीजिये।03:52View Solutionरेखा `4x+7y+13=0` के सापेक्ष वृत `x^2 + y^2 + 16x - 24y + 183=0` का प्रतिबम्ब होगा
07:57View Solution`y-1 = m_(1)(x-3)` तथा `y-3 = m_(2)(x-1)` दो सरल रेखा निकाय एक दूसरे के लंबवत है । उनके प्रतिच्छेदन बिंदु का बिन्दुपथ है
03:47View Solutionयदि `(a,1/a),(b,1/b),(c,1/c)`तथा `(d,1/d)`
चार भिन्न - भिन्न बिंदु 4 इकाई त्रिज्या के वृत पर स्थित है
तो abcd का मान है : (i) `4` (ii) `1/4` (iii) `1` (iv) `16`04:10View Solutionबिंदु `(x_1 , y_1),(x_2, y_2), (x_1, y_2)` तथा `(x_2, y_1)` सदैव
05:42View Solution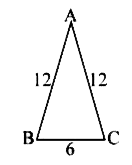
त्रिभुज ABC के शीर्षों से गुजरने वाले वृत की त्रिज्या है
(i) `(8sqrt(15))/5` (ii) `(3sqrt(15))/5` (iii) `3sqrt5` (iv) `3sqrt2`03:37View Solutionबिन्दु `A(a, 0),B(0,b),C(c, 0)` व् `D(0, d)`इस प्रकार है की ac = bd तथा a, b, c, d सभी अशून्य है तो बिन्दु
05:15View Solutionचित्र में दिखाए गए वृत का प्रथम चतुर्थेश में केंद्र के x-निर्देशांक जो रेखाओ `y=1/2x, y=4` तथा x-अक्ष को स्पर्श करता है, होगा
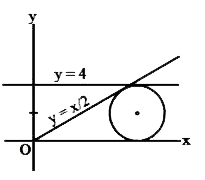 04:38View Solution
04:38View Solutionबिन्दु A(0,3) से वृत्त `x^(2)+4x+(y-3)^(2)=0` पर एक जीवा AB खींची जाती है तथा बिन्दु M तक इस प्रकार बढ़ाई जाती है , की `AM=2AB`. बिन्दु M का बिन्दुपथ ...... है।
04:45View Solutionवृत `x^2 + y^2 = 1` पर दो स्थिर बिन्दु `A(1,0)` तथा `B(0, 1)` है। C इस वृत पर एक चर बिन्दु है जैसे - जैसे C गति करता है त्रिभुज ABC के लंबकेन्द्र का बिन्दुपथ होगा
05:15View Solution
EXERCISE - 1 (SPECIAL DPP - 2) questions and complete solutions for chapter वृत of BANSAL MATHS (HINDI) of Class 12
All Exercises from BANSAL HINDI Class 12 MATHS वृत
- EXERCISE - 1 (SPECIAL DPP - 1)
- EXERCISE - 1 (SPECIAL DPP - 10)
- EXERCISE - 1 (SPECIAL DPP - 2)
- EXERCISE - 1 (SPECIAL DPP - 3)
- EXERCISE - 1 (SPECIAL DPP - 4)
- EXERCISE - 1 (SPECIAL DPP - 5)
- EXERCISE - 1 (SPECIAL DPP - 6)
- EXERCISE - 1 (SPECIAL DPP - 7)
- EXERCISE - 1 (SPECIAL DPP - 8)
- EXERCISE - 1 (SPECIAL DPP - 9)
- EXERCISE - 2
- EXERCISE - 3 (SECTION - A)
- EXERCISE - 3 (SECTION - B)
- EXERCISE - 4
- EXERCISE - 5
