Complete Solutions to EXERCISE - 5 of chapter वृत of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | वृत |
| BANSAL HINDI | EXERCISE - 5 |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
एक बिन्दु एक ऐसे वृत्त `(x+4)^2 + (y+2)^2 = 25` के अनुदिश गतिमान है जिसका केन्द्र C है। वह वृत्त से बिन्दु A या बिन्दु B पर अलग हो जाता है तथा स्पर्श रेखा के अनुदिश गति करता हुआ बिन्दु D (3.-3) से गुजरता है। निम्न को ज्ञात कीजिये।
(i) A व B पर स्पर्श रेखाओं के समीकरण
(ii) A व B के निर्देशांक
(iii) कोण ADBC व् D की वृत्त से अधिकतम व न्यूनतम दूरी
(iv) चतुर्भुज ADBC व त्रिभुज DAB का क्षेत्रफल
(v) त्रिभुज DAB के परिवृत्त का समीकरण तथा इस वृत्त के द्वारा निर्देशी अक्षों पर काटे गये अन्तः खण्डView Solutionवृत्त `x^2+y^2 =4` की उस जीवा के मध्य बिन्दु का बिन्दुपथ ज्ञात कीजिये जिसके द्वारा वक्र `x^2-2x-2y=0` पर काटा गया अन्तःखण्ड मूल बिन्दु पर समकोण अन्तरित कीजिये।
03:16View Solutionयदि रेखा y=2-x वृत्त S के बिन्दु P(1, 1) पर स्पर्श रेखा है और वृत्त S, वृत्त `x^2 +y^2+2x+2y-2 = 0` पर लम्बकोणीय हो, तो बिन्दु (2.2) से वृत्त S पर खींची गई स्पर्श रेखा की लम्बाई ज्ञात कीजिए।
07:32View Solutionएक बिन्दु A(3, 2) से वृत्त `x^2 +y^2-2x +4y-4= 0` पर स्पर्श रेखायें खींची जाती है। यदि BC स्पर्श रेखाओं की स्पर्श जीवा है, तो भुजाओं AB व् AC के मध्य बिन्दुओं को मिलाने वाली रेखा का समीकरण 4x +cy=k द्वारा दिया जाता है। (c+k) का मान ज्ञात कीजिये।
04:04View Solutionयदि चर रेखा 3x-4y+k= 0 वृत्तों `x^2 +y^2-2x-2y+1=0` तथा `x^2+y^2-16x-2y+61=0` के बीच में बिना किसी वृत्त को स्पर्श या प्रतिच्छेद करते हुये स्थित हो तथा k के मानों का परिसर (a, b) है, जहाँ a, `b in I` है, तब (b-a) का मान ज्ञात कीजिये।
07:42View Solutionमाना `S_1 = 0" व "S_2 = 0` बिन्दु P (6, 4) पर प्रतिच्छेद करने वाले दो वृत्त है तथा दोनों x अक्ष व रेखा y =mx (जहाँ `m gt 0`) को स्पर्श करते है। यदि दोनों वृत्तों `S_1 = 0 "व" S_2 = 0` की त्रिज्याओं का गुणनफल है, तो m का मान ज्ञात कीजिये।
View Solutionमाना `S:x^2+y^2-8x-6y+24=0` एक वृत्त है तथा 0 मूल बिन्दु है। माना OAB एक रेखा है जो वृत्त को A तथा B बिन्दुओं पर प्रतिच्छेद करती है। जीवा AB पर एक बिन्दु P लिया गया है। निम्न स्थितियों में P का बिन्दुपथ ज्ञात कीजियेः
(i) यदि OA तथा OB का समान्तर माध्य OP है।
(ii) यदि OA तथा OB का गुणोत्तर माध्य OP है।
(iii) यदि OA तथा OB का हरात्मक माध्य OP है।09:02View Solutionवास्तविक संख्यायें x व् y समीकरण `x^2+y^2=1` को संतुष्ट करती है। यदि व्यंजक `z=(4-y)/(7-x)` अधितम एवं न्यूनतम मान क्रमशः M व m है. तो (2M+ 6m) का मान ज्ञात कीजिये।
06:16View Solutionवृत्तों `x^2 + y^2 + 2gx + 2fy + c = 0` तथा `2x^2 + 2y^2 + 3x + 8y+2c = 0` का मूलाक्ष वृत्त `x^2+y^2+2x-2y+1=0` को स्पर्श करता है, तो प्रदर्शित करो कि या तो g=3/4 या f =2 होगा।
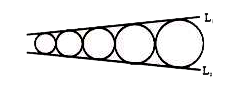
04:51View Solutionदिये गये चित्रानुसार पाँच वृत्त क्रमागत रूप से एक दूसरे को स्पर्श करते है एवं साथ ही रेखाओं `L_1` तथा `L_2` को भी स्पर्श करते है। यदि सबसे बड़े वृत्त की त्रिज्या 18 है एवं सबसे छोटे वृत्त की त्रिज्या 8 है. तो मध्य वृत्त की त्रिज्या ज्ञात कीजिये।
 02:35View Solution
02:35View Solution
EXERCISE - 5 questions and complete solutions for chapter वृत of BANSAL MATHS (HINDI) of Class 12
All Exercises from BANSAL HINDI Class 12 MATHS वृत
- EXERCISE - 1 (SPECIAL DPP - 1)
- EXERCISE - 1 (SPECIAL DPP - 10)
- EXERCISE - 1 (SPECIAL DPP - 2)
- EXERCISE - 1 (SPECIAL DPP - 3)
- EXERCISE - 1 (SPECIAL DPP - 4)
- EXERCISE - 1 (SPECIAL DPP - 5)
- EXERCISE - 1 (SPECIAL DPP - 6)
- EXERCISE - 1 (SPECIAL DPP - 7)
- EXERCISE - 1 (SPECIAL DPP - 8)
- EXERCISE - 1 (SPECIAL DPP - 9)
- EXERCISE - 2
- EXERCISE - 3 (SECTION - A)
- EXERCISE - 3 (SECTION - B)
- EXERCISE - 4
- EXERCISE - 5
