Complete Solutions to EXERCISE - 1 (SPECLAL DPP - 4 [PARABOLA]) of chapter CONIC SECTION (PARABOLA,ELLIPSE & HYPERBOLA) of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | CONIC SECTION (PARABOLA,ELLIPSE & HYPERBOLA) |
| BANSAL HINDI | EXERCISE - 1 (SPECLAL DPP - 4 [PARABOLA]) |
| Number Of Questions | 16 |
| Academic Year | 2023-24 |
एक परवलय `y^2 = 2x` के शीर्ष पर स्पर्श रेखा पर एक चर बिन्दु P से स्पर्श जीवा के लम्बवत् एक रेखा खीची जाती है। ये चर रेखाएँ सदैव एक स्थित बिन्दु से गुजरती है, जिसके निर्देशांक होगें।
04:40View Solutionरेखा `x -y+3= 0` के बिन्दुओं से परवलय `y^2 = 8x` पर स्पर्श रेखाएं खींची जाती है तब चर स्पर्श जीवा जिस स्थिर बिन्दु से जायेगी उसके निर्देशांक है
02:34View Solutionयदि परवलय `y^2 =4ax` पर दो अभिलम्ब समकोण पर काटते है तथा उनके पादों को मिलाने वाली जीवा एक स्थिर बिन्दु से गुजरती है तब स्थिर बिन्दु के निर्देशांक हैं
04:10View Solutionउस सरल रेखा का समीकरण जो बिन्दु (3,6) से गुजरती है तथा वक्र `y= sqrtx` को लम्बवत् (orthogonally) काटती है: (i) `4x + y-18=0` (ii) `x +y-9 = 0` (iii) `4x-y-6 = 0` (iv) इनमें से कोई नहीं
06:56View Solutionएक वृत्त जिसकी त्रिज्या इकाई और केन्द्र धनात्मक y - अक्ष पर है, परवलय `y = 2x^2` को P और Q पर स्पर्श करता है तब P और Q के y निर्देशांको का योग है
04:51View Solutionयदि P (2,4) पर परवलय `y^2=8x` का अभिलम्ब परवलय को पुनः Q पर मिलता है तथा PQ को व्यास मानकर खींचे गये वृत्त का केन्द्र C है तब बिन्दु C के निर्देशांक है : (i) `(10, -4)` (ii) `(-3,8)` (iii) `(10, 4)` (iv) `(-3,10)`
03:44View Solutionएक वृत्त जिसका केन्द्र C (0, 1) और त्रिज्या ईकाई है। Pएक परवलय `y=ax^2` है। तो a के उन मानों का समुच्चय जिनके लिए वे एक-दूसरे को मूल बिन्दु के अलावा एक बिन्दु पर मिलते है, होगें: (i) `a gt 0` (ii) `a in (0,(1)/2)` (iii) `(1/4,1/2)` (iv) `(1/2 , oo)`
03:26View Solutionपरवलय `y^2 = 2x` के उस जीवा के मध्य बिन्दु का बिन्दुफ्थ जो कि वृत्त `x^2+y^2- 2x-4 = 0` को स्पर्श करता है, `(y^2+1 –x)^2 = lamda(1+y^2) ` हो, तो `lamda` का मान होगा।
06:20View Solutionपरवलय `y^2=8x ` पर विचार कीजिए।
परवलय के नाभिलम्ब के चरम बिन्दुओं पर स्पर्श रेखाओं और अभिलम्बों द्वारा निर्मित आकृति का क्षेत्रफल है : (i) 8 (ii) 16 (iii) 32 (iv) 6408:08View Solutionपरवलय `y^2=8x ` पर विचार कीजिए।
परवलय की स्पर्श रेखा और समान्तर अभिलम्ब जो x अक्ष के साथ `30^@` का कोण बनाती है, के मध्य की दूरी है06:02View Solutionमाना वक्र `C:y^2-8x-4y+28 = 0` तथा वक्र C पर स्थित बिन्दु P(5,6) और Q(5,-2) पर स्पर्श रेखाएं क्रमशः TP तथा TQ है तथा P और Q पर अभिलम्ब बिन्दु R पर मिलते हैं तो
`DeltaPQR` के परिकेन्द्र के निर्देशांक होंगे (i) (5,3) (ii) (5,2) (iii) (5,4) (iv) (5,6)04:48View Solutionमाना वक्र `C:y^2-8x-4y+28 = 0` तथा वक्र C पर स्थित बिन्दु P(5,6) और Q(5,-2) पर स्पर्श रेखाएं क्रमशः TP तथा TQ है तथा P और Q पर अभिलम्ब बिन्दु R पर मिलते हैं तो
चतुर्भुज TPRQ का क्षेत्रफल होगा - (i) 8 (ii) 16 (iii) 32 (iv) 6407:24View Solutionवक्र `y^2-8x-4y+28 = 0` पर स्थित बिन्दु P(5,6) और Q(5,-2) पर खींची गयी स्पर्श रेखाओं के मध्य कोण होगा: (i) `pi/6` (ii) `pi/4` (iii) `pi/3` (iv) `pi/2`
01:59View Solutionस्तम्भ मिलान कीजिए
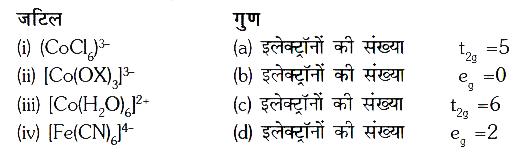 11:15View Solution
11:15View Solutionमाना `L_(1) : x +y= 0` और `L_(2): x-y= 0` उस परवलय की दो स्पर्श रेखाएं है जिसकी नाभि S(1, 2) है यदि परवलय की नाभिलम्ब की लम्बाई = `m/sqrtn` (m, n सह अभाज्य) द्वारा दर्शाते हैं तब (m + n) का मान ज्ञात कीजिए।
05:49View Solutionपरवलय `y^2 =4x` के बिन्दु P,क्यू व R पर खीची गयी अभिलम्ब यदि (15, 12) पर संगामी है, तो ज्ञात कीजिए।
(a) त्रिभुज PQR की परिवृत्त का समीकरण ज्ञात कीजिए।
(b) त्रिभुज PQR के केन्द्रक का निर्देशांक ज्ञात कीजिए।07:50View Solution
EXERCISE - 1 (SPECLAL DPP - 4 [PARABOLA]) questions and complete solutions for chapter CONIC SECTION (PARABOLA,ELLIPSE & HYPERBOLA) of BANSAL MATHS (HINDI) of Class 12
All Exercises from BANSAL HINDI Class 12 MATHS CONIC SECTION (PARABOLA,ELLIPSE & HYPERBOLA)
- EXERCISE - 1 (SPECLAL DPP - 1 [PARABOLA])
- EXERCISE - 1 (SPECLAL DPP - 2 [PARABOLA])
- EXERCISE - 1 (SPECLAL DPP - 3 [PARABOLA])
- EXERCISE - 1 (SPECLAL DPP - 4 [PARABOLA])
- EXERCISE - 1 (SPECLAL DPP - 5 [ELLTPSE])
- EXERCISE - 1 (SPECLAL DPP - 6 [ELLTPSE])
- EXERCISE - 1 (SPECLAL DPP - 7 [HYPERBOLA])
- EXERCISE - 1 (SPECLAL DPP - 8 [HYPERBOLA])
- EXERCISE - 2 (SECTION - A [PARABOLA])
- EXERCISE - 2 (SECTION - B [ELLIPSE])
- EXERCISE - 2 (SECTION - C [HYPERBOLA])
- EXERCISE - 3 (SECTION - A (JEE - ADVANCED Previous Year.s Question)) (ELLIPSE )
- EXERCISE - 3 (SECTION - A (JEE - ADVANCED Previous Year.s Question)) (HYPERBOLA)
- EXERCISE - 3 (SECTION - A (JEE - ADVANCED Previous Year.s Question)) (PARABOLA)
- EXERCISE - 3 (SECTION - B (JEE -MAIN Previous Previous Year.s Question)) (HYPERBOLA)
- EXERCISE - 4
- EXERCISE - 5
