Complete Solutions to EXERCISE - 4 (JEE ADVANCED PREVIOUS YEAR.S QUESTIONS) of chapter ROTATIONAL MECHANICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ROTATIONAL MECHANICS |
| BANSAL HINDI | EXERCISE - 4 (JEE ADVANCED PREVIOUS YEAR.S QUESTIONS) |
| Number Of Questions | 41 |
| Academic Year | 2023-24 |
M द्रव्यमान तथा R त्रिज्या का एक ठोस गोला द्रव्यमान केन्द्र से गुजर रहे अक्ष के परिता जड़त्व आघूर्ण I रखता है। इसको `t` मोटाई की एक चकती में परिवर्तित किया जाता है जिसका इसके किनारे से गुजर रहे तथा तल के लम्बवत् अक्ष के परितः जड़त्व आघूर्ण I है। तब चकती की त्रिज्या होगी।
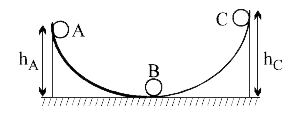
View Solutionएक गेंद चित्र में दर्शाए अनुसार एक फिक्स ट्रेक पर गति करती है। गेंद A से B तक बिना फिसले लुढ़कती है। सतह BC घर्षणहीन है। A, B तथा C पर गेंदो की गतिज ऊजाएँ क्रमशः `K_A, K_B, K_C` है। तब-
View Solutionएक ठोस बेलन `theta` आनत कोण वाले एक खुरदरे आनत तल से नीचे लुढ़क रहा है। तब-
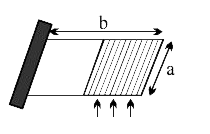
View Solution`(a xx b)` विमाओं वाली Mkg द्रव्यमान का एक आयताकार तल है। प्लेट m द्रव्यमान प्रति इकाई क्षेत्रफल प्रति एकांक समय की प्रत्येक n छोटी गेंदो की टक्कर द्वारा क्षतिज स्थिति में रखा हुआ है। प्लेट का आधा क्षेत्र (छायांकित) टक्कर में है। गेंदे प्रत्यास्थतः v वेग से टक्कर कर रही है। v क्या होगा ?
It is given `n = 100,M=3kg, m = 0.01 kg, b= 2m, a= 1m, g= 10 m//s^2`.
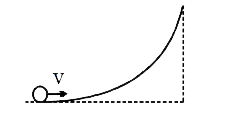
View Solutionएक समान घनत्व की एक छोटी वस्तु प्रारम्भिक वेग v से वकीय सतह के उपर लुढ़क रही है। यह प्रारम्भिक स्थिति के सापेक्ष `(3v^2)/(4g)` की अधिकतम ऊँचाई तक पहुंचती है। वस्तु है-
View Solutionदो चकतियाँ A व B एक उर्ध्वाधर अक्ष पर समअक्षीय रूप से संतुलित है। उभयनिष्ठ अक्ष के परितः इन चकतियों का जड़त्व आघूर्ण I व 2I है। `x_1` लम्बाई तक सम्पीड़ीत स्प्रिंग की स्थितिज उर्जा का उपयोग करके चकती A को प्रारम्भिक वेग `2 omega` दिया जाता है। `x_2` लम्बाई तक सम्पीड़ीत स्प्रिंग की स्थितिज उर्जा का उपयोग करके चकती B को प्रारम्भिक वेग `omega` दिया जाता है। दोनों चकतियों दक्षिणावर्त दिशा में घूम रही है।
घूर्णन `x_1//x_2`है
View Solutionदो चकतियाँ A व B एक उर्ध्वाधर अक्ष पर समअक्षीय रूप से संतुलित है। उभयनिष्ठ अक्ष के परितः इन चकतियों का जड़त्व आघूर्ण I व 2I है। `x_1` लम्बाई तक सम्पीड़ीत स्प्रिंग की स्थितिज उर्जा का उपयोग करके चकती A को प्रारम्भिक वेग `2 omega` दिया जाता है। `x_2` लम्बाई तक सम्पीड़ीत स्प्रिंग की स्थितिज उर्जा का उपयोग करके चकती B को प्रारम्भिक वेग `omega` दिया जाता है। दोनों चकतियों दक्षिणावर्त दिशा में घूम रही है।
जब चकती B को चकती A के सम्पर्क में लाया जाता है, वे 1 समय में समान कोणीय वेग प्राप्त कर लेती है। इस काल के दौरान दूसरी द्वारा पहली पर औसत घर्षण बलाघूर्ण होगा।
View Solutionउपरोक्त प्रक्रिया में गतिज ऊर्जा में व्यय होगा-
View Solutionकथन–1 : समान द्रव्यमान तथा समान विमाओं वाले दो बेलन, एक खोखला (धातु का) तथा दूसरा ठोस (लकड़ी का) को एक साथ समान ऊँचाई से एक आनत तल से बिना फिसले नीचे लुढ़कने दिया जाता है। खोखला बेलन आनत तल की तल तक पहले पहुँचता है तथा
कथन-2: ऊर्जा के संरक्षण के सिद्धान्त द्वारा दोनों बेलनो की गतिज ऊर्जाऐं समान है। जब वे आनत तल के तल तक पहुँचती है।
View Solutionआधार `10 cm xx 10 cm ` तथा ऊँचाई 15 cm का एक ब्लॉक एक आनत तल पर रखा हुआ है। इनके मध्य घर्षण गुणांक `sqrt(3)` है। क्षैतिज तल से इस आनत तल का आनत कोण `theta` धीरे-धीरे `0^@` से बढ़ता है। तब
View Solutionयदि कणों के एक निकाय पर कार्यरत सभी बाह्य बलो का परिणामी शून्य है, तब एक जड़त्व तंत्र (inertial frame) से यह कहा जा सकता है कि-
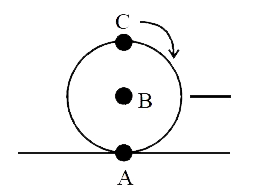
View Solutionएक गोला एक फिक्स क्षैतिज तल पर बिना फिसले लुढ़क रहा है। चित्र में A सम्पर्क बिन्दु है, गोले का केन्द्र B है तथा इसका शीर्षतम बिन्दु C है। तब
View Solution`sqrt(5)` cm व्यास के चार ठोस गोलो, प्रत्येक का द्रव्यमान 0.5 kg है, को एक 4 cm भुजा के वर्ग के कोनों पर क्रमशः रखा गया है। वर्ग के कर्ण पर इस निकाय का जड़त्व आघूर्ण यदि `N xx 10^(-4) kg-m^2`, हो, तब N का मान है-
View Solutionएक लड़का छड़ी से एक रिंग को 2N बल लगाकर धकेल रहा है, (चित्र देखिये) रिंग का द्रव्यमान 2 kg और त्रिज्या 0.5 m है। रिंग बिना फिसले `0.3 m//s^2` के त्वरण से लुढ़क रहा है। रिंग और जमीन के बीच घर्षण `(P/10)` हो, तब P का मान है।

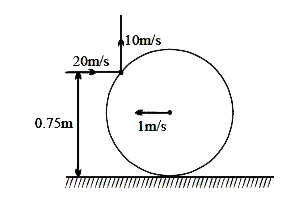
View Solution2 kg द्रव्यमान और 0.5 m त्रिज्या का एक पतला रिंग क्षैतिज तल पर बिना फिसले लुढ़क रहा है और उसका वेग 1 m/s है। 0.1 kg द्रव्यमान की एक छोटी गेंद 20 m/s के वेग, जो रिंग के वेग के विपरीत है, से चलती हुई रिंग से टकराती है। यह टक्कर जमीन से 0.75m ऊपर होती है और उसके बाद गेंद 10 m/s के वेग से सीधे ऊपर की ओर जाती है। टक्कर के तुरन्त बाद-
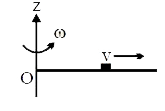
View Solutionएक पतली एकसमान छड़ बिन्दु O पर कीलकित है और क्षैतिज तल में एकसमान कोणीय चाल `omega` से घूम रही है (चित्र देखिये) | t = 0 पर एक छोटा कीड़ा O से चलना शुरू करके छड़ के अतिम सिरे पर `t =T` समय पर पहुँच कर रूक जाता है। कीड़ छड़ के सापेक्ष एकसमान चाल v से चलता है। निकाय की कोणीय चाल पूरे समय `omega` बनी रहती है। O के परितः निकाय पर लगने वाले बल-आघूर्ण का मान `|vectau|` समय के साथ जिस प्रकार बदलता है उसका सर्वोत्तम वर्णन किस ग्राफ में है ?
View Solutionएक छोटा पिंड m एक द्रव्यमान-रहित धागे से जुड़ा है। धागे का दूसरा सिरा P पर बंधित है (चित्र देखिये)। पिंड x - y तल में एकसमान कोणीय चाल `omega` से वृतीय गति कर रहा है। वृत्त का केन्द्र पर है। यदि O और P बिन्दुओं के सापेक्ष निकाले गये इस निकाय के कोणीय संवेग क्रमशः `vecL_O`और `vecL_P` हैं, तब

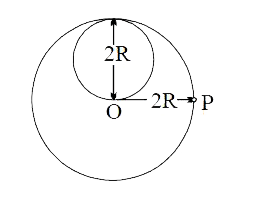
View Solutionएक एकसमान घनत्व की 2R त्रिज्या की गोल डिस्क में से एक 2R व्यास की छोटी गोल-डिस्क निकालकर एक पटल (lamina) बनाया गया है (चित्र देखिये)। इस पटल का जड़त्व-आघूर्ण O और P से जाने वाले अक्षों के परितः क्रमशः `I_0` तथा `I_P` है। दोनों अक्ष पटल के तल के लम्बवत् हैं। तब अनुपात `(I_P)/(I_0)` निकटतम पूर्णांक में क्या है ?
View Solutionव्यापक रूप में किसी दृढ़ पिंड की गति को हम दो अलग-अलग गतियों के संयुक्त रूप में देख सकते हैं: (i) उसके द्रव्यमान-केन्द्र की किसी अक्ष के परितः गति, और (ii) उसके द्रव्यमान-केन्द्र से गुजरनेवाले किसी तात्क्षणिक-अक्ष के परितः उसकी गति। यह आवश्यक नहीं है कि दोनों अक्ष स्थिर हों। उदाहरण के लिए हम दौतिज तल में रखी एकसमान डिस्क को लेते हैं जो अपनी परिधि पर एक द्रव्यमान-रहित छड़ से दृढ़ता से जुड़ी है (चित्र देखिये)। यह डिस्क-छड़ निकाय मूलबिन्दु के परितः `omega` कोणीय चाल से घर्षण-रहित क्षैतिज तल पर घूम रहा है। तब किसी भी क्षण डिस्क की गति को दो भिन्न गतियों के अध्यारोपण के रूप में देख सकते हैं। (i) डिस्क के द्रव्यमान केंद्र का z-अक्ष के सापेक्ष घूर्णन, और (ii) डिस्क का अपने द्रव्यमान-केंद्र से गुजर रहे ऊर्ध्वाधर तात्क्षणिक-अक्ष पर घूर्णन (जो कि बिंदुओं P और Q के आपस में स्थान बदलने के रूप में दिखता है)। इस उदाहरण में इन दोनों घूर्णनों की कोणीय चाल `omega` है।
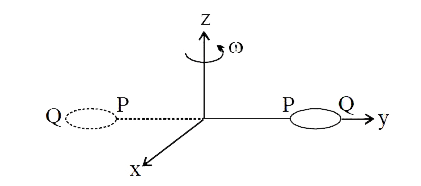
अब चित्र में दर्शाये गये उसी प्रकार के निकाय के दो भिन्न स्वरूपों (cases) पर ध्यान दें। Case (a): डिस्क का पृष्ठ ऊर्ध्वाधर है और X-Z तल के समांतर है, Case (b) : डिस्क का पृष्ठ x-y तल से `45^@` कोण बनाता है एवं उसका क्षैतिज x-अक्ष के समांतर है। दोनों cases में डिस्क बिंदु P पर जड़ित है तथा यह निकाय z-अक्ष के परितः `omega` कोणीय चाल से घूर्णन करते हैं।
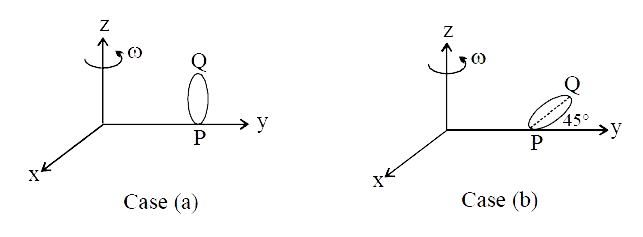
तात्क्षणिक-अक्ष (जो संहति–केंद्र से गुजर रहा है) के परितः घूर्णन की कोणीय चाल के बारे में कौन सा प्रकथन सही है?
View Solutionव्यापक रूप में किसी दृढ़ पिंड की गति को हम दो अलग-अलग गतियों के संयुक्त रूप में देख सकते हैं: (i) उसके द्रव्यमान-केन्द्र की किसी अक्ष के परितः गति, और (ii) उसके द्रव्यमान-केन्द्र से गुजरनेवाले किसी तात्क्षणिक-अक्ष के परितः उसकी गति। यह आवश्यक नहीं है कि दोनों अक्ष स्थिर हों। उदाहरण के लिए हम दौतिज तल में रखी एकसमान डिस्क को लेते हैं जो अपनी परिधि पर एक द्रव्यमान-रहित छड़ से दृढ़ता से जुड़ी है (चित्र देखिये)। यह डिस्क-छड़ निकाय मूलबिन्दु के परितः `omega` कोणीय चाल से घर्षण-रहित क्षैतिज तल पर घूम रहा है। तब किसी भी क्षण डिस्क की गति को दो भिन्न गतियों के अध्यारोपण के रूप में देख सकते हैं। (i) डिस्क के द्रव्यमान केंद्र का z-अक्ष के सापेक्ष घूर्णन, और (ii) डिस्क का अपने द्रव्यमान-केंद्र से गुजर रहे ऊर्ध्वाधर तात्क्षणिक-अक्ष पर घूर्णन (जो कि बिंदुओं P और Q के आपस में स्थान बदलने के रूप में दिखता है)। इस उदाहरण में इन दोनों घूर्णनों की कोणीय चाल `omega` है।
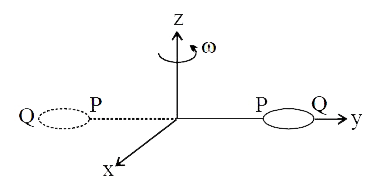
अब चित्र में दर्शाये गये उसी प्रकार के निकाय के दो भिन्न स्वरूपों (cases) पर ध्यान दें। Case (a): डिस्क का पृष्ठ ऊर्ध्वाधर है और X-Z तल के समांतर है, Case (b) : डिस्क का पृष्ठ x-y तल से `45^@` कोण बनाता है एवं उसका क्षैतिज x-अक्ष के समांतर है। दोनों cases में डिस्क बिंदु P पर जड़ित है तथा यह निकाय z-अक्ष के परितः `omega` कोणीय चाल से घूर्णन करते हैं।
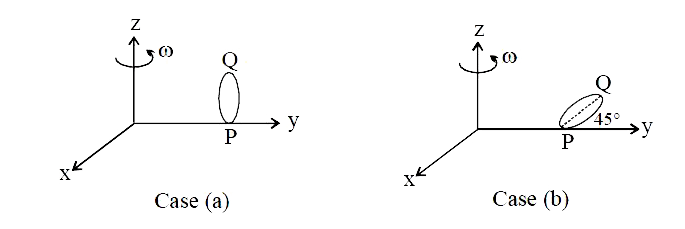
तात्क्षणिक-अक्ष (जो द्रव्यमान केंद्र से गुजर रहा है) के बारे में कौन सा प्रकथन सही है?
View Solutionचित्र में दिखाये निकाय के हिस्से हैं : (i) 3R बाहरी–त्रिज्या की वलय, जो क्षैतिज सतह पर `omega` कोणीय चाल से दक्षिणावर्त बिना फिसले लुढ़क रही है, और (ii) 2R त्रिज्या की भीतरी चकती जो `omega//2` कोणीय चाल से वामावर्त घूम रही है। घर्षण-रहित बॉल-बियरिंग (गोलियाँ) वलय और डिस्क को एक दूसरे से अलग रखते हैं। निकाय x-z तल में है। भीतरी डिस्क पर बिंदु P मूल बिन्दु से R दूरी पर है और OP क्षैतिज से `30^@` का कोण बनाता है। तब क्षैतिज सतह के सापेक्ष
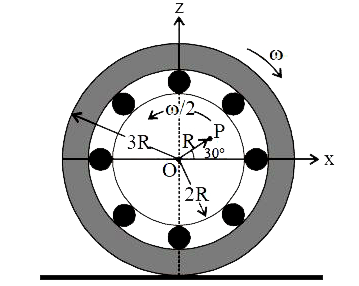
View Solutionसमान द्रव्यमान और समान त्रिज्या के दो ठोस बेलन Pऔर Q एक जड़ आनत तल पर समान ऊँचाई से एक ही समय लुढ़कना शुरू करते हैं। बेलन P का अधिकतर द्रव्यमान उसकी सतह की ओर केंद्रित है और बेलन Q का अधिकतर द्रव्यमान उसके अक्ष की ओर केंद्रित है। तब कौन प्रकथन सही है/हैं?
View Solution50 kg व 0.4m त्रिज्या की एक एक समान चकती अपनी ऊर्ध्वाधर अक्ष के सापेक्ष `10 rad s^(-1)` के कोणीय वेग से घूम रही है। दो एकसमान वृत्ताकार वलय धीरे से चकती पर एक दूसरे को छूते हुए इस प्रकार चकती तल पर रखे जाते हैं कि वे चकती के अक्ष को भी स्पर्श करें। प्रत्येक वलय का द्रव्यमान 6.25 kg व त्रिज्या 0.2 m है। इस निकाय का नया कोणीय वेग (`rad s^(-1)` में) निम्न होगा (मान लीजिये कि चकती एवम् वलय के बीच घर्षण इतना है कि चकती व वलय के बीच सापेक्ष गति शून्य है और निकाय मूल अक्ष पर घूर्णन कर रहा है):
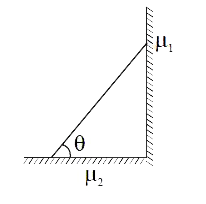
View Solutionद्रव्यमान m वाली एक सीढ़ी दीवार के सहारे तिरछी खड़ी है, जैसा चित्र में दर्शाया गया है। क्षैतिज फर्श से `theta` कोण बनाते हुए यह स्थैतिक साम्यावस्था में है। दीवार व सीढ़ी के बीच घर्षण गुणाक `mu_1` है तथा फर्श व सीढ़ी के बीच घर्षण गुणाक `mu_2` है। दीवार द्वारा सीढ़ी पर लगाया गया अभिलम्बित प्रतिक्रिया बल `N_1` तथा फर्श द्वारा सीढ़ी पर लगाया गया अभिलम्बित प्रतिक्रिया बल `N_2` है। जब सीढ़ी सरकने वाली हो, तब
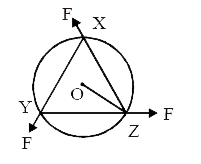
View Solutionएक एकसमान वृत्ताकर डिस्क जिसका द्रव्यमान 1.5 kg तथा त्रिज्या 0.5 m है, प्रारम्भ में घर्षण रहित क्षैतिज सतह पर विरामावस्था में है। बराबर परिमाण F= 0.5N वाले तीन बल एक साथ t=0 पर चित्र में दिखाये गये समबाहु त्रिभुज XYZ, जिसके शीर्ष विन्दु डिस्क की परिधि पर स्थित है, की भुजाओं के अनुदिश लगाए जाते हैं। बलों को लगाने के 1 सेकण्ड पश्चात् डिस्क Y की कोणीय गति, `rad s^(-1)` में है :
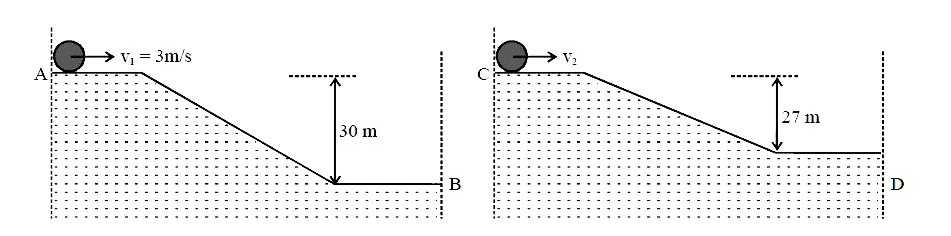
View Solutionचित्रानुसार दो भिन्न सतहों AB व CD पर समान वृत्ताकार चक्रिकाएं (डिस्क) A तथा C से क्रमशः `v_1` तथा `v_2` प्रारंभिक रेखीय वेगों से बिना फिसलते हुए लुढ़कना शुरू करती है तथा सदैव सतहों के संपर्क में रहती हैं। यदि B तथा D बिंदुओं पर पहुँचकर दोनों चक्रिकाओं के रेखीय वेग बराबर हैं तथा `v_1 = 3 m//s` है, तब `m//s` में `v_2` का मान है `(g = 10 m//s^2)`
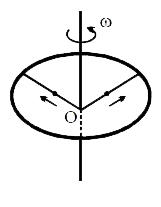
View Solutionएक द्रव्यमान M तथा त्रिज्या R का छल्ला अपने केन्द्र O से होकर जाने वाली स्थिर ऊर्ध्वाधर अक्ष के चारों ओर `omega` कोणीय गति से घूम रहा है। इस समय पर `M/8` द्रव्यमान के दो बिंदु द्रव्यमान छल्ले के केन्द्र O पर विराम में हैं। वो दर्शाय चित्रानुसार छत्ले पर लगी द्रव्यमान रहित दो छड़ों पर त्रिज्यतः बाहर की ओर गति कर सकते हैं। किसी एक क्षण पर निकाय की कोणीय गति `8/9omega` है तथा एक बिंदु द्रव्यमान O से `3/5R` की दूरी पर है। इस क्षण दुसरे बिंदु द्रव्यमान की O से दूरी होगी
View Solution1.6 kg द्रव्यमान और l लम्बाई की एकसमान लकड़ी की एक डंडी एक चिकनी खड़ी दीवार, जिसकी ऊँचाई `h (< l)` है, पर आनत तरीके से इस तरह से रखी गयी है कि डंडी का एक छोटा सा भाग दीवार से ऊपर निकला हुआ है। डंडी पर दीवार का प्रतिक्रिया बल डंडी के लम्बरूप में है। डंडी दीवार के साथ `30^@` का कोण बना रही है और डंडी का आधार एक घर्षण वाली जमीन पर है। दीवार से डंडी पर प्रतिक्रिया तथा जमीन से डंडी पर प्रतिक्रिया की मात्रा समान है। `h//l` का अनुपात एवं डंडी के आधार पर घर्षण बल f है `(g= 10 ms^(-2))`
View Solutionm द्रव्यमान के एक कण का स्थिति-सदिश | नीचे समीकरण में दिया गया है
`vecr (t) = alpha t^3 hati + beta t^2 hatj`
जिसमें `alpha = 10//3 ms^(-3),beta = 5 ms^(-2)` एवं `m = 0.1 kg ` हैं। समय `t=1s` पर, निम्नलिखित में से कौनसा/ कौनसे कथन सत्य है/हैं?
View Solutionm तथा 4m द्रव्यमान वाली दो पतली वृत्ताकार चत्रिकाएँ (discs), जिनकी त्रिज्याऐं क्रमशः a तथा 2a हैं, के केन्द्रों को `l = sqrt(24)a` लम्बाई की द्रव्यमान-रहित द्रढ़ (rigid) डंडी से जोड़ा गया है। इस समूह को एक मजबूत समतल सतह पर लिटाया गया है और फिसलाये बिना इस तरह से घुमाया गया है कि इसकी कोणीय गति डंडी के अक्ष के गिर्द `omega` है । पूरे समूह का बिन्दु `'omega'` के गिर्द कोणीय संवेग `vecL` है (चित्र देखिये) । निम्नलिखित में से कौनसा/कौनसे कथन सत्य है /हैं ?
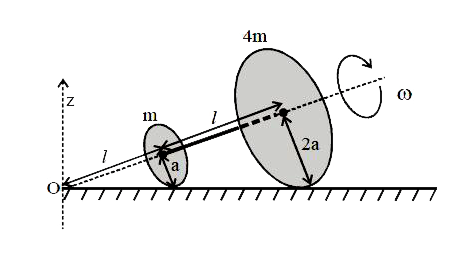
View Solutionएक निर्देश तंत्र जो एक जड़त्वीय निर्देश तंत्र की तुलना में त्वरित हो, अजड़त्वीय निर्देश तंत्र कहलाता है। स्थिर कोणीय वेग `omega` से घूमती हुई डिस्क पर बद्ध (fixed) निर्देश तंत्र अजड़त्वीय तंत्र का एक उदाहरण है। m द्रव्यमान का एक कण घूमती हुई डिस्क पर गतिमान है। गतिमान कण डिस्क पर बद्ध निर्देश तंत्र के सापेक्ष बल `vecF_("rot")` तथा एक जड़त्वीय निर्देश तंत्र के सापेक्ष बल `vecF_m` को महसूस करता है। `vecF_("rot")` और `vecF_m` में के बीच का सम्बन्ध निम्नलिखित समीकरण में दिया गया है
`vecF_("rot") = vecF_m + 2m (vecV_("rot") xx vecomega) + m(vecomega xx vecr) xx vecomega`
यहाँ पर `vecV_("rot")` घूमते हुए निर्देश तंत्र में कण का वेग है तथा `vecr` कण का डिस्क के मध्य बिन्दु के सापेक्ष स्थिति सदिश (position vector) है। माना कि R त्रिज्या की एक डिस्क, जिसमें व्यास के समानान्तर एक घर्षणरहित खाँचा है, एक स्थिर कोणीय गति `omega` से अपने अक्ष पर वामावर्त दिशा में घूम रही है। एक निर्देश तंत्र मानिए जिसका मूलबिन्दु डिस्क के मध्य बिन्दु पर है एवं x-अक्ष खाँचे के समानान्तर है, y-अक्ष खाँचे के अभिलम्ब पर है एवं z-अक्ष घूमने वाली अक्ष के समानान्तर है `(vecomega = omega hatk)`| m द्रव्यमान वाले एक छोटे गुटके को समय `t = 0` पर `vecr = (R//2)hati` बिन्दु पर धीरे से इस तरह से रखा जाता है कि वो सिर्फ खाँचे में ही चल सके।
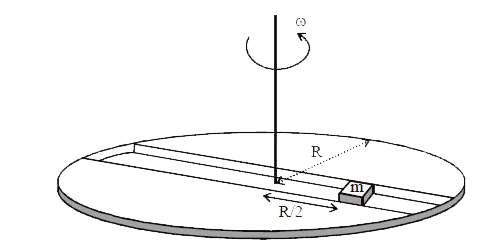
समय t पर गुटके की दूरी r का मान है :
View Solutionएक निर्देश तंत्र जो एक जड़त्वीय निर्देश तंत्र की तुलना में त्वरित हो, अजड़त्वीय निर्देश तंत्र कहलाता है। स्थिर कोणीय वेग `omega` से घूमती हुई डिस्क पर बद्ध (fixed) निर्देश तंत्र अजड़त्वीय तंत्र का एक उदाहरण है। m द्रव्यमान का एक कण घूमती हुई डिस्क पर गतिमान है। गतिमान कण डिस्क पर बद्ध निर्देश तंत्र के सापेक्ष बल `vecF_("rot")` तथा एक जड़त्वीय निर्देश तंत्र के सापेक्ष बल `vecF_m` को महसूस करता है। `vecF_("rot")` और `vecF_m` में के बीच का सम्बन्ध निम्नलिखित समीकरण में दिया गया है
`vecF_("rot") = vecF_m + 2m (vecV_("rot") xx vecomega) + m(vecomega xx vecr) xx vecomega`
यहाँ पर `vecV_("rot")` घूमते हुए निर्देश तंत्र में कण का वेग है तथा `vecr` कण का डिस्क के मध्य बिन्दु के सापेक्ष स्थिति सदिश (position vector) है। माना कि R त्रिज्या की एक डिस्क, जिसमें व्यास के समानान्तर एक घर्षणरहित खाँचा है, एक स्थिर कोणीय गति `omega` से अपने अक्ष पर वामावर्त दिशा में घूम रही है। एक निर्देश तंत्र मानिए जिसका मूलबिन्दु डिस्क के मध्य बिन्दु पर है एवं x-अक्ष खाँचे के समानान्तर है, y-अक्ष खाँचे के अभिलम्ब पर है एवं z-अक्ष घूमने वाली अक्ष के समानान्तर है `(vecomega = omega hatk)`| m द्रव्यमान वाले एक छोटे गुटके को समय `t = 0` पर `vecr = (R//2)hati` बिन्दु पर धीरे से इस तरह से रखा जाता है कि वो सिर्फ खाँचे में ही चल सके।
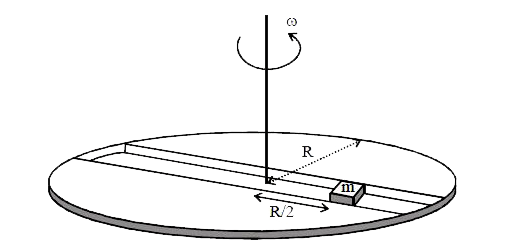
गुटके पर डिस्क की नेट प्रतिक्रिया (net reaction) है :
View Solutionचित्र द्वारा दर्शाये समबहुभुजों की भुजाओं की संख्या n=3, 4, 5......... है। सभी बहुभुजों का संहति केन्द्र (center of mass) अनुभूमिक तल से hऊँचाई पर है। ये बिना फिसले क्षितिज तल पर प्रतिगामी शीर्ष (leading vertex) के चारों ओर घूर्णन कर अग्रसरित हो रहे है। प्रत्येक बहुभुज के संहति केन्द्र के रेखापथ (locus) की ऊँचाई की अधिकतम वृद्धि `Dleta` हैं तब `Delta` की h और n पर निर्भरता निम्न में से दी जाएगी।

View Solutionएक Lलम्बाई का द्रढ़ दंड (rigid bar)ABअपनी ऊर्ध्वाधर स्थिति से घर्षणहीन तल (frictionless horizontal surface) पर चित्रानुसार फिसल रहा है। समय के किसी क्षण पर दंड द्वारा उर्ध्वाधर से बनाया कोण 0 है। निम्न में से कौनसा(से) प्रकथन सही है/हैं?

View Solutionएक त्रिज्या R एवं द्रव्यमान M का पहिया (wheel) एक Rऊँचाई वाले दृढ़ सोपान (step) के तल पर रखा है। (जैसे चित्र में दिखाया गया है) पहिये को सोपान पर चढ़ाने मात्र के लिये एक अचर बल पहिये के पृष्ठ पर सतत (continuous constant force) कार्यरत है। कागज के पृष्ठ से अभिलंब दिशा में (perpendicular to the plane of the paper) बिन्दु Q से जाने वाली अक्ष के सापेक्ष बलआघूर्ण `tau` मानिये। निम्न में से कौन (सा) से प्रकथन सही है/हैं?
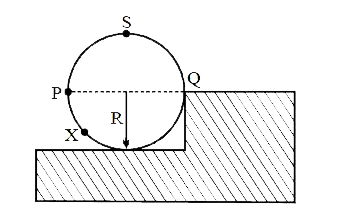
View Solutionएक वृत्ताकार वलय (द्रव्यमान M एवं त्रिज्या R) एक उंगली के परितः धुतघूर्णन करता है (जैसा चित्र 1 में दर्शाया गया है)। इस प्रक्रम में उंगली वलय के आंतरिक पृष्ठ से हमेशा स्पर्श करती है। उंगली एक शंकु के पृष्ठ का अनुरेखिय पथ का अनुसरण करती है जैसे की बिन्दुकित रेखा द्वारा दर्शाया गया है। उंगली एवं वलय के स्पर्श बिन्दु के अनुरेखिय पथ की त्रिज्या । है। उंगली कोणीय वेग `omega_(0)` से घूर्णन कर रही है। वलय । त्रिज्या वाले वृत्त के बाहरी पृष्ठ पर फिसलन रहित घूर्णन करता है। जैसा चित्र 2 में वलय एवं उंगली के स्पर्श बिन्दु द्वारा दर्शाया गया है। वलय एवं उंगली के बीच घर्षण गुणांक `mu` एवं गुरूत्वीय त्वरण g है
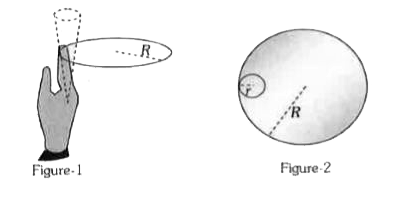
न्यूनतम `omega _(0 )` जिसके कम होते ही वलय गिर जायेगा वह है
View Solutionएक वृत्ताकार वलय (circular ring)(द्रव्यमान M एवं त्रिज्या R) एक उंगली के परित ध्रुतघूर्णन करता है (जैसा चित्र 1 (figure 1) में दर्शाया गया है) इस प्रक्रम में उंगली वलय के अंतरिक पृष्ठ से हमेशा स्पर्श करती है। उंगली एक शंकु (cone) के पृष्ठ का अनुरेखिय पथ का अनुसरण करती है जैसे कि बिन्दुकित रेखा द्वारा दर्शाया गया है। उंगली एवं वलय के स्पर्श विन्दु के अनुरेखिय पथ की त्रिज्या r है। उंगली कोणीय वेग `omega_0` से घूर्णन कर रही है। वलय r त्रिज्यावाले वृत्त के बाहरी पृष्ठ पर फिसलन रहित घूर्णन (rolls without slipping) करता है। जैसा चित्र 2 (figure2) में वलय एवं उंगली के स्पर्श बिंदु द्वारा दर्शाया गया है। वलय एवं उंगली के बीच घर्षण गुणांक (coefficient of friction) `mu` एवं गुरूत्वीय त्वरण g है।
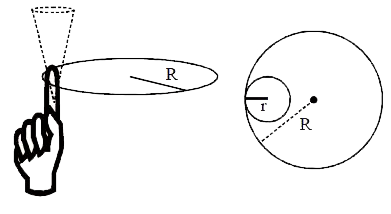
वलय की कुल गतिज ऊर्जा है
View Solutionद्रव्यमान (mass)m के एक कण की स्थितिज ऊर्जा (potential energy) `V(r) = kr^2//2` है, जहाँ r एक नियत बिन्दु (fixed point)O से कण दूरी है और k उचित विमाओं (dimensions) वाला एक धनात्मक नियतांक (positive constant) है। यह कण बिन्दु O के सापेक्ष R त्रिज्या वाली एक वृत्तीय कक्षा (circular orbit) में घूम रहा है। यदि v कण की चाल है और L बिन्दु O के सापेक्ष इसके कोणीय संवेग (angular momentum) का परिमाण (magnitude) है, तो निम्नलिखित कथनों में से कौनसा(से) सही है (है)?
View Solution1.0 kg द्रव्यमान (mass) की एक वस्तु समय t = 0 पर मूलबिन्दु (origin) पर विरामावस्था में है। इस वस्तु पर उएक बल `vecF = (alpha hati + beta hatj)` लगाया जाता है, जहाँ `alpha = 1.0 Ns^(-1)`और `beta = 1.0 N` हैं। समय `t = 1.0s` पर मूलबिंदु के सापेक्ष वस्तु पर लगने वाला बल आघूर्ण (torque) `vectau` है। निम्नलिखित कथनों में से कौनसा (से) सही है (है)?
View Solutionएक वृत्ताकार वलय (ring) और एक वृत्ताकार चकती (disc), एक आनत तल (inclined plane) के शीर्ष पर अलग-बगल (side by side) विरामावस्था में हैं। आनत तल, क्षैतिज तल (horizontal plane) से `60^@` का कोण बनाता है। दोनों वस्तुएं एक ही पल, न्यूनतम दूरी वाले पथ पर बिना फिसले लौटना (rolling without slipping) आरम्भ करती हैं। यदि दोनों वस्तुओं क्षैतिज तल पर पहुँचने का समयांतर `(2 - sqrt(3))//sqrt(10)s`, हो तो आनत तल के शीर्ष की ऊँचाई……... मीटर है। `g-10 ms^(-2)` लें।
View Solutionनीचे दी गयी सूची-I में, एक कण के चार विभिन्न पथ, समय के विभिन्न फलनों (function) के रूप में दिये गये हैं। इन फलनों में `alpha` और `beta`उचित विमाओं वाले धनात्मक नियतांक (positive constants) हैं, जहाँ `alpha != beta` प्रत्येक पथ में कण पर लगने वाला बल या तो शून्य है या संरक्षी (conservative) है। सूची-II में कण की पाँच भौतिक राशियों का विवरण दिया गया है : `vecp` रेखीय संवेग (linear momentum) है, `vecL` मूल बिन्दु (origin) के सापेक्ष कोणीय संवेग (angular momentum) है,Kगतिज ऊर्जा (kinetic energy) है, U स्थितिज ऊर्जा (potential energy) है और E कुल ऊर्जा (total energy) है। सूची-I के प्रत्येक पथ का सूची-II में दिये गये उन राशियों में सुमेल कीजिये, जो उस पथ के लिए संरक्षी (conserved) है।
`{:("कॉलम I","कॉलम II"),(P. vecr(t) = alpha t hati + beta t hatj, 1. vecp),(Q. vecr(t) = alpha cos omega t hati + beta sin omega t hatj, 2. vecL),(R. vecr(t) = alpha(cos omega hati + sin omegat hatj),3. K),(S. vecr(t) = alphat+ beta/2 t^2 hatj,4. U),(,5. E):}`
View Solution
EXERCISE - 4 (JEE ADVANCED PREVIOUS YEAR.S QUESTIONS) questions and complete solutions for chapter ROTATIONAL MECHANICS of BANSAL PHYSICS (HINDI) of Class 12
All Exercises from BANSAL HINDI Class 12 PHYSICS ROTATIONAL MECHANICS
- EXERCISE - 1 (OBJECTIVE QUESTIONS)(MATRIX TYPE)
- EXERCISE - 1 (OBJECTIVE QUESTIONS)(MULTIPLE CORRECT CHOICE TYPE)
- EXERCISE - 1 (OBJECTIVE QUESTIONS)(PARAGRAPH TYPE)
- EXERCISE - 1 (OBJECTIVE QUESTIONS)(REASONING TYPE)
- EXERCISE - 1 (OBJECTIVE QUESTIONS)(SINGLE CORRECT CHOICE TYPE)
- EXERCISE - 2 (SUBJECTIVE QUESTIONS)
- EXERCISE - 3 (JEE MAIN PREVIOUS YEAR.S QUESTIONS)
- EXERCISE - 4 (JEE ADVANCED PREVIOUS YEAR.S QUESTIONS)
- EXERCISE - 5 (POTENTIAL PROBLEMS BASED ON CBSE)
- ILLUSTRATION