Complete Solutions to PHYSICS PART (A) of chapter TEST PAPERS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | TEST PAPERS |
| BANSAL | PHYSICS PART (A) |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
The reation between the time t and position x for a particle moving on x-axis is given by `t=px^(2)+qx`, where p and q are constants. The relation between velocity v and acceleration a is as
05:56View SolutionA particle moves from A to B in a circular path of radius R covering an angle `theta` as shown in figure. Find the ratio of magnitude of distance and magnitude of displacement of the particle.
 02:02View Solution
02:02View SolutionFind the minimum force required so that the resultant should come in the direction of `+ve` X-axis only.
View SolutionThere are two vectors Force `vec(A) = (hat(i) + 3 hat(j) - hat(k)) N` and Position `vec(B) = (hat(i) + 3 hat(j) - hat(k))m` that can be used by two students Alia and Varun. Following are the steps following by each of them.
Alia : Step 1 : Calculate unit vector of `vec(A)` by dividing it by its magnitude and get
`hat(A) = (hat(i) + 3 hat(j) - hat(k))/(sqrt11)`
Alia : Step 2 : Get a displacement vector of magnitude `10m` using `hat(A)`
Displacement vector `= (10(hat(i) +3 hat(j) - hat(k))/(sqrt11)) m`
Varun : Step 1 : Calculate unit vector of `vec(B)` by dividing `vec(B)` by its magnitude and get,
`hat(B) = ((hat(i) + 3 hat(j) - hat(k))/(sqrt11))`
Varun : Step 2 : Get a force vector of magnitude `10 N` by using `vec(B)`
Force vector `= (10(hat(i) + 3 hat(j) - hat(k)) N)/(sqrt11)`
Siddharth, a third student, comes and says when we divide or multiply a vector by a scalar, then the physical quantity represented by the vector from a displacement vector from a force vector or a force vector from a displacement vector as calculated by Alia and Varun repectivley.
Who is/are correct ?02:20View SolutionIn a new system of units 1 unit mass is `4 kg`, 1 unit length is 3 meters and 1 unit time is 2 seconds. Now find x such that 1unit force in new system becomes x newton.
03:02View SolutionIf C ( the velocity of light ) g , ( the acceleration due to gravity), P ( the atmospheric pressure) are the fundamental quantities in MKS system , then the dimensions of length will be same as that of
02:10View SolutionAn automobile can accelerate or decelerated at a maximum value of `5m//s^(2)` and can attain a maximum speed of `90 km`hr. It it starts from rest. What is the shortest time in which can travel 80 metre. If it is comes to rest at the end of the 80 metre run ?
07:40View SolutionA particle moves along x-axis. At time `t = 0`, the particle is at origin and its initial veclocity is along positive x-direction. The plot of its `("speed")^(2)` versus its x-coordinate is as shown in graph.

As the particle moves the acceleration of particle :02:51View SolutionA particle moves along x-axis. At time `t = 0`, the particle is at origin and its initial veclocity is along positive x-direction. The plot of its `("speed")^(2)` versus its x-coordinate is as shown in graph.

The time at which velocity of particle is zero.03:17View SolutionA particle moves along x-axis. At time `t = 0`, the particle is at origin and its initial veclocity is along positive x-direction. The plot of its `("speed")^(2)` versus its x-coordinate is as shown in graph.
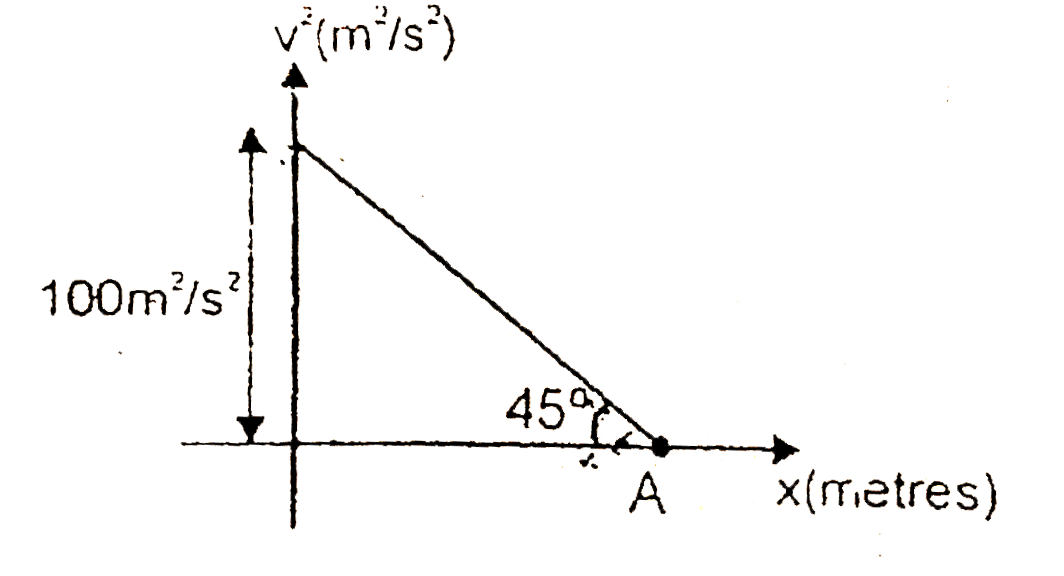
The velocity time graph for th eparticle upto point A is best represented by (assuming velocity as positive in positive x-direction):04:22View SolutionIn the equation `x = A sin omegat + Be^(alpha^(2))`, x is length and t its time. Find correct option for the dimensional formula of A, B, C and `omega`.
View SolutionWhich of th efollowing is/are correct regarding vectors `vec(A) = 2hat(i) + hat(j)` and `vec(B) = 2hat(i) - 4 hat(j)`.
07:08View SolutionA particle has initial velocity `12 m//s`. It moves due to a constant force along the line of velocity which initially produces retardation of `8 m//s^(2)`. Then :
03:55View SolutionThe displacement (x) of particle depends on time (t) as
`x = alpha t^(2) - beta t^(3)`.04:48View SolutionThe trajectory of a projectile is given by `y=x tantheta-(1)/(2)(gx^(2))/(u^(2)cos^(2)theta)`. This equation can be used for calculating various phenomena such as finding the minimum velocity required to make a stone reach a certain point maximum range for a given projection velocity and the angle of projection required for maximum range. The range of a particle thrown from a tower is define as the distance the root of the tower and the point of landing.
In the previous problem, what should be the corresponding projection angle.03:22View SolutionThe trajectory of a projectile is given by `y=x tantheta-(1)/(2)(gx^(2))/(u^(2)cos^(2)theta)`. This equation can be used for calculating various phenomena such as finding the minimum velocity required to make a stone reach a certain point maximum range for a given projection velocity and the angle of projection required for maximum range. The range of a particle thrown from a tower is define as the distance the root of the tower and the point of landing.
In the previous problem, what should be the corresponding projection angle.03:22View SolutionA student tries to raise a chain consisting of three identical links. Each link has a mass of `300 gm`. The three piece chain is connected to a string and suspended vertically, while the student holding the upper end of he string, pulling it upward. Beacause of the student's pull an upwards force of `12 N` is applied to the chain by the string. `(g = 10 m//s^(2))`
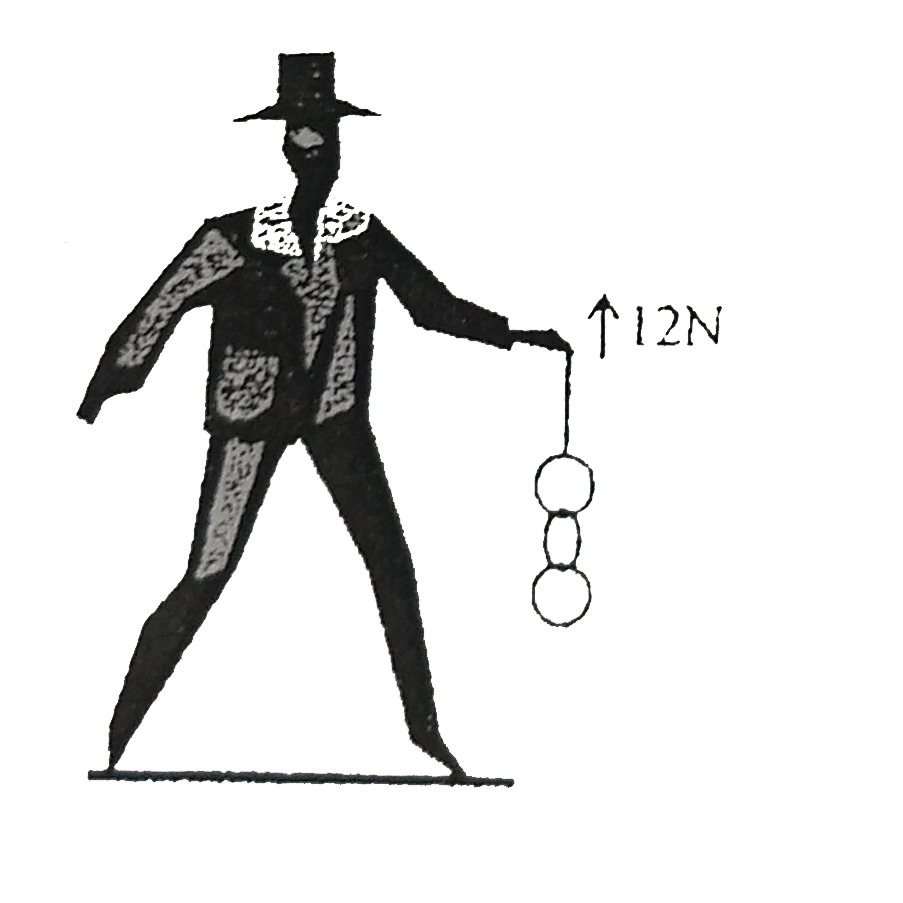
Acceleration of chain is07:35View SolutionA student tries to raise a chain consisting of three identical links. Each link has a mass of `300 gm`. The three piece chain is connected to a string and suspended vertically, while the student holding the upper end of he string, pulling it upward. Beacause of the student's pull an upwards force of `12 N` is applied to the chain by the string. `(g = 10 m//s^(2))`
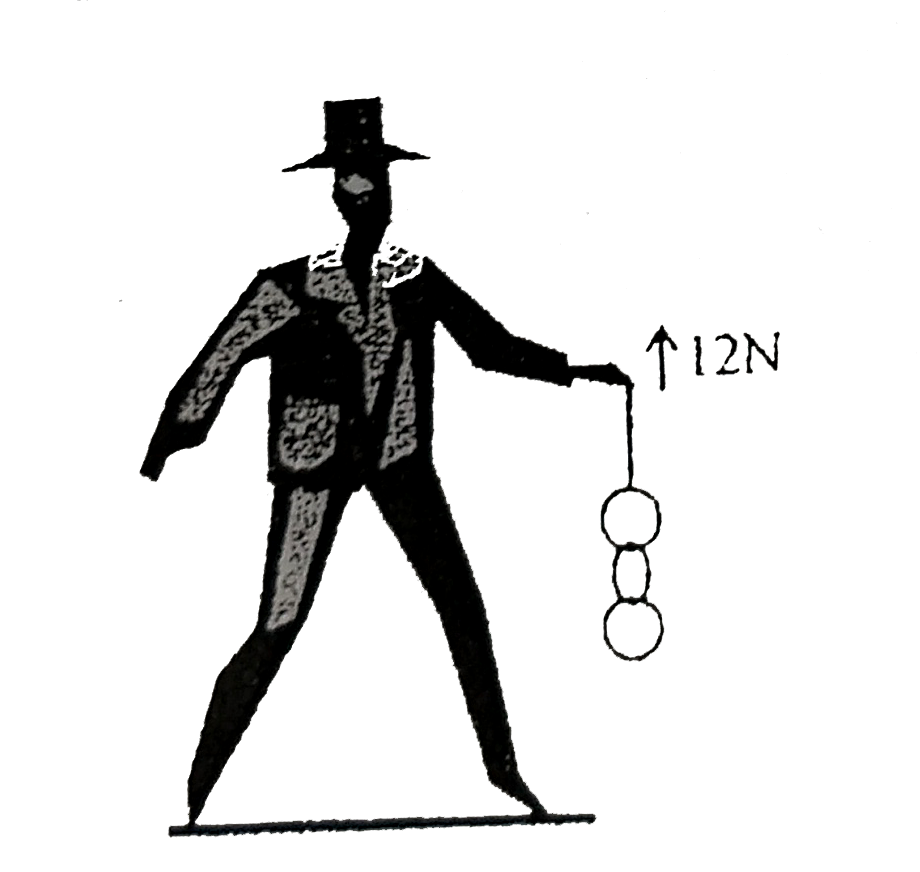
The force exerted by the top link on the middle link.07:35View SolutionA boat B is moving in upstream with velocity `3 m//s` with respect to ground. An observer standing on boat obsserves that a swimmer S is crossing the river perpendicular to the direction of motion of boat. If river flow velocity is `4 m//s` and swinner crosses the river of width `100m` in 50 sec, then
06:15View SolutionThe displacement x of a particle varies with time according to the relation `x=(a)/(b)(1-e^(-bt))`. Then select the false alternative.
04:42View SolutionThe figure shows a smooth fixed wedge on which a block of mass m is kept and released, then which of the following (s) are true.
(`vec(a) =` acceleration of block and N is the contact force between the block and the wedge)
 06:27View Solution
06:27View Solutionif `vec(P) xx vec(R ) = vec(Q) xx vec(R )`, then
03:10View SolutionA boy in a open trucj throws a ball at `40 m//s` at angle `60^(@)` form horizontal. The truck is moving with constant speed `10 m//s` and the boy just after throw, jumps off the truck and starts running in same direction to catch the ball. (Assume same horizontal level)
 05:49View Solution
05:49View SolutionIf a particle is moving along a straight line and following is the graph showing acceleration varying with time then choose the correct statement (s) for interval t = 0 to t = 8 sec, At t = 0, x = 0 and `v_(0) = 7 m//s`
View SolutionIn the arrangement shown, the pulleys are massless and frictionless. The rope connected to the block is also light and inexlensible. The system is in equilibrium. Select the correct alternative.
 04:21View Solution
04:21View SolutionA block can slides down an inclined plane of slope and `theta`, with constant velocity. If it is projected up the same plane with an initial speed `v_(0)`, then
09:54View SolutionA particle is projected in air with an initial velocity u directed at an angle `theta` above horizontal. After time `t_(0)` the velocity of the particle is directed at angle `phi` above horizontal.
07:40View SolutionA particle of mass m suspended by a string of length l revolves in a horizontal circle such that `theta` is the angle which the string makes with vertical. Which of the following statement (s) is/are correct ?
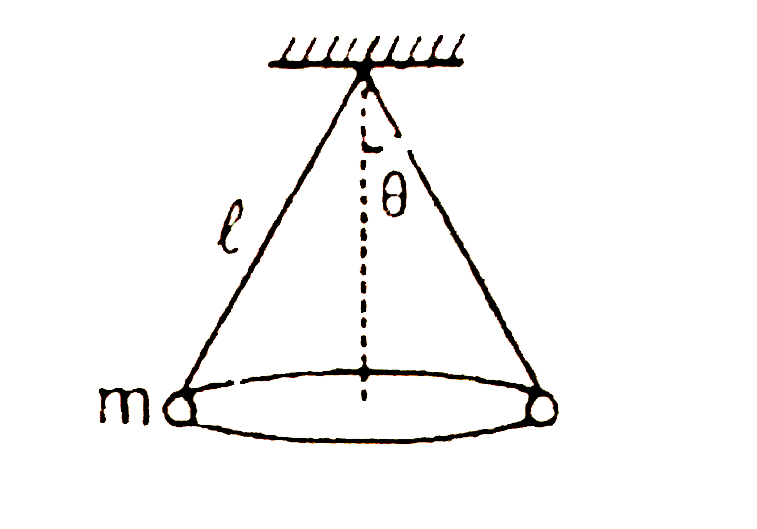 04:07View Solution
04:07View SolutionA block B starts sliding down from the point A on a rough wedge. The angle that the incline plane makes with the horizontal is variable having value `(pi)/(3)` at A and 0 at B. Also the magnitude of rate of change of `theta` with x is 2 where x is the length measured along the incline plane starting from A. Assume total length of incline plane to be `(pi)/(6)m`. Based upon the above situation, answer the following question. `(x ge (pi)/(24)m)`
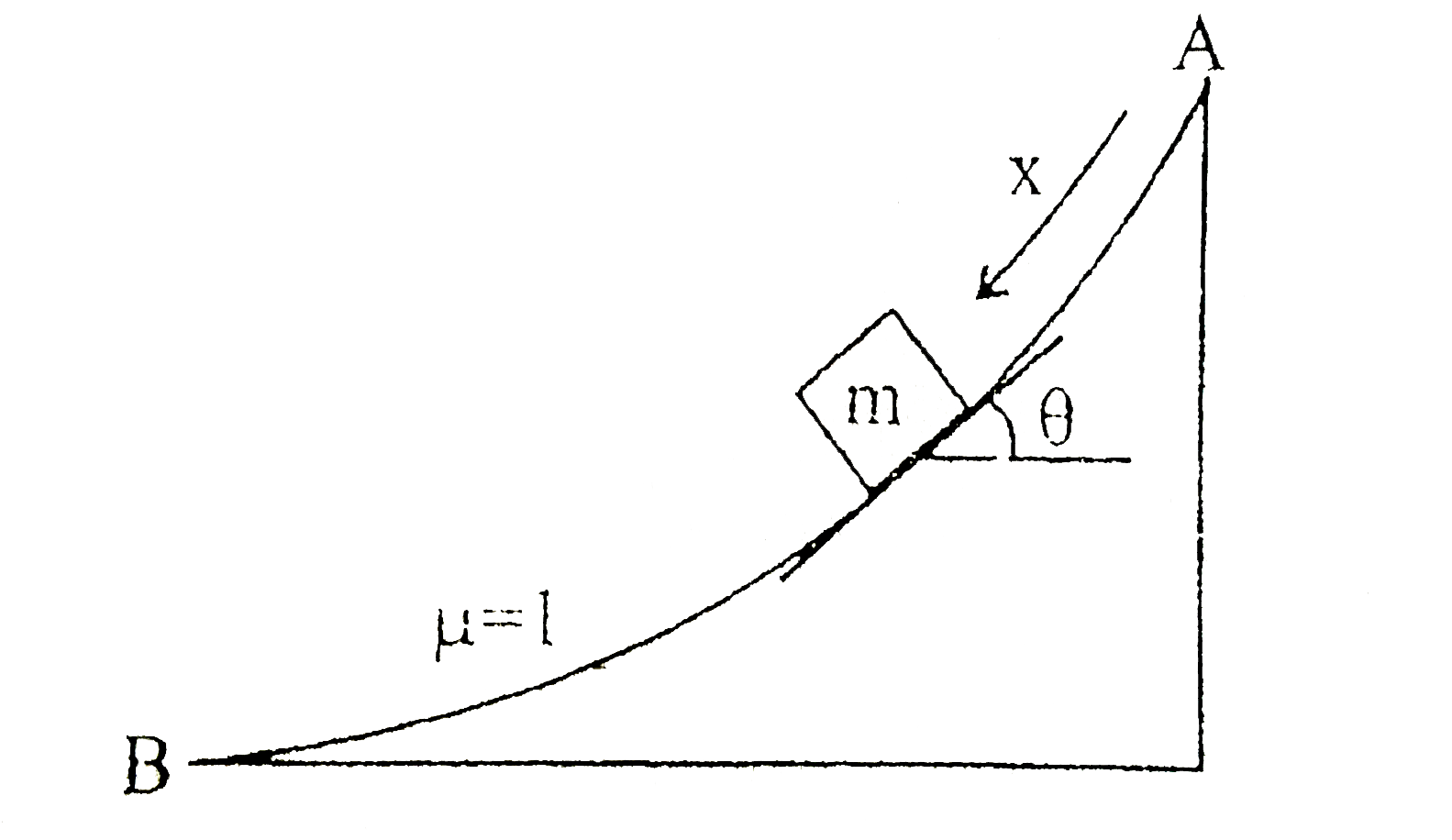
Find x in metre such that the block is in equilibrium over ther08:22View SolutionA block B starts sliding down from the point A on a rough wedge. The angle that the incline plane makes with the horizontal is variable having value `(pi)/(3)` at A and 0 at B. Also the magnitude of rate of change of `theta` with x is 2 where x is the length measured along the incline plane starting from A. Assume total length of incline plane to be `(pi)/(6)m`. Based upon the above situation, answer the following question. `(x ge (pi)/(24)m)`
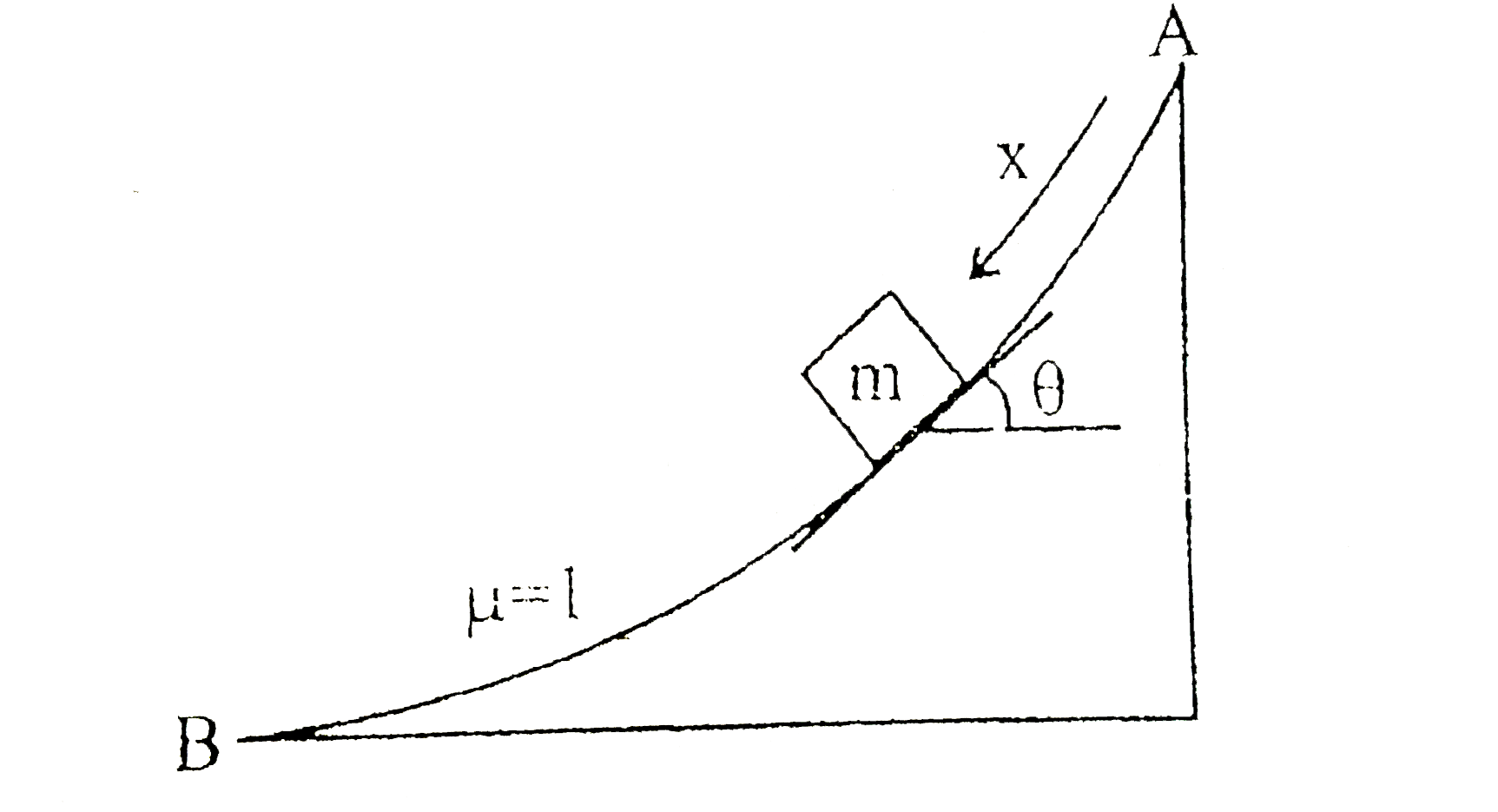
Find velocity of the block as it reaches down at the point B.08:57View SolutionA particle starts moving at t = 0 in a circle of radius `R = 2m` with constant angular acceleration of `a - 3 "rad/sec"^(2)`. Initial angular speed of the particle is 1 rad/sec. At time `t_(0)` the angle between the acceleration vector and the velocity vector of the particle is `37^(@)`.
What is the value of `t_(0)` ?07:59View SolutionA particle starts moving at t = 0 in a circle of radius `R = 2m` with constant angular acceleration of `a - 3 "rad/sec"^(2)`. Initial angular speed of the particle is 1 rad/sec. At time `t_(0)` the angle between the acceleration vector and the velocity vector of the particle is `37^(@)`.
What is the magnitude of the acceleration of the particle at `t_(0)` ?06:59View Solution
PHYSICS PART (A) questions and complete solutions for chapter TEST PAPERS of BANSAL PHYSICS (HINGLISH) of Class 12
