Complete Solutions to EXERCISE of chapter APPLICATION OF INTEGRALS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | APPLICATION OF INTEGRALS |
| BODY BOOKS PUBLICATION | EXERCISE |
| Number Of Questions | 53 |
| Academic Year | 2023-24 |
Find the points of intersection of the parabola `y^2=8x` and the line y=2x.
View SolutionThe area bounded by the parabola `y^(2)=8x` and its latus rectum (in sq unit) is a)`16//3` b)`32//3` c)`8//3` d)`64//3`
View SolutionFind the area enclosed between the curve
`x^2=4y`
and the line x = 4y - 2
View SolutionDraw the graph of the function `y=x^2` and `x=y^2` in a coordinate axis.
View SolutionConsider the parabolas `y^2=4x`,`x^2=4y`
Find the point of intersection of the
two parabolas.
View SolutionGiven the graphs of `y=x^2` and `x=y^2`. Express the area of the region bounded by the parabolas as a definite integral.
View SolutionConsider the parabolas `y=x^2` and `y^2=x`.
Find the area of the region bounded by the two parabolas.
View SolutionFind the area of the region bounded by the curve `y^2=8x` and the x-axis at x=1 and x=3.
View SolutionDraw the rough sketch of `y^2+1=x`,`xle2` and find the area enclosed by the curve and the ordinate at x=2.
View SolutionUsing integration find the area of the region bounded by the curves `y=x^2+2`, y=x,x=0 and x=3.
View SolutionDraw a rough sketch of the region enclosed by `y^2=x` and x+y=2.
View SolutionDraw a rough sketch of the curves y=x and `y=x^3`.
View SolutionDraw a rough sketch of the curves y=sinx and y=cosx as 'x' varies from 0 to `pi//2`.
View SolutionFind the points of intersection of the parabola `y^2=8x` and the line y=2x.
View SolutionFind the area of the region bounded by the curve `y=|x|` and the x-axis between x=-4 and x=2.
View SolutionFind the area bounded by the curve `y=cos x` between `x=0` and `x=2 pi`
View SolutionChoose the correct answer. Smaller area enclosed by the circle `x^2+y^2 =4` and the line x+y=2 is:
View SolutionFind the area of a circle of radius r, by integration.
View SolutionFind the area of the circle ,
`x^2+y^2=16`
which Is exterior to parabola
`y^2=6x`
View SolutionThe area of the triangular region whose sides are y = 2x +1, y = 3x + 1 and x = 4 is a)5 b)6 c)7 d)8
View SolutionChoose the correct answer. Area of the region bounded by the curve`y^2=4x`, y-axis and the line y=3 is :
View SolutionThe area between `x=y^2` and `x=4 is divided into two equal parts by the line x=a, find the value of a.
View SolutionSketch the graph of `y=|x+3|`and evaluate `overset0underset(-6)int|x+3|`dx.
View SolutionFind the area lying above x-axis and included between the circle `x^2+y^2=8x` and parabola `y^2=4x`.
View SolutionFind the area of the region bounded by the `y^2=4ax` and `x^2=4ay`, a>0
View SolutionUsing integration find the area of the region bounded by the parabola `y^2=4x`and the circle `4x^2+4y^2=9`.
View SolutionDraw the graph of the function `y=x^2` and `x=y^2` in a coordinate axis.
View SolutionConsider the functions f(x)=sinx and g(x)=cosx in the interval `[0,2pi]` Find the x coordinates of the meeting points of the functions.
View SolutionConsider the functions` f(x) = sin x `and `g(x) = cos x `in the interval
`[0,2 pi]`
draw the rough sketch of the above function ?
View SolutionConsider the functions` f(x) = sin x` and `g(x) = cos x` in the interval
`[0,2 pi]`
find the area enclosed by these curves in the given interval ?
View SolutionShade the area enclosed by `x^2=4y,y=2,y=4` and the y-axis in the first quadrant ?
View SolutionFind the area of the circle ,
`x^2+y^2=16`
which Is exterior to parabola
`y^2=6x`
View SolutionDraw a rough sketch of the graph of the function
`y^2=4x`
View SolutionMake a rough sketch of the curves `y=x^2` and y=|x|.
View SolutionThe co-ordinates of the vertices of `triangleABC` are A(2,0), B(4,5) and C(6,3).Find the equations of the sides AB,BC and CA.
View SolutionThe co-ordinates of the vertices of `triangleABC` are A(2,0), B(4,5) and C(6,3).Find the equations of the sides AB,BC and CA.
View SolutionThe area bounded by the curve y=f(x), x-axis and the line x=a and x=b is ?
View SolutionArea bounded by the curve `y=f(x)`,x axis and the linesx=a and `x=b` is
View SolutionFind the area bounded by the curve y= sin x with x-axis, between x=0 and `x=2 pi`
View SolutionFind the area of the region bounded by the curve
`y^2=x`
x-axis and the lines x=1 and x=4
View SolutionArea bounded by the curves y=cosx ,`x=pi/2`, x=0, y=0 is
View SolutionFind the area of the region bounded by the `y^2=4ax` and `x^2=4ay`, a>0
View SolutionThe area bounded by the curve above the x-axis, between `x = a` and `x = b` is
View SolutionFind the area of the circle
`x^2+y^2=4`
using integration
View SolutionConsider the function
`f(x)=abs(x)+1,g(x)=1-abs(x)`
sketch the graph and shade the enclosed region between them
View SolutionConsider the functions: `f(x)=|x|-1` and `g(x)=1-|x|`. Find the area of their shaded region.
View SolutionFind the point at which the circle `x^2+y^2=32` intersects the positive x-axis.
View SolutionShade the region in the first quadrant enclosed by x-axis, the line y=x and the circle `x^2+y^2=32`
View SolutionFind the area bounded by the curve y= sin x with x-axis, between x=0 and `x=2 pi`
View SolutionFind the area of the region bounded by the ellipse `x^2/4 + y^2/9 =1`.
View SolutionChoose the correct answer. Area lying between the curves `y^2=4x` and y=2x is :
View SolutionFind the area between the curves y=x and `y=x^2`.
View SolutionChoose the correct answer. Area bounded by the curve`y=x^3`,The x-axis and the ordinates.
x=-2 and x=1 is: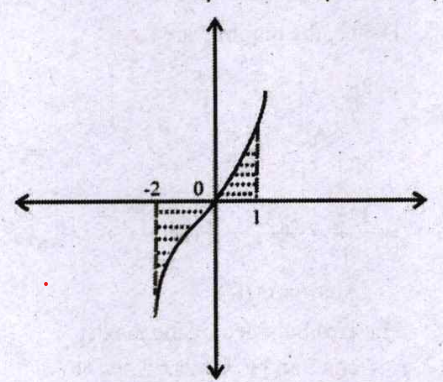
View Solution
EXERCISE questions and complete solutions for chapter APPLICATION OF INTEGRALS of BODY BOOKS PUBLICATION of Class 12