Complete Solutions to All Questions of chapter APPLICATION OF INTEGRALS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | APPLICATION OF INTEGRALS |
| Mathematics | All Questions |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Find the area of the figure enclosed by the curve `5x^2+6x y+2y^2+7x+6y+6=0.`
View SolutionIf the area by `y=x^2+2x-3` and the line `y=k x+1` is the least, find `k` and also the least area.
View SolutionArea enclosed by the curve `y=f(x)` defined parametrically as `x=(1-t^2)/(1+t^2), y=(2t)/(1+t^2)` is equal
View SolutionSketch and find the area bounded by the curve `sqrt(|x|)+sqrt(|y|)=sqrt(a)` and `x^2+y^2=a^2` (where `a > 0). If curve `|x|+|y|=a` divides the area in two parts, then find their ratio in the first quadrant only.
View SolutionLet `f(x)=min (x+1,sqrt(1-x))` for all `xlt=1.` Then the area bounded by `y=f(x)` and the x-axis is (a) `7/3` sq units (b) `1/6` sq units (c) `(11)/6` sq units (d) `7/6` sq units
View SolutionThe area enclosed by `2|x|+3|y|lt=6` is 3 sq. units (b) 4 sq. units 12 sq. units (d) 24 sq. units
View SolutionIf `A_n` is the area bounded by `y=x` and `y=x^n ,n in \mathbb{N}` ,then `A_2 A_3 ... A_n=` (a) `1/(n(n+1))` (b) `1/(2^n n(n+1))` (c) `1/(2^(n-1)n(n+1))` (d) `1/(2^(n-2)n(n+1))`
View SolutionArea enclosed between the curves `|y|=1-x^2` and `x^2+y^2=1` is (a) `(3pi-8)/3` (b) `(pi-8)/3` (c) `(2pi-8)/3` (d) None of these
View SolutionIf the area of bounded between the x-axis and the graph of `y=6x-3x^2` between the ordinates `x=1` and `x=a` is `19` units, then `a` can take the value: (A) 4 or -2 (B) one value is in (2, 3) and one in (-1, 0) (C) one value is in (3, 4) and one in (-2,-1) (D) none of these
View SolutionThe area enclosed between the curves `y=(log)_e(x+e),x=(log)_e(1/y),` and the x-axis is (a) `2s qdotu n i t s` (b) `1s qdotu n i t s` (c) `4s qdotu n i t s` (d) none of these
View SolutionIf `A_n` be the area bounded by the curve `y=(tanx)^n` and the lines `x=0,\ y=0,\ x=pi//4` , then for `n > 2.`
View SolutionFind all the possible values of `b >0,` so that the area of the bounded region enclosed between the parabolas `y=x-b x^2a n dy=(x^2)/b` is maximum.
View SolutionIn the hexaploid wheat, the haploid (n) and basic (x) numbers of chromosomes are
View SolutionLet `O(0,0),A(2,0),a n dB(1 1/(sqrt(3)))` be the vertices of a triangle. Let `R` be the region consisting of all those points `P` inside ` O A B` which satisfy `d(P , O A)lt=min[d(p ,O B),d(P ,A B)]` , where `d` denotes the distance from the point to the corresponding line. Sketch the region `R` and find its area.
View SolutionA copper rod of mass m rests on two horizontal rails distance L apart and carries a current of I from one rail to the other. The coefficient of static friction between rod and rails is `mu_(s)` What are the (a) magnitude and (b) angle (relative to the vertical) of the smallest magnetic field that puts the rod on the verge of sliding?
View SolutionThe area bounded by the x-axis, the curve `y=f(x),` and the lines `x=1,x=b` is equal to `sqrt(b^2+1)-sqrt(2)` for all `b >1,` then `f(x)` is
View SolutionA particle moves along x-axis such that its position veries with time as `x=50t-5t^2`. Select the correct alternative (s).
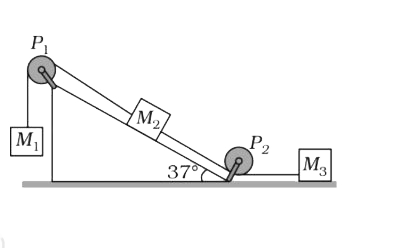
View SolutionMasses `M_(1), M_(2)` and `M_(3)` are connected by strings of negligible mass which pass over massless and frictionless pulleys `P_(1)` and `P_(2)` as shown in the figure. The masses move such that the portion of the string between`P_(1)` and `P_(2)` is parallel to the inclined plane and the portion of the string between `P_(2)` and `M_(3)` is horizontal. The masses `M_(2)` and `M_(3)` are 4.0 kg each and the coefficient of kinetic friction between both the masses and the surfaces is 0.25. The inclined plane makes an angle of 37° with the horizontal. If the mass `M_(1)` moves downwards with a uniform velocity, find
(i) the mass of `M_(1)` in kg
(ii) the tension in the horizontal portion of the string in Newton
View SolutionThe area bounded by the two branches of curve `(y-x)^2=x^3` and the straight line `x=1` is (a) `1/5s qdotu n i t s` (b) `3/5s qdotu n i t s` `4/5s qdotu n i t s` (d) `8/4s qdotu n i t s`
View SolutionThe area bounded by the curves `y=log_e x ` and `y=(log_e x)^2` is (A) `e-2` sq. units (B) `3-e` sq. units (C) `e` sq. units (D) `e-1` sq. units
View SolutionThe area of the region containing the points `(x , y)` satisfying `4lt=x^2+y^2lt=2(|x|+|y|)` is (a)`8s qdotu n i t s` (b) `2s qdotu n i t s` (c)`4pis qdotu n i t s` (d) `2pis qdotu n i t s`
View SolutionLet `f(x)=x^3+3x+2a n dg(x)` be the inverse of it. Then the area bounded by `g(x)` , the x-axis, and the ordinate at `x=-2a n dx=6` is (a) `9/4s qdotu n i t s` (b) `4/3s qdotu n i t s` (c) `5/4s qdotu n i t s` (d) `7/3s qdotu n i t s`
View SolutionConsider two curves `C_1: y^2=4[sqrt(y)]x a n dC_2: x^2=4[sqrt(x)]y ,` where [.] denotes the greatest integer function. Then the area of region enclosed by these two curves within the square formed by the lines `x=1,y=1,x=4,y=4` is (a)`8/3s qdotu n i t s` (b) `(10)/3s qdotu n i t s` (c)`(11)/3s qdotu n i t s` (d) `(11)/4s qdotu n i t s`
View SolutionThe area enclosed between the curve `y^2(2a-x)=x^3` and the line `x=2a` above the x-axis is (a) `pia^2s qdotu n i t s` (b) `(3pia^2)/2s qdotu n i t s` (c) `2pia^2s qdotu n i t s` (d) `3pia^2s qdotu n i t s`
View SolutionThe area of the region of the plane bounded by `max(|x|,|y|)lt=1` and `x ylt=1/2` is
(a) `1/2+ln2` `s qdot` `u n i t s`
(b) `3+ln2` `s qdot` `u n i t s`
(c)`(31)/4` `s qdot` `u n i t s`
(d) `1+2ln2` `s qdot` `u n i t s`
View SolutionThe area of the figure bounded by the parabola `(y-2)^(2)=x-1,` the tangent to it at the point with the ordinate y=3, and the x-axis is
View SolutionThe area of the loop of the curve `a y^2=x^2(a-x)` is
View SolutionThe area of the region bounded by `x=0,y=0,x=2,y=2,ylt=e^x` and `ygeq1nx` is (a) `6-41n2s qdotu n i t s` (b) `41n2-2s qdotu n i t s` `21n2-4s qdotu n i t s` (d) `6-21n2s qdotu n i t s`
View SolutionIf `f(x)=sinx ,AAx in [0,pi/2],f(x)+f(pi-x)=2,AAx in (pi/2,pi]a n df(x)=f(2pi-x),AAx in (pi,2pi],` then the area enclosed by `y=f(x)` and the x-axis is
(a)`pi` sq `dot` units
(b) `2pi` sq `dot` units
(c) `2` sq `dot` units
(d) `4`sq `dot` units
View SolutionThe area enclosed by the curve `y=sqrt(4-x^2),ygeqsqrt(2)sin((xpi)/(2sqrt(2)))` , and the x-axis is divided by the y-axis in the ratio.
(a) `(pi^2-8)/(pi^2+8)`
(b) `(pi^2-4)/(pi^2+4)`
(c)`(pi-4)/(pi-4)`
(d) `(2pi^2)/(2pi+pi^2-8)`
View SolutionThe area bounded by the curves `y=xe^x,y=xe^-x` and the lines `x=1` is
View SolutionThe area enclosed by the curves `xy^2=a^2(a-x)` and `(a-x)y^2=a^2x` is
View SolutionThe area bounded by the loop of the curve `4y^2=x^2(4-x^2)` is (a)7/3 sq. units (b) `8/3s qdotu n i t e s` `(11)/3s qdotu n i t s` (d) `(16)/3s qdotu n i t s`
View SolutionThe area bounded by the curve `f(x)=x+sinx` and its inverse function between the ordinates `x=0a n dx=2pi` is `4pis qdotu n i t s` (b) `8pis qdotu n i t s` `4s qdotu n i t s` (d) `8s qdotu n i t s`
View SolutionThe area enclosed by the curve `y=sinx+cosxa n dy=|cosx-sinx|` over the interval `[0,pi/2]` is `(a)4(sqrt(2)-2)` (b) `2sqrt(2)` (`sqrt(2)` -1) `(c)2(sqrt(2)` +1) (d) `2sqrt(2)(sqrt(2)+1)`
View SolutionFor which of the following values of `m` is the area of the regions bounded by the curve `y=x-x^2` and the line `y=m x` equal `9/2?` (a) `-4` (b) `-2` (c) 2 (d) 4
View SolutionThe area of the region bounded by the curve `y=e^(x)` and lines x=0 and y=e is
View SolutionFind the area bounded by the curves `x^2+y^2=4, x^2=-sqrt2 y` and `x=y`
View SolutionFor a point `P` in the plane, let `d_1(P)a n dd_2(P)` be the distances of the point `P` from the lines `x-y=0a n dx+y=0` respectively. The area of the region `R` consisting of all points `P` lying in the first quadrant of the plane and satisfying `2lt=d_1(P)+d_2(P)lt=4,` is
View SolutionIf `a (a >0)` is the value of parameter for each of which the area of the figure bounded by the straight line `y=(a^2-a x)/(1+a^4)` and the parabola `y=(x^2+2a x+3a^2)/(1+a^4)` is the greatest, then the value of `a^4` is___
View SolutionConsider two curves `C_1: y=1/x a n dC_2: y=1nx` on the `x y` plane. Let `D_1` denotes the region surrounded by `C_1,C_2,` and the line `x=1a n dD_2` denotes the region surrounded by `C_1,C_2` and the line `x=adot` If `D_1=D_2,` then the sum of logarithm of possible value of `a` is _____________
View SolutionFind the area bounded by `y^2lt=4x ,x^2+y^2geq2x ,a n dxlt=y+2` in the first quadrant.
View SolutionFind the area of the region `R` which is enclosed by the curve `ygeqsqrt(1-x^2)` and max `{|x|,|y|}lt=4.`
View SolutionFind the area of the region enclosed by the curves `y=xlogx` and `y=2x-2x^2dot`
View SolutionFind the area of the region `{(x , y): y^2lt=4x ,4x^2+4y^2lt=9}`
View SolutionFind the area of the figure bounded by the parabolas `x=-2y^2, x=1-3y^2dot`
View SolutionFind the area bounded by `y=1/(x^2-2x+2)` and x-axis.
View SolutionFind the area bounded by `x=2y-y^2` and the `y-a x i s`.
View SolutionFind the area bounded by `y=sin^(-1)x ,y=cos^(-1)x` ,and the `X`-axis.
View SolutionDraw a rough sketch of the curve y=`(x-1)^2(x-2)(x-3)^3`
View SolutionFind the area bounded by (a) `y = (log)_e|x|a n dy=0` (b) `y=|(log)_e|x||a n dy=0`
View SolutionSketch the curves and identity the region bounded by `x=1/2,x=2,y=lnx ,a n dy=2^xdot` Find the area of this region.
View SolutionSketch the region bounded by the curves `y=x^(2) and y=(2)/(1+x^(2))`. Find the area.
View SolutionFind the area of the region bounded by the curve C : y=tan x ,tangent drawn to C at x=pi/4, and the x-axis.
View SolutionCompute the area of the region bounded by the curves `y=e x(log)_e xa n dy=(logx)/(e x)`
View Solution`A O B` is the positive quadrant of the ellipse `(x^2)/(a^2)+(y^2)/(b^2)=1` which has `O A=a ,O B=b` . Then find the area between the arc `A B` and the chord `A B` of the ellipse.
View SolutionFind the area bounded by the curves y=sin x and y=cos x between two consecutive points of the intersection.
View SolutionIn what ratio does the x-axis divide the area of the region bounded by the parabolas `y=4x-x^2a n dy=x^2-x ?`
View SolutionConsider a square with vertices at `(1,1)(-1,1)(-1,-1)and(1,-1).` Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.
View SolutionFind the area bounded by `y=x^3-x and `y=`x^2+xdot`
View SolutionFind the area, lying above the x=axis and included between the circle `x^2+y^2=8x` and the parabola `y^2=4xdot`
View SolutionConsider the region formed by the lines `x=0,y=0,x=2,y=2.` If the area enclosed by the curves `y=e^x a n dy=1nx ,` within this region, is being removed, then find the area of the remaining region.
View SolutionFind the area bounded by the curve `y=(x-1)(x-2)(x-3)` lying between the ordinates `x=0a n dx=3.`
View SolutionFind the area bounded by the parabola `y=x^2+1` and the straight line `x+y=3.`
View SolutionFind the area of the closed figure bounded by the curves `y=sqrt(x),y=sqrt(4-3x) and y=0`
View SolutionFind the area of the smaller part of the circle `x^2+y^2=a^2` cut off by the line `x=a/(sqrt(2))`
View SolutionThe area enclosed by the curve `c : y=xsqrt(9-x^2) (xgeq0)` and the x-axis is________
View SolutionThe area bounded by the curves `y=x(x-3)^2a n dy=x` is________ (in sq. units)
View SolutionColumn I, Column II Area enclosed , q. 1. sq. units The smaller area included between the curves `sqrt(x)+sqrt(|y|)=1` and `|x|+|y|=1` , r. 4 sq. units Area bounded by the curves `y=[(x^2)/(64)+2](w h e r e[dot]d e not e s` the greatest integer function), `y=x-1a n dx=0` above the x-axis., s. 2/3 sq. units
View SolutionConsider two regions:` ` ` R_1:` Point `P` is nearer to `(1,0)` then to `x=-1.` `R_2:` Point `P` is nearer to `(0,0)` then to `(8,0).` Then which of the following statements are true: `Statement 1`: The area of the region common to `R_1 and R_2` is `(128)/3s q dotu n i t s`. ` ``Statement 2` : The area bounded by `x=4sqrt(y) and y=4` is `(32)/3s qdotu n i t s`.
View SolutionStatement 1 : The area bounded by `2geqm a xdot{|x-y|,|x|y"|"}` is 8 sq. units. Statement 2 : The area of the square of side length 4 is 16 sq. units.
View SolutionStatement 1 : The area enclosed between the parabolas `y^2-2y+4x+5=0a n dx^2+2x-y+2=0` is same as that of bounded by curves `y^2=-4xa n dx^2=y` . Statement 2 : Shifting of origin to point `(h , k)` does not change the bounded area.
View SolutionIf the area bounded by the corve `y=x^(2)+1, y=x` and the pair of lines `x^2+y^2+2xy-4x-4y+3=0` is K units, then the area of the region bounded by the curve `y=x^2+1,y=sqrt(x-1)` and the pair of lines `(x+y-1)(x+y-3)=0` is
View SolutionLet `S` be the area bounded by the curve `y=sinx(0lt=xlt=pi)` and the x-axis and `T` be the area bounded by the curves `y=sinx(0lt=xlt=pi/2),y=acosx(0lt=xlt=pi/2),` and the x-axis `(w h e r ea in R^+)` The value of `(3a)` such that `S : T=1:1/3` is______
View SolutionLet `C` be a curve passing through `M(2,2)` such that the slope of the tangent at anypoint to the curve is reciprocal of the ordinate of the point. If the area bounded by curve C and line x=2 is A ,then the value of `(3A)/2`i s__`
View SolutionLet `f(x)` be continuous function given by `f(x)={2x ,|x|lt=1`and `x^2+a x+b ,|x|>1}dot`
Find the area of the region in the third quadrant bounded by the curves `x=-2y^2a n dy=f(x)` lying on the left of the line `8x+1=0.`
View SolutionLet `C_1C_2` be the graphs of the functions `y=x^2` and `y=2x ,` respectively, where `0lt=xlt=1.` Let `C_3` be the graph of a function `y=f(x),` where `0lt=xlt=1, f(0) =0.` For a point `P` on `C_1,` let the lines through `P ,` parallel to the axis, meet `C_2` and `C_3` at `Q` and `R ,` respectively (see Figure). If for every position of `P(onC_1),` the areas of the shaded regions `OPQ` and `ORP` are equal, determine the function `f(x)`
View SolutionFind the area bounded by the curves `x^2 = y`, `x^2 = -y` and `y^2 = 4x -3`
View SolutionThe area of the region bounded by the curves `y=x^(2),y=|2-x^(2)|` and y=2 which lies to the right of the line x=1, is
View SolutionAt freezing point of a solution there is always
View SolutionThe area bounded by the curves `y=|x|-1a n dy=-|x|+1` is 1 sq. units (b) 2 sq. units `2sqrt(2)` sq. units (d) 4 sq. units
View SolutionIf the area bounded by the curve y=f(x), x-axis and the ordinates x=1 and x=b is (b-1) `sin`(3b+4), then find f(x).
View SolutionThe area bounded by the parabolas `y=(x+1)^2` and `y=(x-1)^2a n dy=(x-1)^2` and the line `y=1/4` is 4 sq. units (b) 1/6 sq. units 4/3 sq. units (d) 1/3 sq. units
View SolutionThe area bounded by the curves `y=sqrt(x),2y+3=x ,` and x-axis in the 1st quadrant is (A) 18 sq. units (B) `(27)/4` sq.units (C) `4/3` sq.units (D) 9 sq. units
View SolutionFind the area bounded by `y=tan^(-1)x , y=cot^(-1)x ,`and y-axis in the first quadrant.
View Solutionthe equation to the director circle of `(x^2)/6+(y^2)/4=1` is
View SolutionFind the area bounded by `y=log_e x , y=-log_e x ,y=log_e(-x),a n dy=-log_e(-x)dot`
View Solutionthe area of region for which `0 lt y lt 3 - 2x-x^2` and `x gt 0` is
View SolutionThe area common to regions `x^2+y^2-2xlt=0` and `ygeq sin (pix/2)
View SolutionDraw the rough sketch of the curve `y=x^(4)-x^(2)`.
View Solution`f(x)` is a continuous and bijective function on `Rdot` If `AAt in R ,` then the area bounded by `y=f(x),x=a-t ,x=a ,` and the x-axis is equal to the area bounded by `y=f(x),x=a+t ,x=a ,` and the x-axis. Then prove that `int_(-lambda)^lambdaf^(-1)(x)dx=2alambda(gi v e nt h a tf(a)=0)dot`
View SolutionFind the continuous function `f` where `(x^4-4x^2)lt=f(x)lt=(2x^2-x^3)` such that the area bounded by `y=f(x),y=x^4-4x^2dot` then y-axis, and the line `x=t ,` where `(0lt=tlt=2)` is `k` times the area bounded by `y=f(x),y=2x^2-x^3`,y-axis , and line `x=t(w h e r e0lt=tlt=2)dot`
View SolutionFind the area bounded by the curves `y=-x^2+6x-5,y=-x^2+4x-3,` and the straight line `y=3x-15a n d` lying right to `x=1.`
View SolutionFind the value of `a` where `(a >2)` for which the reciprocal of the area enclosed between `y=1/(x^2),y=1/(4(x-1)),x=2,a n dx=a` is `a` itself and for what values of `b in (1,2),` the area of the figure bounded by the lines `x=ba n dx=2i s1-1/bdot`
View Solutionif `A_1,A_2,A_3,....A_100 `are set of `A_1 sup A_2 sup A_3 sup A_4.....sup A_100` `n(A_i)=i+2` , `nn_(i=3)^100A_i` =
View SolutionDraw the rough sketch of `y^2+1=x ,\ xlt=2.` Find the area enclosed by the curve and the line `x=2.`
View SolutionEach question has four choices a,b,c and d, out of which only one is correct. Each question contains STATEMENT 1 and STATEMENT 2. If both the statements are TRUE and STATEMENT 2 is the correct explanation of STATEMENT 1 If both the statements are TRUE but STATEMENT 2 is NOT the correct explanation of STATEMENT 1. If STATEMENT 1 is TRUE and STATEMENT 2 is FALSE. If STATEMENT 1 is FALSE and STATEMENT 2 is TRUE. Statement 1 : The area bounded by `y=e^x , y=0a n dx=0` is 1 sq. unites. Statement 2 : The area bounded by `y=(log)_e x ,x=0,a n dy=0` is 1 sq. units.
View SolutionIf `A_1,A_2, A_3,..`are sets such that `n(A_i)=101-i`, `A_1 sup A_2 sup A_3 sup ...supA_100` and `A=nn_(i=5)^100 A_i` then n(A) is equal to
View SolutionLet `A(k)` be the area bounded by the curves `y=x^2-3` and `y=k x+2` The range of `A(k)` is `((10sqrt(5))/3,oo)` The range of `A(k)` is `((20sqrt(5))/3,oo)` If function `kvecA(k)` is defined for `k in [-2,oo` ), then `A(k)` is many-one function. The value of `k` for which area is minimum is `1.`
View Solution`int (ax^2+bx+c)dx` =
View Solution
All Questions questions and complete solutions for chapter APPLICATION OF INTEGRALS of CENGAGE MATHS (ENGLISH) of Class 12