Question

Let ${\displaystyle C_1{C}_2}$
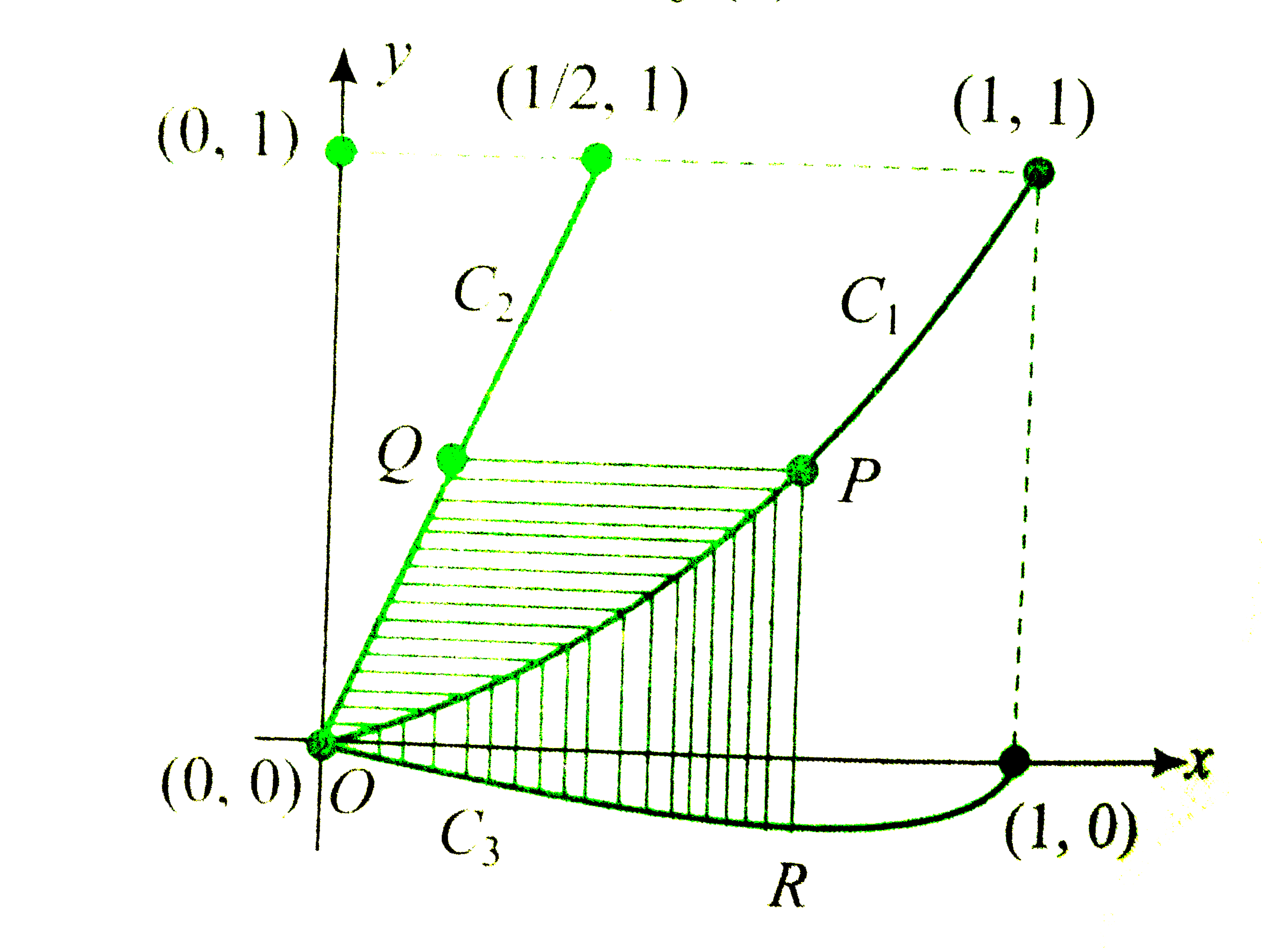
be the graphs of the functions ${\displaystyle y=x^2}$ and ${\displaystyle y=2x,}$
respectively, where ${\displaystyle 0\le x\le 1.}$
Let ${\displaystyle C_3}$
be the graph of a function ${\displaystyle y=f\left(x\right),}$
where ${\displaystyle 0\le x\le 1,f\left(0\right)=0.}$
For a point ${\displaystyle P}$ on ${\displaystyle C_1,}$
let the lines through ${\displaystyle P,}$
parallel to the axis, meet ${\displaystyle C_2}$ and ${\displaystyle C_3}$
at ${\displaystyle Q}$ and ${\displaystyle R,}$
respectively (see Figure). If for every position of ${\displaystyle P\left(on{C}_1\right),}$
the areas of the shaded regions ${\displaystyle OPQ}$ and ${\displaystyle ORP}$
are equal, determine the function ${\displaystyle f\left(x\right)}$

Explanation

To solve the problem, we need to determine the function $$f\left(x\right)$$ such that the areas of the regions $$OPQ$$ and $$ORP$$ are equal for any point $$P$$ on the curve $$C_1$$ defined by $$y=x^2$$.

1. Identify the curves:
- The curves are given as:
- \( C_1: y = x^2 \)
- \( C_2: y = 2x \)
- \( C_3: y = f(x) \)
- The domain for \( x \) is \( 0 < x < 1 \).

2. Find the coordinates of points \( P \), \( Q \), and \( R \):
- Let \( P \) be a point on \( C_1 \) at \( (x, x^2) \).
- The line through \( P \) parallel to the y-axis meets \( C_2 \) at point \( Q \) and \( C_3 \) at point \( R \).
- The coordinates of \( Q \) are \( (x, 2x) \) and the coordinates of \( R \) are \( (x, f(x)) \).

3. Calculate the areas of regions \( OPQ \) and \( ORP \):
- The area of triangle \( OPQ \) can be calculated as:
\( \text{Area}_{OPQ} = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times x \times (2x - x^2) = \frac{1}{2} x (2x - x^2) = \frac{1}{2} (2x^2 - x^3) \)
- The area of triangle \( ORP \) is:
\( \text{Area}_{ORP} = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times x \times (f(x) - x^2) = \frac{1}{2} x (f(x) - x^2) \)

4. Set the areas equal:
- Since the areas are equal, we have:
\( \frac{1}{2} (2x^2 - x^3) = \frac{1}{2} x (f(x) - x^2) \)
- Simplifying this gives:
\( 2x^2 - x^3 = x (f(x) - x^2) \)
- Dividing both sides by \( x \) (for \( x \neq 0 \)):
\( 2x - x^2 = f(x) - x^2 \)
- Rearranging gives:
\( f(x) = 2x \)

5. Final expression for \( f(x) \):
- Thus, we find that:
\( f(x) = 2x \)

Conclusion:
The function \( f(x) \) that satisfies the condition of equal areas for the regions \( OPQ \) and \( ORP \) is:
\( f(x) = 2x \)