Complete Solutions to REASONING TYPE of chapter THREE-DIMENSIONAL GEOMETRY of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | THREE-DIMENSIONAL GEOMETRY |
| CENGAGE NEW | REASONING TYPE |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
Statement 1 : Lines `vecr= hati-hatj+ lamda (hati+hatj-hatk) and vecr= 2hati-hatj+ mu (hati+hatj-hatk)` do not intersect.
Statement 2 : Skew lines never intersect.
View SolutionStatement 1 : Lines `vecr=hati+hatj-hatk+lamda(3hati-hatj) and vecr=4hati-hatk+ mu (2hati+ 3hatk)` intersect.
Statement 2 : If `vecbxxvecd=vec0`, then lines `vecr=veca+lamdavecb and vecr= vecc+lamdavecd` do not intersect.
View SolutionThe equation of two straight lines are `(x-1)/2=(y+3)/1=(z-2)/(-3)a n d(x-2)/1=(y-1)/(-3)=(z+3)/2dot` Statement 1: the given lines are coplanar. Statement 2: The equations `2r-s=1,r+3s=4a n d3r+2s=5` are consistent.
View SolutionStatement 1: A plane passes through the point `A(2,1,-3)dot` If distance of this plane from origin is maximum, then its equation is `2x+y-3z=14.`
Statement 2: If the plane passing through the point `A( vec a)` is at maximum distance from origin, then normal to the plane is vector ` vec adot`
View SolutionStatement 1: Line `(x-1)/1=(y-0)/2=(z+2)/(-1)` lies in the plane `2x-3y-4z-10=0.` Statement 2: if line ` vec r= vec a+lambda vec b` lies in the plane ` vec rdot vec c=n(w h e r en` is scalar`),t h e n vec bdot vec c=0.`
View SolutionStatement 1: Let `theta` be the angle between the line `(x-2)/2=(y-1)/(-3)=(z+2)/(-2)` and the plane `x+y-z=5.` Then `theta=sin^(-1)(1//sqrt(51))dot` Statement 2: The angle between a straight line and a plane is the complement of the angle between the line and the normal to the plane.
View SolutionStatement 1: let `A( vec i+ vec j+ vec k)a n dB( vec i- vec j+ vec k)` be two points. Then point `P(2 vec i+3 vec j+ vec k)` lies exterior to the sphere with `A B` as its diameter. ,
Statement 2: If `Aa n dB` are any two points and `P` is a point in space such that ` vec(PA).vec(PB) >0` , then point `P` lies exterior to the sphere with `A B` as its diameter.
View SolutionStatement 1: there exists a unique sphere which passes through the three non-collinear points and which has the least radius. Statement 2: The centre of such a sphere lies on the plane determined by the given three points.
View SolutionStatement 1: There exist two points on the `(x-1)/1=y/(-1)=(z+2)/2` which are at a distance of 2 units from point `(1,2,-4)dot` Statement 2: Perpendicular distance of point `(1,2,-4)` form the line `(x-1)/1=y/(-1)=(z+2)/2` is 1 unit.
View SolutionFor an ideal gas, an illustration of three different paths `A(B+C)` and `(D+E)` from an initial state `P_(1), V_(1), T_(1)` to a final state `P_(2), V_(2),T_(1)` is shown in the given figure.
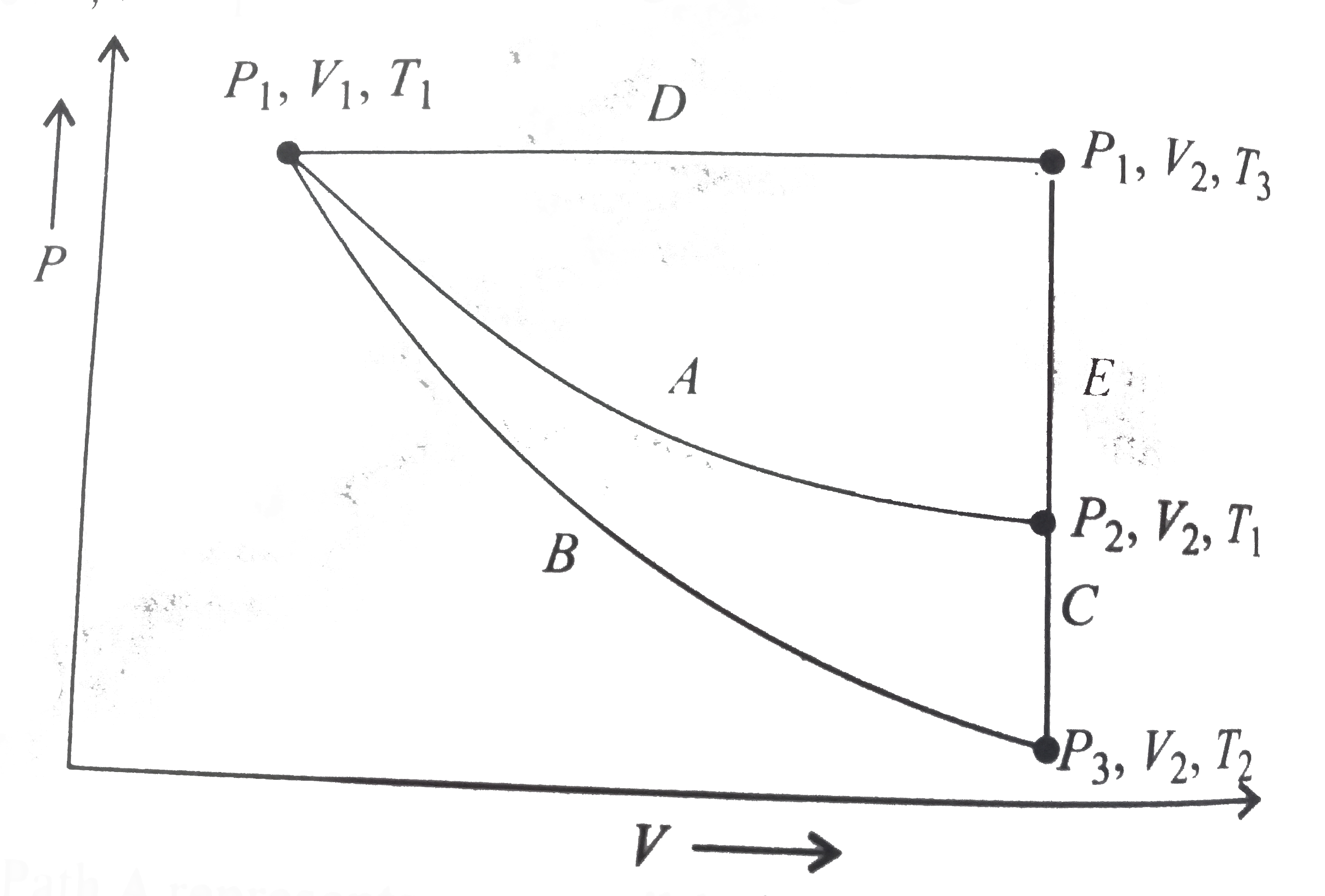
Path `A` represents a reversible isothermal expansion form `P_(1),V_(1)` to `P_(2),V_(2)`, Path `(B+C)` represents a reversible adiabatic expansion `(B)` from `P_(1),V_(1),T_(1)to P_(3),V_(2),T_(2)` followed by reversible heating the gas at constant volume `(C)`from `P_(3),V_(2),T_(2)` to `P_(2),V_(2),T_(1)`. Path `(D+E)` represents a reversible expansion at constant pressure `P_(1)(D)` from `P_(1),V_(1),T_(1)` to `P_(1),V_(2),T_(3)` followed by a reversible cooling at constant volume `V_(2)(E)` from `P_(1),V_(2),T_(3) to P_(2),V_(2),T_(1)`.
What is `DeltaS` for path `(D +E)`?
View Solution
REASONING TYPE questions and complete solutions for chapter THREE-DIMENSIONAL GEOMETRY of CENGAGE MATHS (ENGLISH) of Class 12
All Exercises from CENGAGE NEW Class 12 MATHS THREE-DIMENSIONAL GEOMETRY
- ARCHIVES INTEGER TYPE
- ARCHIVES LINKED COMPREHENSION TYPE
- ARCHIVES MATRIX-MATCH TYPE
- ARCHIVES MULTIPLE CORRECT ANSWERS TYPE
- ARCHIVES REASONING TYPE
- ARCHIVES SINGLE CORRECT ANSWER TYPE
- ARCHIVES SUBJECTIVE TYPE
- CONCEPT APPLICATION EXERCISE 3.1
- CONCEPT APPLICATION EXERCISE 3.2
- CONCEPT APPLICATION EXERCISE 3.3
- CONCEPT APPLICATION EXERCISE 3.4
- ILLUSTRATION
- INTEGER TYPE
- LINKED COMPREHENSION TYPE
- MATRIX-MATCH TYPE
- MULTIPLE CORRECT ANSWER TYPE
- REASONING TYPE
- SINGLE CORRECT ANSWER TYPE
- SUBJECTIVE TYPE