Complete Solutions to JEE ADVANCED of chapter DEFINITE INTEGRATION of Class 12 book with complete answers and questions

Let `f` be a non-negative function defined on the interval `[0,1]`. If `int_0^xsqrt(1-(f^(prime)(t))^2)dt=int_0^xf(t)dt ,0lt=xlt=1,a n d \ f(0)=0`, then

The value of `int_0^1(x^4(1-x)^4)/(1+x^2)\ dx` is

Let `f` be a real-valued function defined on the inverval `(-1,1)` such that `e^(-x)f(x)=2+int_0^xsqrt(t^4+1)dt ,` for all, `x in (-1,1)a n dl e tf^(-1)` be the inverse function of `fdot` Then `(f^(-1))^'(2)` is equal to 1 (b) `1/3` (c) `1/2` (d) `1/e`

The valued of `int_(sqrt(In2))^(sqrt(In3)) (x sinx^(2))/(sinx^(2)+sin(In 6-x^(2)))dx` is

Let `f:[-1,2]->[0,oo)` be a continuous function such that `f(x)=f(1-x)fora l lx in [-1,2]dot` Let `R_1=int_(-1)^2xf(x)dx ,` and `R_2` be the area of the region bounded by `y=f(x),x=-1,x=2,` and the x- axis . Then `R_1=2R_2` (b) `R_1=3R_2` (c) `2R_1=R_2` (d) `3R_1=R_2`

Let `f:[1/2,1]->R` (the set of all real numbers) be a positive, non-constant, and differentiable function such that `f^(prime)(x)<2f(x))a n df(1/2)=1` . Then the value of `int_(1/2)^1f(x)dx` lies in the interval (a) `(2e-1,2e)` (b) `(3-1,2e-1)` `((e-1)/2,e-1)` (d) `(0,(e-1)/2)`

Let `f:[0,2]vecR` be a function which is continuous on [0,2] and is differentiable on (0,2) with `f(0)=1` `L e t :F(x)=int_0^(x^2)f(sqrt(t))dtforx in [0,2]dotIfF^(prime)(x)=f^(prime)(x)` . for all `x in (0,2),` then `F(2)` equals `e^2-1` (b) `e^4-1` `e-1` (d) `e^4`

`int_((pi)/4)^((pi)/2)(2cosecx)^17` dx

Let `f prime(x)=(192x^3)/(2+sin^4 pix)` for all `x in RR` with `f(1/2)=0.` If `mlt=int_(1/2)^1f(x)dxlt=M` then the possible values of m and M are (i) `m=13,M= 24` (ii)` m=1/4,M=1/2` (iii) `m=-11,M = 0` (iv) `m=1,M=12`

Evaluate: `int_(-pi//2)^(pi//2)(x^2cosx)/(1+e^x)dx`

If `I_n=int_(-pi)^(pi) \ (sinnx)/((1+pi^x) \ sinx) \ dx, n=0,1,2,......` then which one of the following is not true ?

about to only mathematics

Let `S` be the area of the region enclosed by `y=e^-(x^2),y=0,x=0,a n dx=1.` Then `Sgeq1/e` (b) `Sgeq1-1/e` (c) `Slt=1/4(1+1/(sqrt(e)))` (d) `Slt=1/(sqrt(2))+1/(sqrt(e))(1-1/(sqrt(2)))`

Find `a` for which `lim_(n->oo) (1^a+2^a+3^a+...+n^a)/((n+1)^(a-1)[(na+1)+(na+2)+...+(na+n)])=1/60`

Let `f:[a,b]to[1,oo)` be a continuous function and let `g:RtoR` be defined as
`g(x)={(0,"if",xlta),(int_(a)^(x)f(t)dt,"if",alexleb),(int_(a)^(b)f(t)dt,"if",xgtb):}` Then

Let `f:(0,oo) in R` be given
`f(x)=overset(x)underset(1//x)int e^(t+(1)/(t))(1)/(t)dt`, then

The option(s) with the values of `aa n dL` that satisfy the following equation is (are) `(int0 4pie^t(s in^6a t+cos^4a t)dt)/(int0pie^t(s in^6a t+cos^4a t)dt)=L` `a=2,L=(e^(4pi)-1)/(e^(pi)-1)` (b) `a=2,L=(e^(4pi)+1)/(e^(pi)+1)` `a=4,L=(e^(4pi)-1)/(e^(pi)-1)` (d) `a=4,L=(e^(4pi)+1)/(e^(pi)+1)`

Let `f(x)=7tan^8x+7tan^6x-3tan^4x-3tan^2x` for all `x in (-pi/2,pi/2)` . Then the correct expression (s) is (are) (a) `int_0^(pi/4)xf(x)dx=1/(12)` (b) `int_0^(pi/4)f(x)dx=0` (c) `int_0^(pi/4)xf(x)=1/6` (d) `int_0^(pi/4)f(x)dx=1/(12)`

find the period of sin`(x/2)-cos(x/3)` is

Let `f: Rvec(0,1)` be a continuous function. Then, which of the following function (s) has (have) the value zero at some point in the interval (0,1)? `e^x-int_0^xf(t)sintdt` (b) `f(x)+int_0^(pi/2)f(t)sintdt` `x-int_0^(pi/2-x)f(t)costdt` (d) `x^9-f(x)`

If `Isum_(k=1)^(98)int_k^(k+1)(k+1)/(x(x+1))dx ,t h e n:` (a) `I<(49)/(50)` (b) `I >(log)_e 99` (c) `I >(49)/(50)` (d) `I<(log)_e 99`

If `g(x)=int_(sinx)^("sin"(2x))sin^(-1)(t)dt ,t h e n :`
(a) `g^(prime)(pi/2)=-2pi` (b) `g^(prime)(-pi/2)=-2pi` (c) `g^(prime)(-pi/2)=2pi` (d) `g^(prime)(pi/2)=2pi`

Given that for each `a epsilon(0,1),lim(hto 0^(+)) int_(h)^(1-h)t^(-a)(1-t)^(a-1)dt` exists. Let this limit be `g(a)`. In addition it is given the function `g(a)` is differentiable on`(0,1)`.
The value of `g(1/2)` is a. `(pi)/2` b. `pi` c.`-(pi)/2` d. `0`

Given that for each `a epsilon(0,1),lim(hto 0^(+)) int_(h)^(1-h)t^(-a)(1-t)^(a-1)dt` exists. Let this limit be `g(a)`. In addition it is given the function `g(a)` is differentiable on`(0,1)`.
The value of `g(1/2)` is a. `(pi)/2` b. `pi` c.`-(pi)/2` d. `0`

Let `F:RtoR` be a thrice differntiable function. Suppose that `F(1)=0,F(3)=-4` and `F'(x)lt0` for all `x epsilon(1//2,3)`. Let `f(x)=xF(x)` for all `x inR`. Then the correct statement(s) is (are)

Let `F:RtoR` be a thrice differntiable function. Suppose that `F(1)=0,F(3)=-4` and `F'(x)lt0` for all `x epsilon(1//2,3)`. Let `f(x)=xF(x)` for all `x inR`. Then the correct statement(s) is (are)

Match the terms given in Column I with the compound given in Column II.

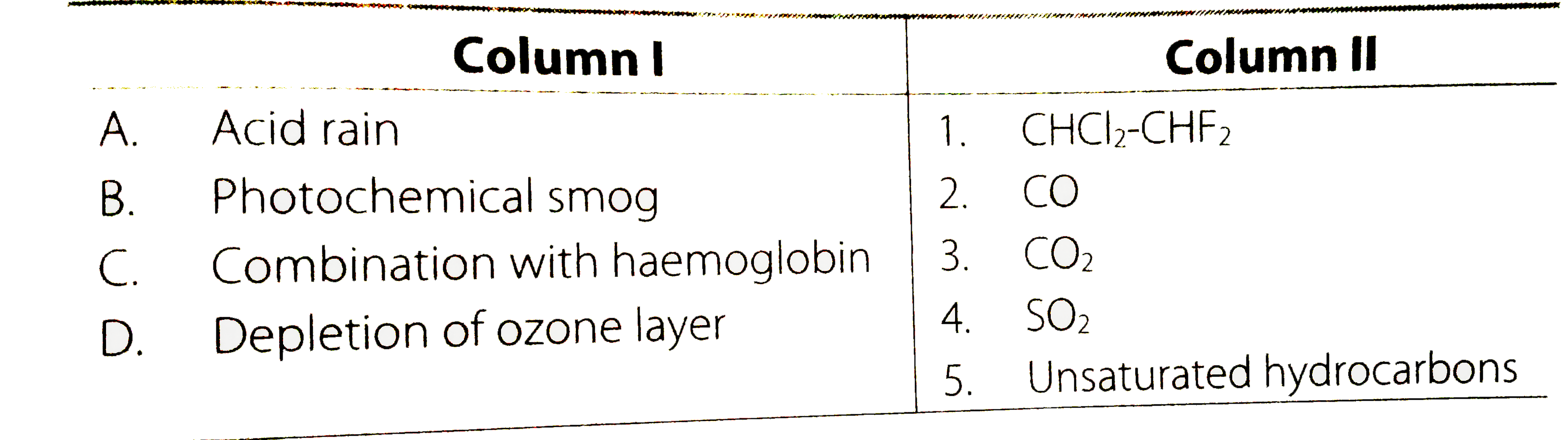
For any real number `x`, let `[x]` denote the largest integer less than or equal to `x`, Let `f` be a real-valued function defined on the interval `[-10 , 10]` be `f(x)={x-[x], if [x]` is odd, `1+[x]-x ,if[x]` is even Then the value of `(pi^2)/(10)int_(-10)^(10)f(x)cospixdx` is____

Let `y^(prime)(x)+y(x)g^(prime)(x)=g(x)g^(prime)(x),y(0),x in R ,` where `f^(prime)(x)` denotes `(dy(x))/(dx),` and `g(x)` is a given non-constant differentiable function on `R` with `g(0)=g(2)=0.` Then the value of `y(2)` is______

The value of `int_0^1 4x^3{(d^2)/(dx^2)(1-x^2)^5}dx` is

Let `f: R rarr R` be a continuous odd function, which vanishes exactly at one point and `f(1)=1/2`. Suppose that `F(x)=int_(-1)^xf(t)dt` for all `x in [-1,2]` and `G(x)=int_(-1)^x t|f(f(t))|dt` for all `x in [-1,2]`. If `lim_(x rarr 1)(F(x))/(G(x))=1/(14)`, Then the value of `f(1/2)` is

If `alpha=int_0^1(e^(9x+3tan^(-1)x))((12+9x^2)/(1+x^2))dx` where `tan^(-1)x` takes only principal values, then, find the value of `((log)_e|1+alpha|-(3pi)/4)`

Let `F(x)=int_x^[x^2+pi/6](2cos^2t)dt` for all `x in R` and `f:[0,1/2] -> [0,oo)` be a continuous function.For `a in [0,1/2]`, if F'(a)+2 is the area of the region bounded by x=0,y=0,y=f(x) and x=a, then f(0) is

Let `f: RvecR` be a function defined by `f(x)={[x],(xlt=2) \ \ (0,x >2)` where `[x]` is the greatest integer less than or equal to `xdot` If `I=int_(-1)^2(xf(x^2))/(2+f(x+1))dx , then \ the \ value \ of \ (4I-1)i s`

The total number for distinct `x epsilon[0,1]` for which `int_(0)^(x)(t^(2))/(1+t^(4))dt=2x-1` is __________.

Let `f: R -> R` be a differentiable function such that `f(0) = 0,f(pi/2)=3a n df^(prime)(0)=1.` If `g(x)=int_x^(pi/2)[f^(prime)(t)cos e ct-cottcos e ctf(t)]dt` for `x(0,pi/2],` then `(lim)_(x -> 0)g(x)=`

For each positive integer `n` , let `y_n=1/n((n+1)(n+2)dot(n+n))^(1/n)` For `x in R` let `[x]` be the greatest integer less than or equal to `x` . If `(lim)_(n->oo)y_n=L` , then the value of `[L]` is ______.

The value of the integral `int_0^(1/2)(1+sqrt(3))/(((x+1)^2(1-x)^6)^(1/4))dx` is ______.