Complete Solutions to Comprehension of chapter PROBABILITY I of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | PROBABILITY I |
| CENGAGE NEW | Comprehension |
| Number Of Questions | 14 |
| Academic Year | 2023-24 |
A shoping mall is running a scheme: Each packet of detergent SURF contains a coupon which bears letter of the word SURF, if a person buys at least four packets of detergent SURF, and produce all the letters of the word SURF, then he gets one free packet of detergent.
If a person buys 8 such packets at a time, then the number of different combinations of coupon he has is
View SolutionA shoping mall is running a scheme: Each packet of detergent SURF contains a coupon which bears letter of the word SURF, if a person buys at least four packets of detergent SURF, and produce all the letters of the word SURF, then he gets one free packet of detergent.
If person buys 8 such packets, then the probability that he gets exactly one free packets is
View SolutionA shoping mall is running a scheme: Each packet of detergent SURF contains a coupon which bears letter of the word SURF, if a person buys at least four packets of detergent SURF, and produce all the letters of the word SURF, then he gets one free packet of detergent.
If a person buys 8 such packets, then the probability that he gets two free packets is
View SolutionThere are two die A and B both having six faces. Die A has three faces marked with 1, two faces marked with 2, and one face marked with 1, two faces marked with 2, and one face marked with 3. Die B has one face marked with 1, two faces marked with 2, and three faces marked with 3. Both dices are thrown randomly once. If E be the event of getting sum of the numbers appearing on top faces equal to x and let P(E) be the probability of event E, then
P(E) is minimum when x equals to
View SolutionThere are two die A and B both having six faces. Die A has three faces marked with 1, two faces marked with 2, and one face marked with 3. Die B has one face marked with 1, two faces marked with 2, and three faces marked with 3. Both dices are thrown randomly once. If E be the event of getting sum of the numbers appearing on top faces equal to x and let P(E) be the probability of event E, then P(E) is minimum when x equals to
View SolutionThere are two die A and B both having six faces. Die A has three faces marked with 1, two faces marked with 2, and one face marked with 1, two faces marked with 2, and one face marked with 3. Die B has one face marked with 1, two faces marked with 2, and three faces marked with 3. Both dices are thrown randomly once. If E be the event of getting sum of the numbers appearing on top faces equal to x and let P(E) be the probability of event E, then
P(E) is maximum when x equal to
View SolutionA cube having all of its sides painted is cut by two horizontal, two vertical, and other two planes so as to form 27 cubes all having the same dimensions. Of these cubes, a cube is selected at random.
The probability that the cube selected has two sides painted is
View SolutionA cube having all of its sides painted is cut by two horizontal, two vertical, and other two planes so as to form 27 cubes all having the same dimensions. Of these cubes, a cube is selected at random.
The probability that the cube selected has none of its sides painted is
View SolutionA cube having all of its sides painted is cut to be two horizontal , two vertical and other two planes, so as to form 27 cubes all having the same dimesions of these cubes, a cube is selected at random.
If `P_1` be the probability that the cube selected having atleast one of its sides painted, then the value of `27P_1`, is
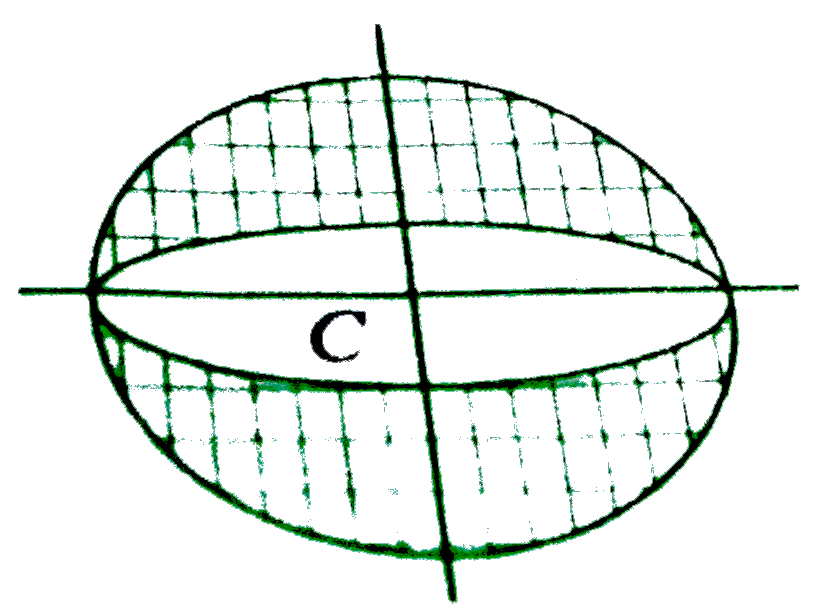
View SolutionThere are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity `2sqrt(2)//3` is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
`1 - (b^(2))/(a^(2)) = (8)/(9) or (b^(2))/(a^(2)) = (1)/(9)`
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
`p= ("Area of shaded region")/("Area of circle")`
`=(pia^(2) - piab)/(pia^(2)) = 1 - (b)/(a) = 1 - (1)/(3) = (2)/(3)`
Now, answer the following questions.
Two persons A and B agree to meet at a place between 5 and 6 pm. The first one to arrive waits for 20 min and then leave. If the time of their arrival be independant and at random, then the probability that A and B meet is
View SolutionThere are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity `2sqrt(2)//3` is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
`1 - (b^(2))/(a^(2)) = (8)/(9) or (b^(2))/(a^(2)) = (1)/(9)`
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
`p= ("Area of shaded region")/("Area of circle")`
`=(pia^(2) - piab)/(pia^(2)) = 1 - (b)/(a) = 1 - (1)/(3) = (2)/(3)`
Now, answer the following questions.

Two persons A and B agree to meet at a place between 5 and 6 pm. The first one to arrive waits for 20 min and then leave. If the time of their arrival be independant and at random, then the probability that A and B meet is
View SolutionIf the squares of a `8 xx 8` chessboard are painted either red or black at random.
The probability that all the squares in any column are of same order and that of a row are of alternating color is
View SolutionIf the squares of a `8 xx 8` chessboard are painted either red or black at random.
The probability that all the squares in any column are of same order and that of a row are of alternating color is
View SolutionIf the squares of a `8 xx 8` chess board are painted either red and black at random .The probability that not all squares is any alternating in colour is
View Solution
Comprehension questions and complete solutions for chapter PROBABILITY I of CENGAGE MATHS (ENGLISH) of Class 12