Complete Solutions to Exercise (Multiple) of chapter RELATIONS AND FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| CENGAGE NEW | Exercise (Multiple) |
| Number Of Questions | 27 |
| Academic Year | 2023-24 |
Let `f(x)=sec^(-1)[1+cos^(2)x],` where [.] denotes the greatest integer function. Then the
03:08View SolutionLet `f : R rarr[-1,oo] and f(x)= ln([|sin 2 x|+|cos 2 x|])` (where[.] is greatest integer function), then -
03:19View SolutionIf `f: RvecNuu{0},` where `f` (area of triangle joining points `P(5,0),Q(8,4)a n dR(x , y)` such that angle PRQ is a right angle `=` number of triangles, then which of the following is true? `f(5)=4` (b) `f(7)=0` `f(6, 25)=2` (d) `f(x)i snot`
08:22View SolutionThe domain of the function
`f(x)=log_(e){log_(|sinx|)(x^(2)-8x+23)-(3)/(log_(2)|sinx|)}`
contains which of the following interval (s) ?06:28View SolutionLet `f(x)=sgn(cot^(-1)x)+tan(pi/2[x]),` where `[x]` is the greatest integer function less than or equal to `x ,` then which of the following alternatives is/are true? `f(x)` is many-one but not an even function. `f(x)` is a periodic function. `f(x)` is a bounded function. The graph of `f(x)` remains above the x-axis.
07:18View Solution`f(x)=sqrt(1-sin^(2)x)+sqrt(1+tan^(2)x)` then
04:48View SolutionIf the following functions are defined from `[-1,1]to[-1,1],` select those which are not objective. `sin(s in^(-1)x)` (b) `2/pisin^(-1)(sinx)` `(sgn(x))1N(e^x)` (d) `x^3(sgn(x))`
05:07View SolutionLet `f(x)={x^2-4x+3,x<3x-4,xgeq3` `a n dg(x)={x-3,x<4x^2+2x+2,xgeq4` then which of the following is/are true? `(f+g)(3. 5)=0` `f(g(3))=3` `(fg)(2)=1` (d) `(f-g)(4)=0`
04:18View SolutionLet `f(x)="max"(1+s in x ,1,1-cosx),x in [0,2pi],a n dg(x)=max{1,|x-1|}, x in Rdot` Then `g(f(0))=1` (b) `g(f(1))=1` `f(f(1))=1` (d) `f(g(0))+1sin1`
07:18View SolutionConsider the function `y =f(x)` satisfying the condition `f(x+1/x)=x^2+1/(x^2)(x!=0)`. Then the
02:55View SolutionConsider the real-valued function satisfying `2f(sinx)+f(cosx)=xdot` then the domain of `f(x)i sR` domain of `f(x)i s[-1,1]` range of `f(x)` is `[-(2pi)/3,pi/3]` range of `f(x)i sR`
04:39View SolutionIf `f: R^+rightarrowR^+` is a polynomial function satisfying the functional equation `f(f(x))=6x=f(x), then f(17)` is equal to
05:49View Solution`f(x)=x^2-2a x+a(a+1)`,`f:[a ,oo)rightarrow[a ,oo)dot` If one of the solution of the equation `f(x)=f^(-1)(x) `is
03:13View SolutionWhich of the following function is/are periodic?
04:01View SolutionLet `f(x)=(3)/(4)x+1,f^(n)(x)` be defined as `f^(2)(x)=f(f(x)),` and for `n ge 2, f^(n+1)(x)=f(f^(n)(x))." If " lambda =lim_(n to oo) f^(n)(x),` then
06:51View Solutionlf the fundamental period of function `f(x)=sinx + cos(sqrt(4-a^2))x` is `4pi`, then the value of a is/are
03:22View Solution`f(x)=sin^(-1)[e^(x)]+sin^(-1)[e^(-x)]` where [.] greatest integer function then
03:52View Solution`[2x]-2[x]=lambda` where [.] represents greatest integer function and {.} represents fractional part of a real number then
03:06View SolutionThe set of all values of x satisfying `{x}=x[xx] " where " [xx]` represents greatest integer function `{xx}` represents fractional part of x
View SolutionThe function 'g' defined by `g(x)= sin(sin^(-1)sqrt({x}))+cos(sin^(-1)sqrt({x}))-1` (where {x} denotes the functional part function) is (1) an even function (2) a periodic function (3) an odd function (4) neither even nor odd
05:48View SolutionIf the function / satisfies the relation `f(x+y)+f(x-y)=2f(x),f(y)AAx , y in Ra n df(0)!=0` , then `f(x)i sa ne v e nfu n c t ion` `f(x)i sa nod dfu n c t ion` `Iff(2)=a ,t h e nf(-2)=a` `Iff(4)=b ,t h e nf(-4)=-b`
03:27View SolutionLet `f(x)+f(y)=f(xsqrt(1-y^2)+ysqrt(1-x^2))[f(x)` is not identically zero]. Then `f(4x^3-3x)+3f(x)=0` `f(4x^3-3x)=3f(x)` `f(2xsqrt(1-x^2)+2f(x)=0` `f(2xsqrt(1-x^2)=2f(x)`
09:00View SolutionLet `f: RvecR` be a function defined by `f(x+1)=(f(x)-5)/(f(x)-3)AAx in Rdot` Then which of the following statement(s) is/are ture? `f(2008)=f(2004)` `f(2006)=f(2010)` `f(2006)=f(2002)` `f(2006)=f(2018`
08:39View SolutionLet a function `f(x), x ne 0` be such that
`f(x)+f((1)/(x))=f(x)*f((1)/(x))" then " f(x)` can beView SolutionLet f be a differential function such that `f(x)=f(2-x)` and `g(x)=f(1 +x)` then (1) g(x) is an odd function (2) g(x) is an even function (3) graph of f(x) is symmetrical about the line x= 1 (4) `f'(1)=0`
02:16View SolutionThe figure illustrates the graph of the function `y=f(x)` defined in [-3, 2].
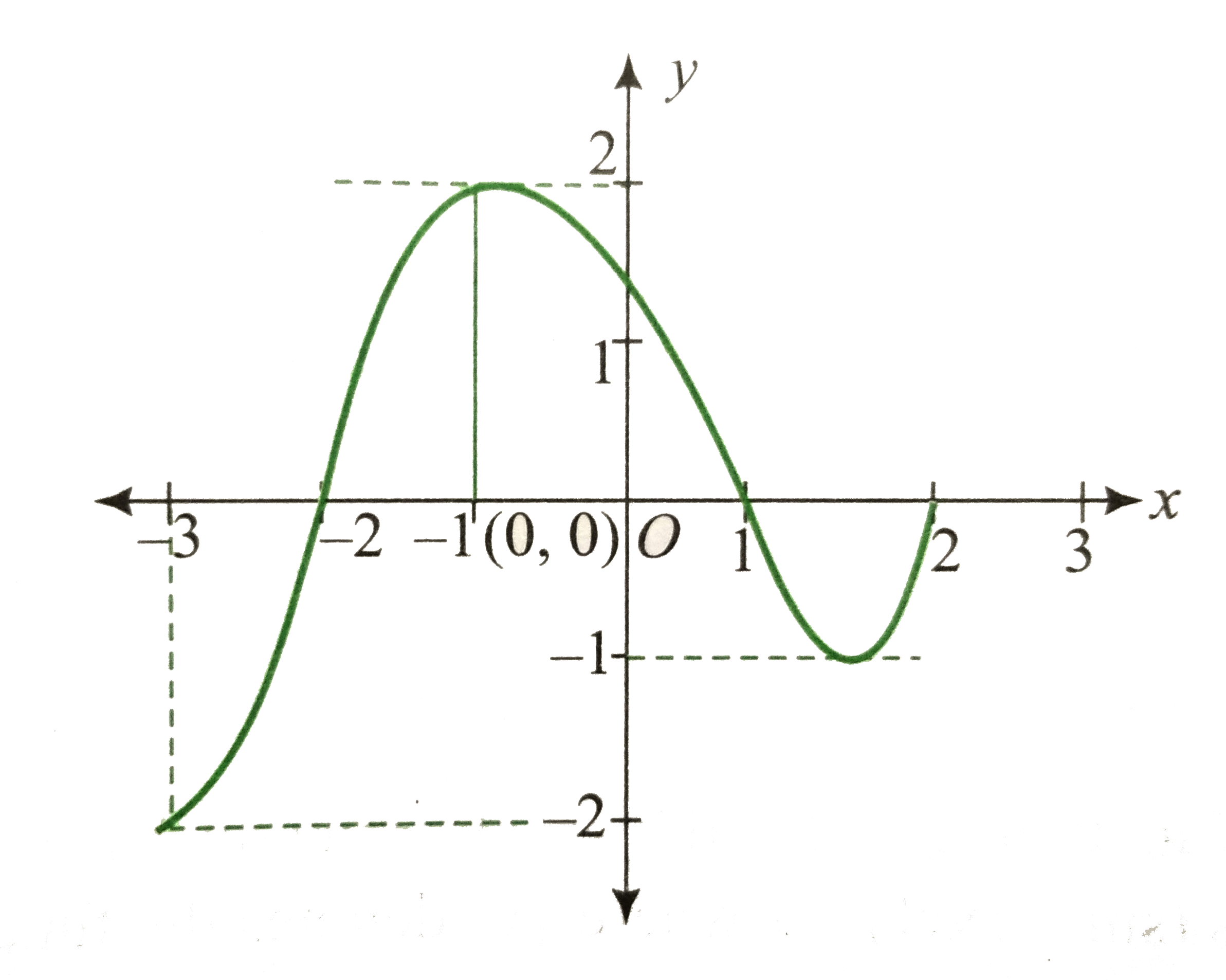
Identify the correct statement(s)?04:17View SolutionIf graph of a function `f(x)` which is defined in [-1, 4] is shown in the following figure then identify the correct statement(s).
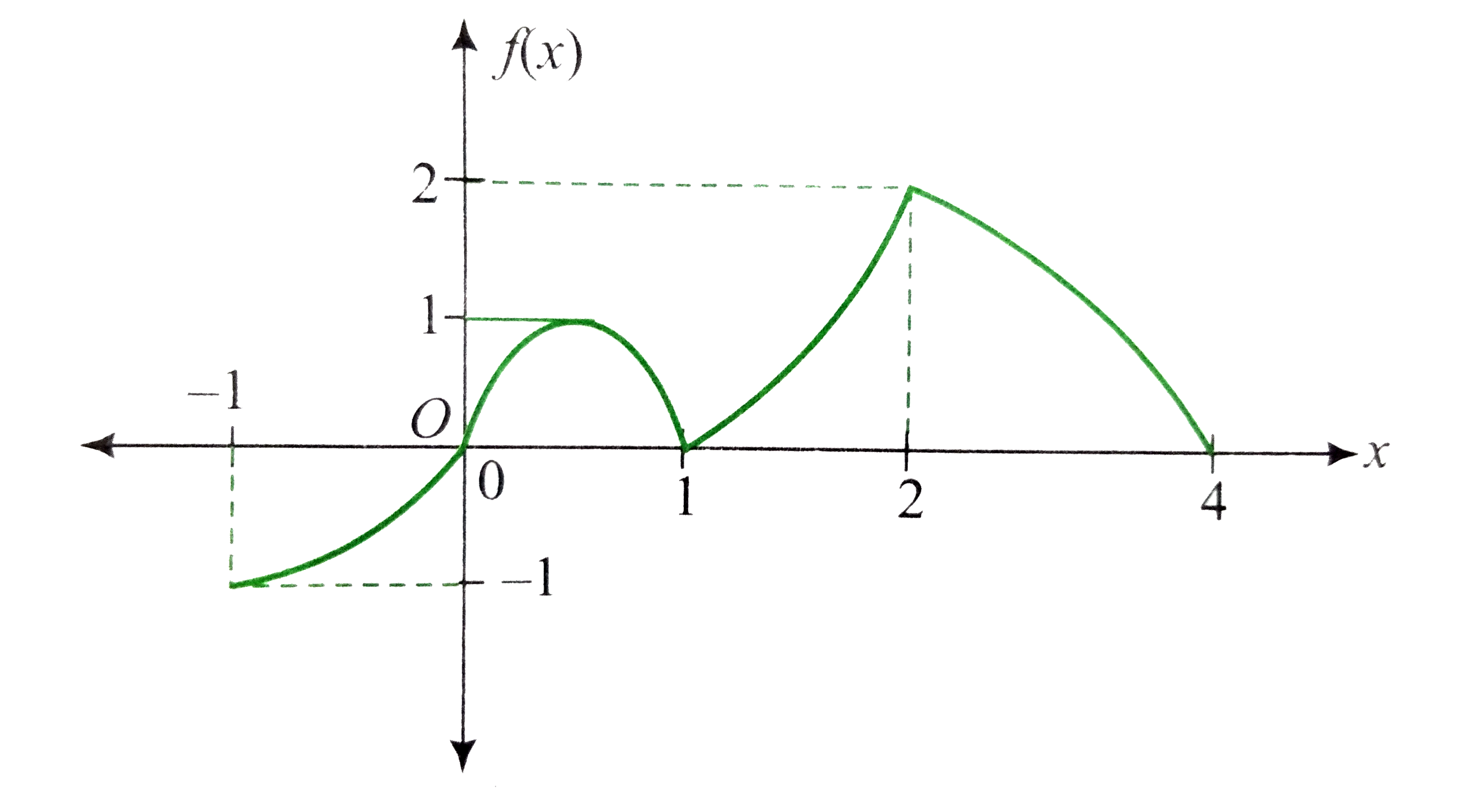 02:56View Solution
02:56View Solution
Exercise (Multiple) questions and complete solutions for chapter RELATIONS AND FUNCTIONS of CENGAGE MATHS (HINGLISH) of Class 12
All Exercises from CENGAGE NEW Class 12 MATHS RELATIONS AND FUNCTIONS
- Examples
- Exercise (Comprehension)
- Exercise (Matrix)
- Exercise (Multiple)
- Exercise (Numerical)
- Exercise (Single)
- Exercise 1.1
- Exercise 1.10
- Exercise 1.11
- Exercise 1.12
- Exercise 1.13
- Exercise 1.14
- Exercise 1.15
- Exercise 1.2
- Exercise 1.3
- Exercise 1.4
- Exercise 1.5
- Exercise 1.6
- Exercise 1.7
- Exercise 1.8
- Exercise 1.9
- JEE Previous Year
- Solved Examples And Exercises
