Complete Solutions to Exercise 2.1 of chapter LIMITS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | LIMITS |
| CENGAGE NEW | Exercise 2.1 |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
Evaluate: `("lim")_(xvec-2^+)` `(x^2-1)/(2x+4)`
02:02View SolutionEvaluate : `("lim")_(xvec2^+)` `([x-2])/("log"(x-2))` , where [.] represents the greatest integer function.
02:43View SolutionEvaluate: `("lim")_(xvec0)` `(sin[cosx])/(1+[cosx])([dot]` denotes the greatest integer function).
02:35View SolutionIf `f(x)={(x-|x|)/x ,x!=0 ,x=0,s howt h a t("lim")_(xto0)` `f(x)` does not exist.
02:48View SolutionShow that `("lim")_(xto0)` (e^ (1/x)+1 / e^ (1/x)-1) does not exist
03:55View Solution`lim_(xto0)(3x+|x|)/(7x-5|x|)`
02:30View SolutionIf `f(x)={{:(x","" "xlt0),(1","" "x=0),(x^(2)","" "xgt0):}," then find " lim_(xto0) f(x)"` if exists.
02:42View SolutionConsider the following graph of the function y=f(x). Which of the following is//are correct?
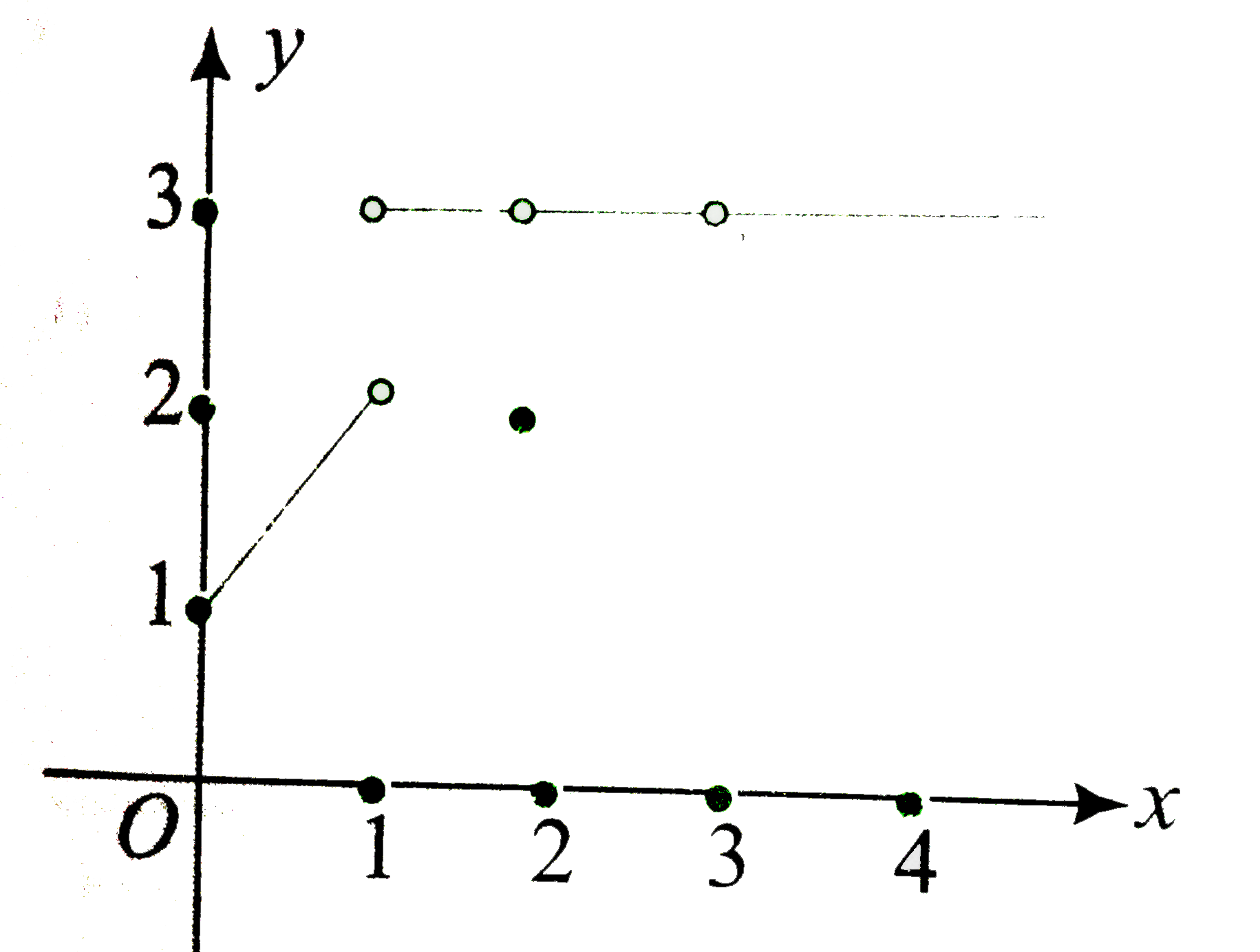
`(a) lim_(xto1) f(x)` does not exist.
`(b) lim_(xto2)f(x)` does not exist.
`(c) lim_(xto3) f(x)=3.`
`(d)lim_(xto1.99) f(x)`exists.04:44View SolutionEvaluate `lim_(x to 0) (tan(sgn(x)))/(sgn(x))` if exists.
View SolutionIf `f(x)={(sinx, x != npi " and " n in Z), (2, " x=npi):}` and `g(x)={(x^2+1, x != 0),(4,x=0), (5, x=2):}` then `lim_(x->0) g{f(x)}` is
02:57View Solution
Exercise 2.1 questions and complete solutions for chapter LIMITS of CENGAGE of Class 12
All Exercises from CENGAGE NEW Class 12 MATHS LIMITS
- Comprehension Type
- ComprehensionType
- Examples
- Exercise (Comprehension)
- Exercise (Matrix)
- Exercise (Multiple)
- Exercise (Numerical)
- Exercise (Single)
- Exercise 2.1
- Exercise 2.2
- Exercise 2.3
- Exercise 2.4
- Exercise 2.5
- Exercise 2.6
- Exercise 2.7
- Exercise 2.8
- JEE Advanced Previous Year
- JEE Main Previous Year
- Multiple Correct Answer Type
- Multiple Correct Answers Type
- Question Bank
- Single Correct Answer Type
