Complete Solutions to Exercise of chapter GRAPHICAL TRANSFORMATIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | GRAPHICAL TRANSFORMATIONS |
| CENGAGE NEW | Exercise |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
Draw the graph of `y=tan^(-1)x-cot^(-1)x`.
View SolutionDraw the graph of `y=|(1)/(|x|)-2|`.
View SolutionDraw the graph of `y=tan^(-1)x+cos^(-1)x+sin^(-1)x`.
View SolutionDraw the graph of `|y|=(x-1)(x-2)(x-3)`.
View SolutionDraw the graph of `y=2sin^(-1)(x//3)`.
View SolutionDraw the graph of `y=cot^(-1)|x|`.
View SolutionDraw the graph of `y=sec^(-1)|x|`.
View SolutionDraw the graph of `y=|log_(e)(x+3)|`.
View SolutionDraw the graph of `y=|log_(e)|x||`.
View SolutionDraw the graph of `y=|{x}-0.5|`, where `{.}` represents the fractional part function.
View SolutionDraw the graph of `y=|sinx|+sin|x|`.
View SolutionIf the graph of `y=|f(x)|` is as shown in figure
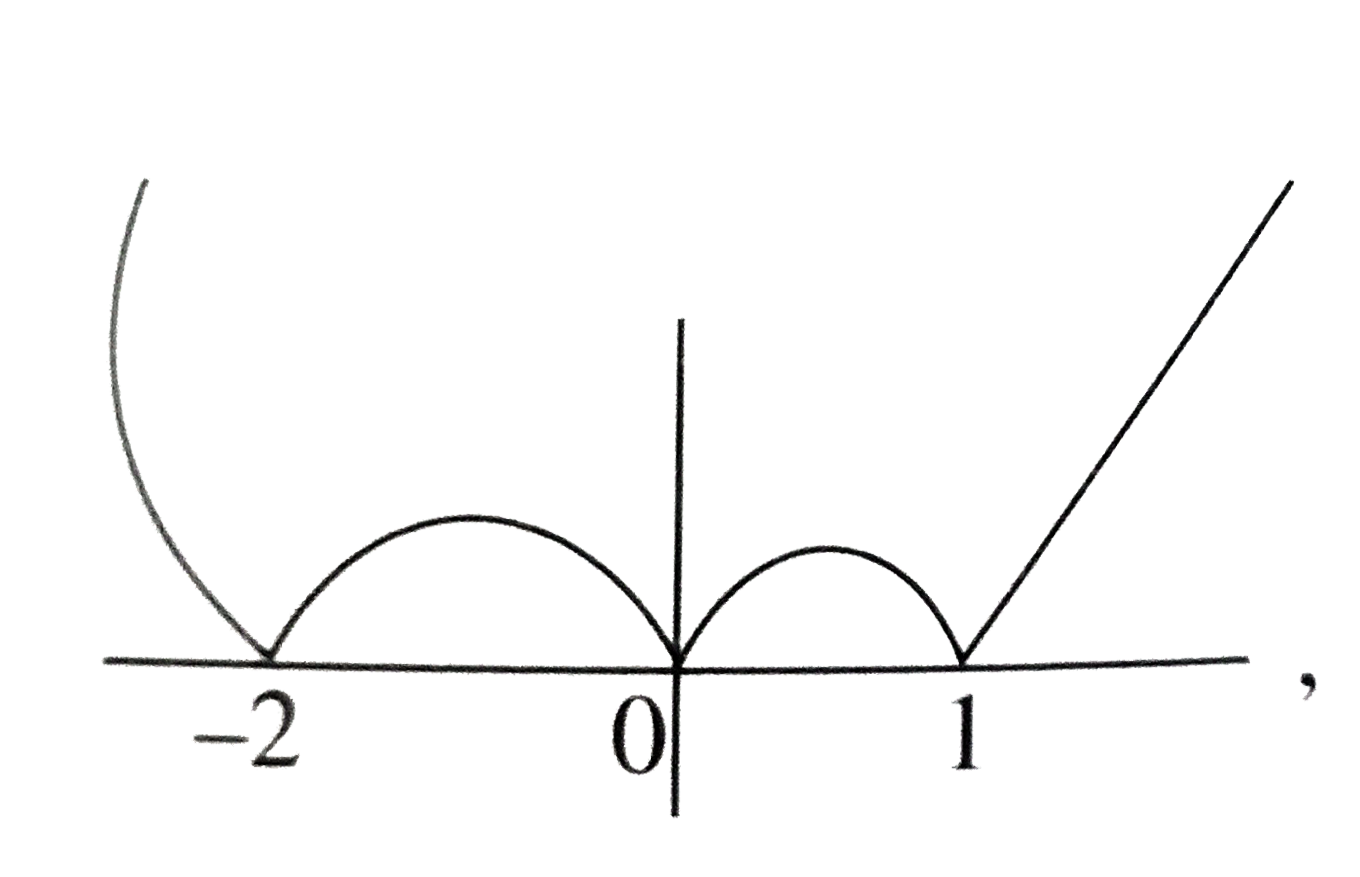 then the graph of `y=f(x)` may be
then the graph of `y=f(x)` may be
View SolutionThe number of real solutions of the equation `sqrt(1+cos2x)=sqrt(2)sin^(-1)(sinx),-pilt=xlt=pi` is 0 (b) 1 (c) 2 (d) infinite
View SolutionFind the number of real solutions to the equation `log_(0.5)|x|=2|x|`.
View SolutionFind the number of points where the function `f(x)=max|tanx|,cos|x|)` is non-differentiable in the interval `(-pi,pi)`.
View SolutionFind the number of points of non-diferentiability for `f(x)=max{||x|-1|,1//2}`.
View SolutionLet `f(x) = max. {|x^2 - 2| x ||,| x |}` then number of points where `f(x)` is non derivable, is :
View SolutionDraw the graph of `|y|=[x]`, where [.] represents the greatest integer function.
View SolutionDraw the graph of `|2x|+|y|=2` using graphical transformation.
View SolutionConsider the function `f(x)={2x+3, x le 1 and -x^2+6, x > 1` Then draw the graph of the function `y=f(x), y=f(|x|), y=|f(x)|, and y=|f(x)|.`
View SolutionThe graph of `y=f(x)` is as shown in the following figure. Draw the graph of `y=[f(x)]`.
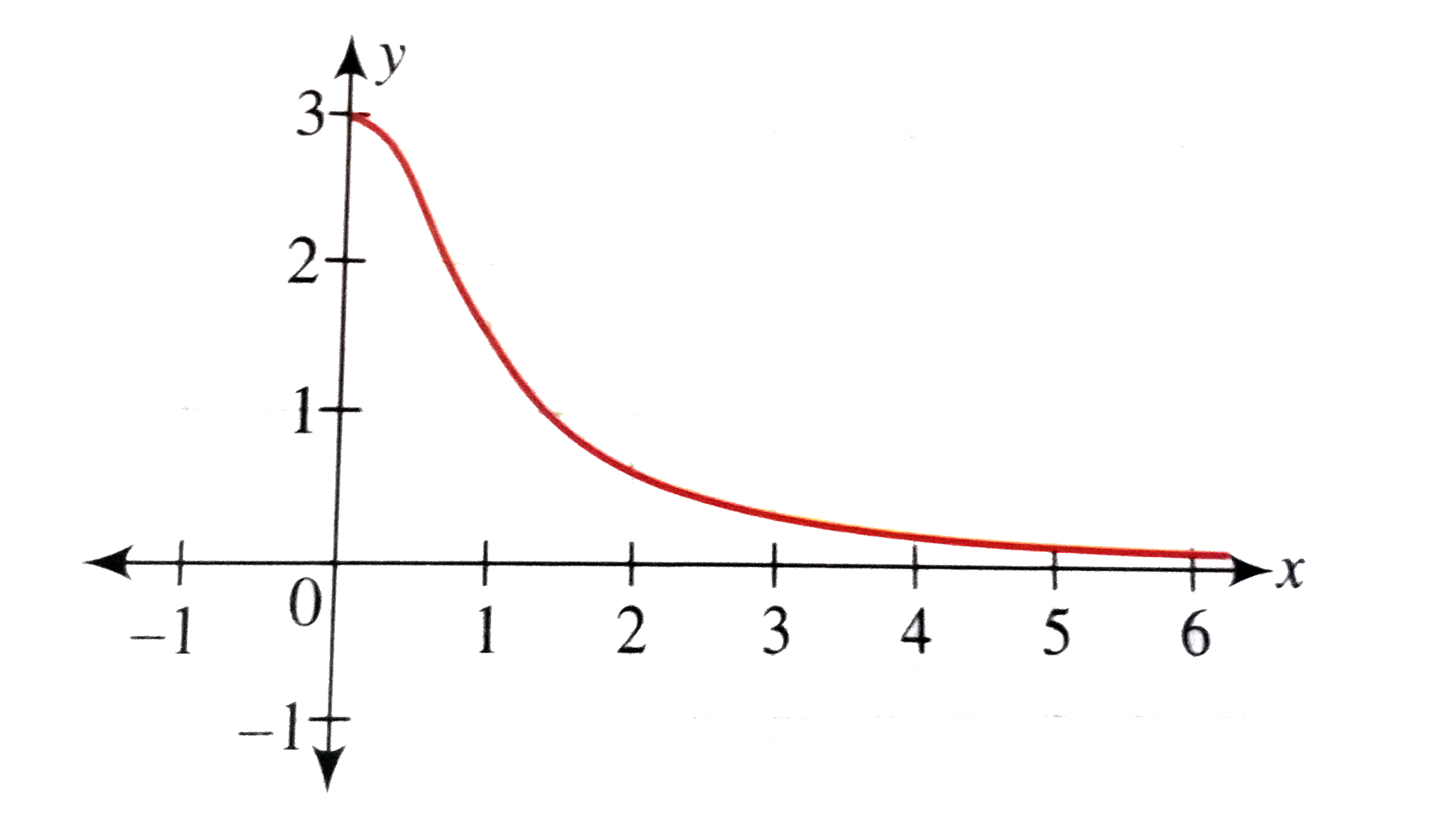
View SolutionDraw the graph of `y=[4-x^(2)],|x|le2`, where `[.]` represents the greatest integer function.
View Solution
Exercise questions and complete solutions for chapter GRAPHICAL TRANSFORMATIONS of CENGAGE MATHS (HINGLISH) of Class 12