Complete Solutions to JEE Advanced Previous Year of chapter INVERSE TRIGONOMETRIC FUNCTIONS of Class 12 book with complete answers and questions
| Class 12 | MATHS |
| Chapter | INVERSE TRIGONOMETRIC FUNCTIONS |
| CENGAGE NEW | JEE Advanced Previous Year |
| Number Of Questions | 8 |
| Academic Year | 2023-24 |
The value of `cot (sum_(n=1)^(23) cot^(-1) (1 + sum_(k=1)^(n) 2k))` is
04:05View SolutionIf `alpha=3sin^-1(6/11) `and `beta=3cos^-1(4/9)`, where the inverse trigonometric functions take only the principal values, then the correct option(s) is (are)
05:25View SolutionFor any positive integer `n` , define `f_n :(0,oo)rarrR` as `f_n(x)=sum_(j=1)^ntan^(-1)(1/(1+(x+j)(x+j-1)))` for all `x in (0, oo)` . Here, the inverse trigonometric function `tan^(-1)x` assumes values in `(-pi/2,pi/2)dot` Then, which of the following statement(s) is (are) TRUE? `sum_(j=1)^5tan^2(f_j(0))=55` (b) `sum_(j=1)^(10)(1+fj '(0))sec^2(f_j(0))=10` (c) For any fixed positive integer `n` , `(lim)_(xrarroo)tan(f_n(x))=1/n` (d) For any fixed positive integer `n` , `(lim)_(xrarroo)sec^2(f_n(x))=1`
09:17View SolutionMatch the statements in List I with those in List II
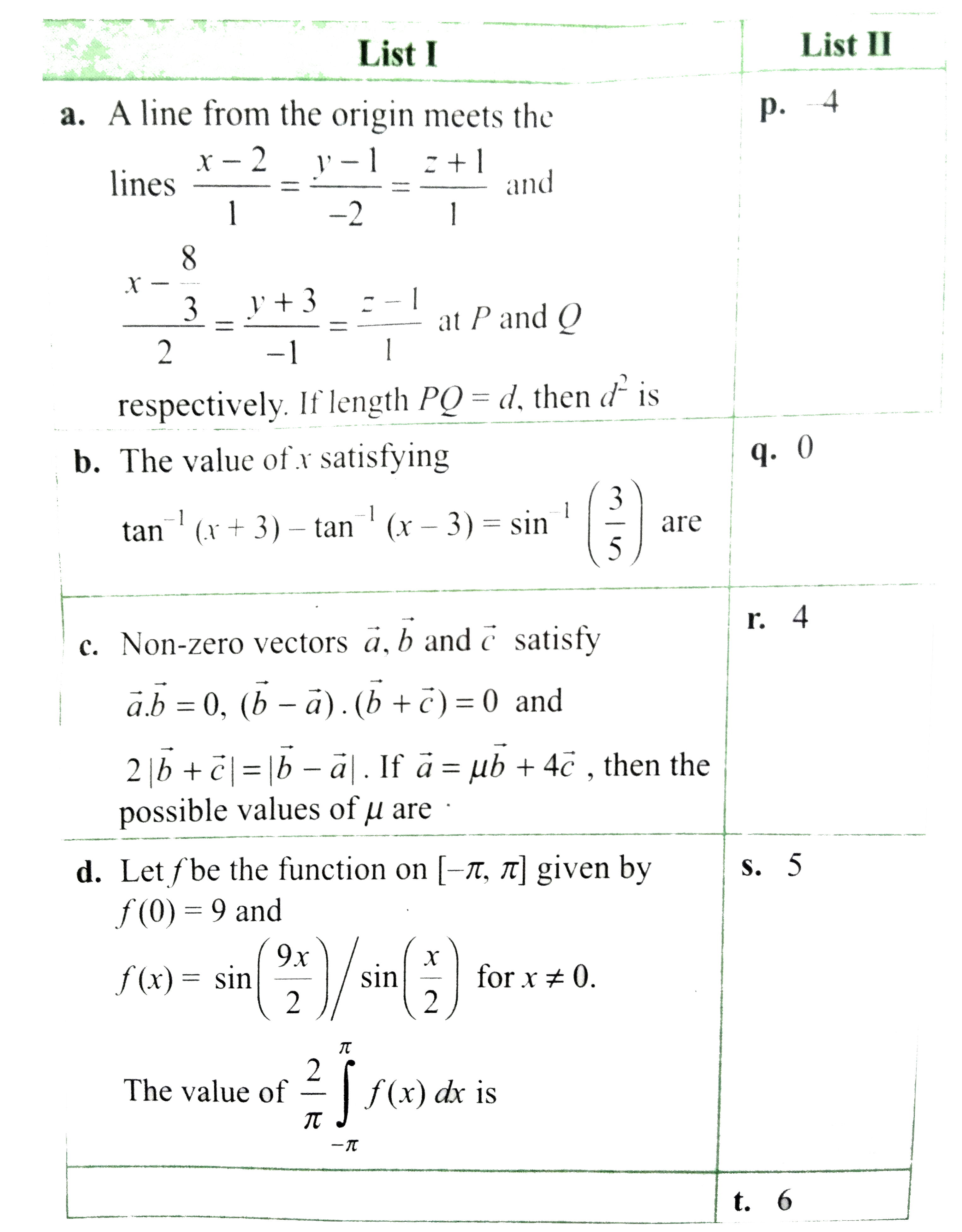 View Solution
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists:
 21:05View Solution
21:05View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :
 View Solution
View SolutionLet `f:[0,4pi]->[0,pi]` be defined by `f(x)=cos^-1(cos x).` The number of points `x in[0,4pi]` 4satisfying the equation `f(x)=(10-x)/10` is
03:18View SolutionThe number of real solution of the equation
`sin^(-1) (sum_(i=1)^(oo) x^(i +1) -x sum_(i=1)^(oo) ((x)/(2))^(i))`
`= (pi)/(2) - cos^(-1) (sum_(i=1)^(oo) (-(x)/(2))^(i) - sum_(i=1)^(oo) (-x)^(i))` lying in the interval `(-(1)/(2), (1)/(2))` is ______.
(Here, the inverse trigonometric function `sin^(-1) x and cos^(-1) x` assume values in `[-(pi)/(2), (pi)/(2)] and [0, pi]` respectively)08:16View Solution
JEE Advanced Previous Year questions and complete solutions for chapter INVERSE TRIGONOMETRIC FUNCTIONS of CENGAGE MATHS (HINGLISH) of Class 12
